被小船创飞了
众所周知,高中物理有一道很经典的分解速度的题:
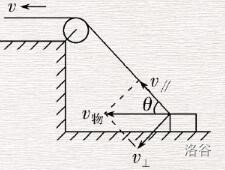
物理老师在上课讲这个题的时候,将速度分解为两个正交的速度,这两个速度的矢量和就是原速度.
乍一看好像非常合理,然而随即大家可能就会见到这个题:
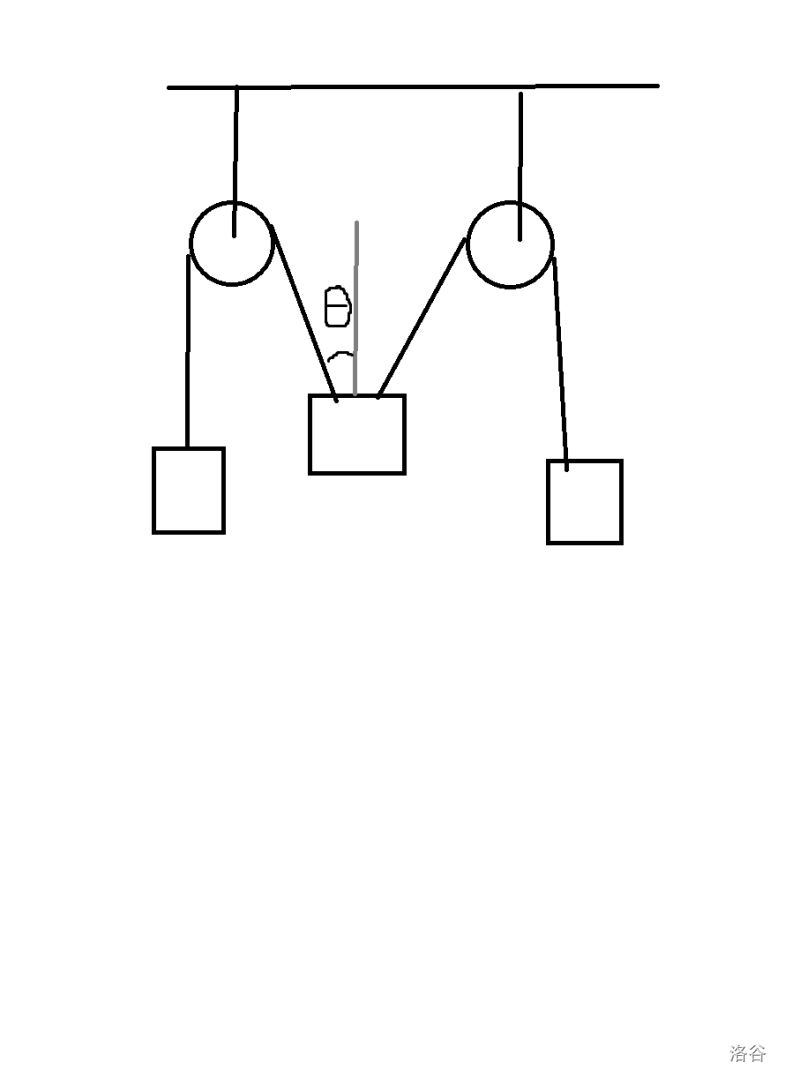
其中中间的物体下落的速度为\(v\),这个时候沿绳子分解速度的时候,两个分速度应该均是\(v\cos \theta\),而这个时候两个速度的矢量和并不是原速度啊!
老师讲到这里的时候,往往会说这是因为:“速度的分解和力的分解并不一样.”但你可能会疑问:同样是矢量的分解,为什么会不一样呢?
先提前给出我的思考:在这个滑轮组模型中,我们做的操作并不是将原速度分解为了这两个速度,这两个速度也并非由原速度一下分解出来的,而分别只是原速度分解出的速度的一部分.
先看这个最经典的模型:

不妨设高度差为\(h\),此时绳子长度为\(L\),物体距离墙的距离为\(x\).
有勾股定理: \(L^2=h^2+x^2\),注意到此时\(h\)是一个常量.
两边对\(t\)求导,自然有:
\[ 2Lv_L=2xv_x\\ v_L=\frac{x}{L}v_x=v_x\cos \theta \]
此时的另一个分速度自然是\(v_h=v_x\sin \theta\).在物理课上,物理老师会这么解释这种分解:
\(v_L\)这个速度提供了绳子缩短的速度,而\(v_h\)提供了绳子转动的速度.
那么这个\(v_h\)听上去应该是此时绳子与物体接触点的转动的线速度对吧.也就是说角速度应该是\(\omega=\frac{v_h}{L}=\frac{h}{L^2}v_x\),令绳子与转轴夹角为\(\alpha,\sin \alpha=\frac{x}{L}\)而我们有:
\[ \omega=\frac{\text d\alpha}{\text d t}\\ =\frac{\text d \alpha}{\text d \sin \alpha}\frac{\text d \sin \alpha}{\text d t}\\ =\frac{1}{\frac{\text d \sin \alpha}{\text d \alpha}}\frac{\text d \sin \alpha}{\text d t}\\ =\frac{1}{\cos \alpha}\frac{v_xL-v_Lx}{L^2}\\ =\frac{h}{L^2}v_x \]
这就证明了\(v_h\)的确是线速度,这也与我们直观感受相当匹配.
解释完上面这个分解的正确性,我们又要开始考虑了:那么为什么力和速度的分解不一样呢?
有一个很形象的比喻,那就是如果两个人同时以速度\(v\)的速度拉一个物体,这个物体的速度是\(v\);但如果两个人同时以力\(F\)拉一个物体,这个物体的受力是\(2F\).
这是为什么呢?动量定理实际上将力在时间上的积累与动量等价起来了对吧,由于速度并非是动量,因此自然像力那样叠加.这么思考也许是正确的:两个受力均为\(F\)的物体的合力是\(2F\),两个速度均为\(v\)的物体合速度为\(v\),两个动量均为\(p\)的速度相同的物体合动量为\(2p\).
或者换而言之,力的作用之间是有牛顿第三定律作保证的,这就可以让力在物体间存在一种类似传递的效果.但是速度并没有这种效果,速度并非是外界对物体做出的改变,而是物体的性质本身.
从这个角度,我们回到滑轮的那个题,我们就可以明白为什么要这么分解了:原因很简单,这两个沿绳的速度并不是一次分解分解出来的,而是让原本的速度先沿其中一个绳分解为两个速度,一个是沿绳的速度\(v\cos \theta\),另一个是提供绳转动的线速度\(v\sin \theta\).
而速度是不能叠加的,因此右边也做这个操作,这就使得沿绳的分速度均为\(v\cos \theta\).
回看开头的那个滑轮题,这题其实还有个很好玩的地方:那就是C的动能最大点可不是C的受力平衡点:原因很简单,C的受力平衡点由于滑轮作用仍然存在角速度上的加速度.