被摆球创飞了
今晚学弟问了我这么一个问题:
对于一个圆锥摆,设其绳上拉力为\(T\),我们有:
\[ T\sin\theta=m\omega^2\sin\theta L \\ T=m\omega^2L \]
那么问题来了:当小球自然下垂的时候,\(T=mg\),但是\(\omega=0\),左边不等于右边???
怎么处理这个问题呢?
下面是我个人的想法啊,不一定正确.
冷静一下,\(\omega=\frac{v}{r}\),我们的确能确认自然下垂的时候\(v=0\),但由于\(r\)也是\(0\),我们没道理判定\(\omega=0\).
那么我们把角速度换成线速度就有:
\[ T\sin\theta=m\frac{v^2}{\sin\theta L}\\ T\sin^2\theta=\frac{mv^2}{L} \]
这样极限情况下两边就相等了(均为\(0\)).
或者说我们还可以这么干:
考虑\(T=\frac{mg}{\cos\theta}\),所以\(\omega^2=\frac{g}{L\cos\theta}\),注意到其实\(\omega\)是随着小球下落而单调递减的,但是不可能减到\(0\).
另一个想法是:考虑先放一个实体圆锥(可提供支持力),让球在圆锥上转圈,然后逐渐加速到支持力\(N=0\),此时小球会飘起来.我们观察一下这个式子是啥:
考虑引入离心力,只需要让离心力,重力,支持力和拉力四力平衡即可,设绳子与竖直方向的夹角为\(\theta\),作正交分解后立刻有:
\[ \begin{cases} N\cos\theta=T\sin\theta-m\omega^2L\sin\theta\\ N\sin\theta=mg-T\cos\theta \end{cases} \]
替换掉其中的\(N\),得到:
\[ mg\cos\theta-T\cos^2\theta=T\sin^2\theta-m\omega^2L\sin^2\theta\\ T=mg\cos\theta+m\omega^2L\sin^2\theta \]
考虑\(T\)和\(\omega^2\)的函数关系,小球从在圆锥摆上的状态到飘起来的状态应该是连续的两段直线,注意到当\(\theta\rightarrow 0\)的时候,它俩的关系是\(T=mg\)的平行于\(\omega^2\)轴的直线,这段直线会一直延伸到\(\omega\)的最低点,也就是\(\omega=\sqrt{\frac{g}{L}}\)的点然后再转上去.
如果这个文章就这么结束还是有点无聊,不如让我们来看个类似的问题: 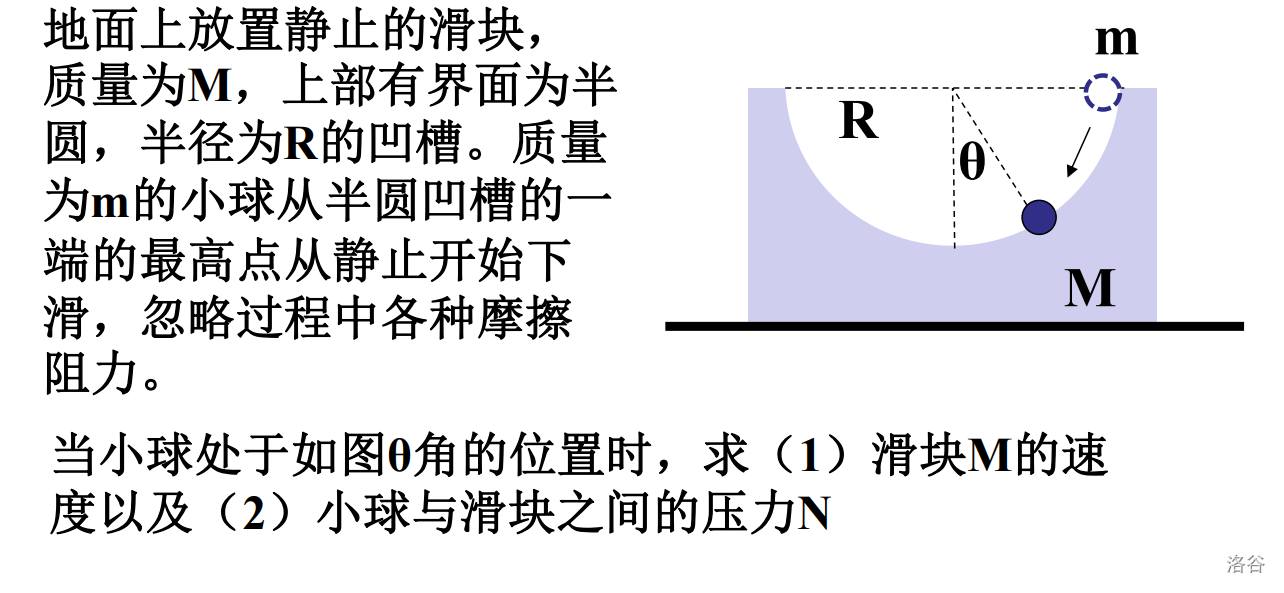
先来看第一问:
设水平向左为正方向,设小球相对于滑块的水平速度为\(v_1\),滑块速度为\(v_2\).
水平方向动量守恒,当然有\(m(v_1-v_2)=Mv_2\).
此时小球的总速度应该为\(v=\sqrt{(v_1-v_2)^2+(\frac{v_1\sin\theta}{\cos\theta})^2}=v_2\sqrt{(\frac{M}{m})^2+\frac{(M+m)^2\sin^2\theta}{m^2\cos^2\theta}}\).
小球和滑块的总机械能守恒,当然有:\(\frac{1}{2}mv^2+\frac{1}{2}Mv_2^2=mgR\cos\theta\).
两式联立,解得:\(v_2=\sqrt{\frac{2m^2gR\cos\theta}{(Mm+M^2)+(M+m)^2\tan^2\theta}}=\sqrt{\frac{2m^2gR\cos^3\theta}{(m+M)(M+m\sin^2\theta)}}\).
看上去只是麻烦而已,也没那么难嘛.
再来看第二问:
考虑\(a_n=\frac{(\frac{v_1}{\cos\theta})^2}{R}=\frac{v_2^2(M+m)^2}{m^2R\cos^2\theta}=\frac{2g(M+m)\cos\theta}{M+m\sin^2\theta}\),
而滑块的水平加速度大小应该是\(a'=-\frac{N\sin\theta}{M}\),那么惯性力\(F'=-a'm=\frac{mN\sin\theta}{M}\).
而\(a_nm=N-mg\cos\theta+F'\sin\theta\),\(\frac{M+m\sin^2\theta}{M}N=ma_n+mg\cos\theta=\frac{2gm(M+m)\cos\theta}{M+m\sin^2\theta}+mg\cos\theta=mg\cos\theta(\frac{3M+2m+m\sin^2\theta}{M+m\sin^2\theta})\),整理得到\(N=Mm\cos\theta(\frac{3M+3m-m\cos^2\theta}{(M+m\sin^2\theta)^2})\).方向沿半径方向朝向圆心.
这里就要用惯性力了.