简单乐理

前言

这个博客是北京大学课程《音乐与数学》的相关笔记.然而我懒得画五线谱以及插入钢琴图片,所以这里我们只空谈理论.

本人在大学前并未学过相关乐理,所以下面的个人理解当然可能会出错.

泛音列

拍音理论

假设两个正弦单音的频率分别是$\omega , \omega + \delta$,那么它们叠加后是:

$$\begin{aligned} & \sin ( 2 \pi ( \omega + \delta ) t ) + \sin ( 2 \pi \omega t ) \\ = & 2 \sin \left ( 2 \pi ( \omega + \frac{ \delta }{ 2 } ) t \right ) \cos ( \pi \delta t ) \end{aligned}$$

注意到这个声音受到$\cos ( \pi \delta t )$的控制.因此会以$\frac{ \delta }{ 2 }$的频率振动,由于$\delta$应该远小于$\omega$,这里就会产生$\delta = | \omega_1 - \omega_2 |$个拍音.

Mersenne定律

考虑弦乐的情况,将一根弦理想化后,可以只关注它的三个参数:

1. 弦长$L$.

2. 张力$T$.

3. 线密度$\rho$.

对于弦的振动解微分方程,这里我不是很想解了啊!所以我们直接放结论,对于弦上一个点$u ( x , t )$,首先是一维振动方程:

$$\frac{ \partial^2 u }{ \partial x^2 } = \frac{ \rho }{ T } \frac{ \partial^2 u }{ \partial t^2 }$$

最终得到的会是一个无穷级数,这个无穷级数的每一项都形如:

$$u_n ( x , t ) = c_n \sin ( \omega_n t + \theta_n ) \sin ( \frac{ n \pi }{ L } x )$$

其中第$n$项的频率满足:

$$f_n = \frac{ n }{ 2 L } \sqrt{ \frac{ T }{ \rho } }$$

其中我们将$f_1$称为基频,相应的声音称为基音,而将剩下的频率对应的声音统称为泛音,其中$f_n , n \geq 2$对应的是第$n - 1$泛音.

特别地,如果我们干脆记$f = f_1$,上述结果告诉我们弦的振动产生的一列频率是:

$$f , 2 f , 3 f , \cdots$$

这个序列通常被称为泛音列.

特别地,上述的频率其实是固定了点来讨论的,实际上的泛音要更为复杂,会在一根弦上的不同位置处产生不同的加权.实际上对于不同的$n$,它们的泛音列长这个样子: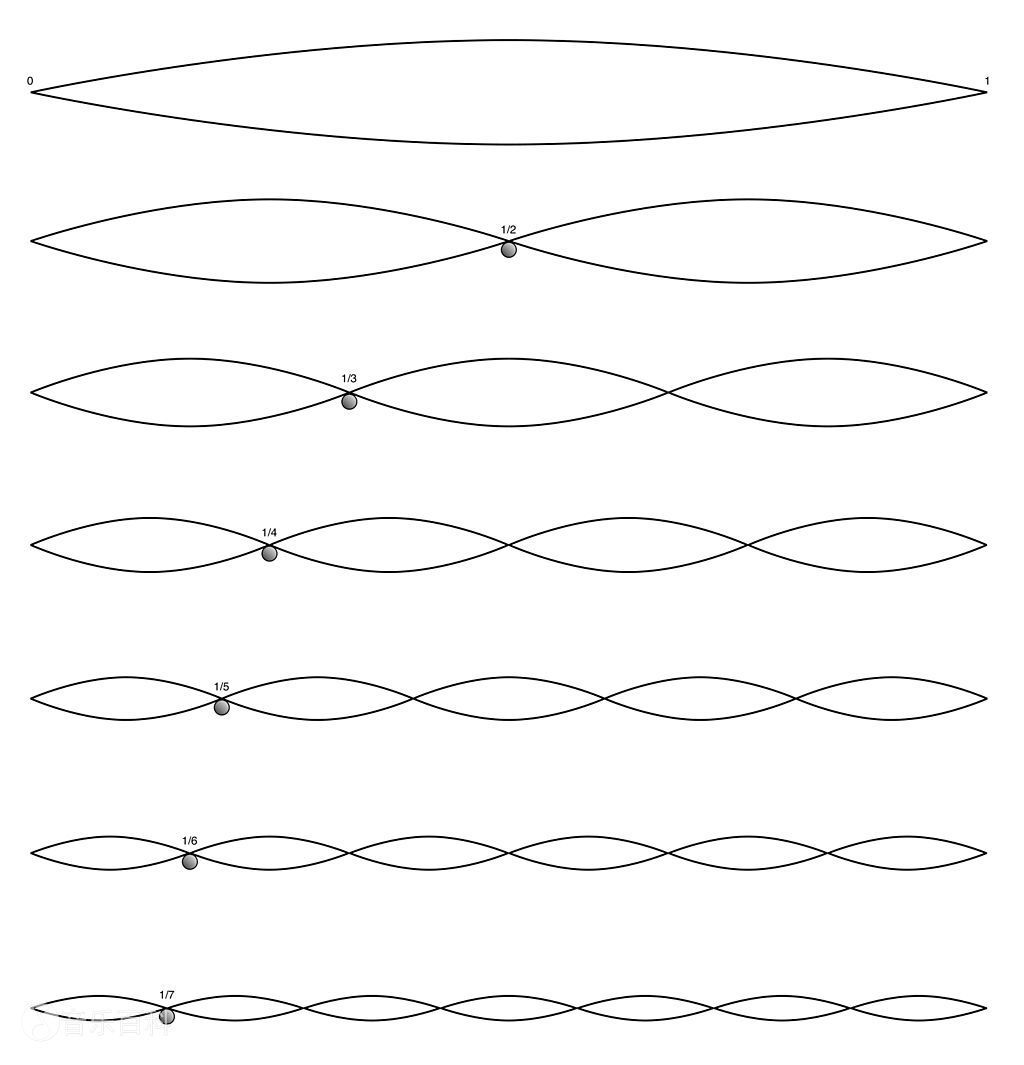

其中标注的点(波节)在振动中均是固定不变的.

这其实是某些弦乐演奏中一些按弦技巧的基础.例如这里,如果我用手轻触中间点,我就可以消灭掉所有的$f_{ 2 k + 1 }$,泛音列中只剩下$2 f , 4 f , \cdots$.我们后面会再提这个事,这意味着我弹出的音高了八度.那如果我按$\frac{ 1 }{ 3 }$处呢?那泛音列中就会只剩下$3 f , 6 f , 9 f , \cdots$,也就是先高一个纯八度,再高一个纯五度.

还有拨弦,如果我在中间拨弦会发生什么呢?由于我的拨动使得整个弦应该以中间为对称形成一个偶函数,中间的点一定在波动,因此泛音列中剩下的就会是$f , 3 f , 5 f , \cdots$.

管乐器

管乐器中振动的变为空气柱,不过吧空气柱这个东西振动的时候会略微超出管口,因此会有管口矫正这个事存在.

再就是,管乐器其实分为两种:开管(两面开口)和闭管(单面开口).而且不像琴弦的两端是固定的.一个自然的想法是,根据上面我们放的那张图,开口的那个位置一定要振动,而闭口的那个位置一定被卡住不动.这意味着开管和闭管的泛音列天然不同.具体来说:

开管的泛音列:

$$f , 2 f , 3 f , 4 f , \cdots$$

闭管的泛音列:

$$f , 3 f , 5 f , 7 f$$

另外,相同长度的管,开管的基音比闭管高了一个八度.

管乐器有一种演奏方式是超吹.简单来说,当你用力吹的时候,直觉上随着你用力越大,你吹出来的音的频率应该是连续的.但实际上听感更接近于离散的.这是因为从一开始整个泛音列就都是存在的,只是当气流加快的时候,后面的音在某种程度上被”加强”了,所以对于开管来说,你会先听到一个高八度的音,再听到一个高五度的音.

泛音列重合理论

既然如此,我们可以见到,当两个音的基频的比较为简单的时候,它们产生的泛音列重合程度就会较高.例如:

$$\begin{gathered} f , 2 f , 3 f , 4 f , \cdots \\ 2 f , 4 f , 6 f , 8 f , \cdots \end{gathered}$$

或是:

$$\begin{gathered} f , 2 f , 3 f , 4 f , \cdots \\ \frac{ 3 }{ 2 } f , 3 f , \frac{ 9 }{ 2 } f , 6 f , \cdots \end{gathered}$$

这从相当的程度解释了为什么理想的音程全都是简单整数比.

律制

要讲律制,首先要知道从经验上来讲,人耳对于音乐的听觉其实并非线性.换言之,当你听两个音的时候,你关注的可不是它们之间的频率差值,而可能更关注它们之间的频率比值.类似地,其实人听声压的时候靠的也是比值,例如分贝的定义是$L_p = 20 \log_{ 10 } ( \frac{ p }{ p_0 } )$,其中$p_0 = 20 \mu Pa$.

音程

我们称两个音级之间的距离为音程,其中高的音称为冠音,而低的音被称为根音,一个音程应该由两个参数决定:度数和半音数,简单来说,度数是跨越的音名数量,而半音数是跨越的半音数量.表格长这样:

| 度数 | 半音数 | 名称 |

| —— | ——— | ——— |

| 一 | 0 | 纯一度 |

| 二 | 1 | 小二度 |

| 二 | 2 | 大二度 |

| 三 | 3 | 小三度 |

| 三 | 4 | 大三度 |

| 四 | 5 | 纯四度 |

| 四 | 6 | 增四度 |

| 五 | 6 | 减五度 |

| 五 | 7 | 纯五度 |

| 六 | 8 | 小六度 |

| 六 | 9 | 大六度 |

| 七 | 10 | 小七度 |

| 七 | 11 | 大七度 |

| 八 | 12 | 纯八度 |

从这套理论出发,毕达哥拉斯说我们找一下最简整数比:注意到:

| 音程 | 频率比 |

| ——— | ——— |

| 纯八度 | $2 : 1$ |

| 纯五度 | $3 : 2$ |

| 纯四度 | $4 : 3$ |

| 大三度 | $5 : 4$ |

| 小三度 | $6 : 5$ |

看上去太漂亮了对吧!但是就是这个规定出了大锅.

五度相生律

中国的三分损益法和毕达哥拉斯的五度相生法其实是类似的东西,我们这里只考虑五度相生律.

毕达哥拉斯学派说,我们这么干,规定$C$的频率(当时其实不存在频率的概念,但我们这里就为了方便这么说了)为$1$,然后每次向上升一个纯五度,如果超出去了呢,那就降一个八度降回来.回忆到纯五度是七个半音,这相当于求$\{ 7 k \} \pmod{ 12 }$这个数列对吧,简单数论知识告诉我们它必然能遍历$12$种情况,具体而言:

$$\begin{aligned} C \to & & G \to & & D \to & & A \to & & E \to & & B \to \\ 1 \to & & \frac{ 3 }{ 2 } \to & & \frac{ 3^2 }{ 2^3 } \to & & \frac{ 3^3 }{ 2^4 } \to & & \frac{ 3^4 }{ 2^6 } \to & & \frac{ 3^5 }{ 2^7 } \to \\ \\ \\ \# F \to & & \# C \to & & \# G \to & & \# D \to & & \# A \to & & \# E \\ \frac{ 3^6 }{ 2^9 } \to & & \frac{ 3^7 }{ 2^{ 11 } } \to & & \frac{ 3^8 }{ 2^{ 12 } } \to & & \frac{ 3^9 }{ 2^{ 14 } } \to & & \frac{ 3^{ 10 } }{ 2^{ 15 } } \to & & \frac{ 3^{ 11 } }{ 2^{ 17 } } \\ \end{aligned}$$

我们是拿纯八度和纯五度生成的所有的音,因此纯五度肯定是准的,那么与之对应的纯四度肯定是准的.但是看三度音程就会发现问题,例如大三度$CE$的比是$\frac{ 81 }{ 64 } > \frac{ 80 }{ 64 } = \frac{ 5 }{ 4 }$.

更难过的是就算我们按照纯八度和纯五度生成的,这个纯八度也有点难绷.具体而言这里的$# E \ne F$,你对着这个$# E$往上再升一个音得到的理应是$C ‘ = \frac{ 3^{ 12 } }{ 2^{ 18 } } > 2$,具体来说$\frac{ 3^{ 12 } }{ 2^{ 19 } } \approx 1 . 013643$,这就出事了,这个东西转一圈并没有转到理想的纯八度音阶上,这个问题在中国古代的三分损益上也体现了,那里的名字叫旋宫不归,这里的话则是将这个略大于$1$的数叫做毕达哥拉斯音差.

仔细分析一下就会发现这个问题几乎是不可避免的,因为你上升$12$个纯五度,再下降$7$个纯八度理应回到原点,可是:

$$( \frac{ 3 }{ 2 } )^{ 12 } \times ( \frac{ 1 }{ 2 } )^7 > 1$$

这下这下了.

纯律

其实我们刚才就能见到真正完美符合简单整数比的律根本调不出来.但是能不能让一些常用的音程(比如纯八度,纯五度,纯四度,大三度)尽可能准呢.这就是纯律在干的事.

还是规定$C$的频率为$1$.接下来用正三和弦(一个大三度和一个小三度)$I : C - E - G$,$IV : F - A - C ‘$,$V : G - B - D ‘$的比例是$4 : 5 : 6$确定剩下的:

$$\begin{aligned} C & & D & & E & & F & & G & & A & & B & & C ' & & D ' \\ 1 & & \frac{ 9 }{ 8 } & & \frac{ 5 }{ 4 } & & \frac{ 4 }{ 3 } & & \frac{ 3 }{ 2 } & & \frac{ 5 }{ 3 } & & \frac{ 15 }{ 8 } & & 2 & & \frac{ 9 }{ 4 } \end{aligned}$$

所以现在大三度和小三度都准了.但问题又来了:

1. 五度音程$D - A$不协和,比例为$\frac{ 80 }{ 54 } < \frac{ 81 }{ 54 } = \frac{ 3 }{ 2 }$.这直接导致了转调会出错.

2. 有两种不同的大二度:音程$C - D , F - G , A - B$的比例是$\frac{ 9 }{ 8 }$而音程$D - E , G - A$的比例为$\frac{ 10 }{ 9 }$.

3. 谐调音差:从$C$出发升高四个纯五度,降低两个八度和一个大三度后,得到的是:$( \frac{ 3 }{ 2 } )^4 \times ( \frac{ 1 }{ 2 } )^2 \times \frac{ 4 }{ 5 } = \frac{ 81 }{ 80 } = 1 . 0125 > 1$.

十二平均律

既然我们一开始就说了律是根据比值来定的,为什么不直接简单一点,干脆用$\sqrt[12]{ 2 }$来平均律制呢?于是将近五百年前就有了朱载堉这位手开十二次根号的神人.这也是所有律法中几乎最简单的一种了,以至于我到这里发现没啥可写的了.

但它的问题也是最一眼能看出来的,那就是除了纯八度,全都不准.

先在这里定义音分的概念,设两个声音的频率分别是$f_1 , f_2$,则它们的音分数定义为$1200 \log_2 ( \frac{ f_2 }{ f_1 } )$,容易见到十二平均律拿到的一个半音恰好是$100$音分.

用音分可以迅速确定一下,发现十二平均律这玩意准的离谱,虽然哪里都差一点,但哪里差的都不多.

调式

大小调

自然大调

就是我们最常用的$CDEFGABC ‘$,用大二度和小二度组织调式.具体而言,以一个大二度分开了两组四声音阶(均为大大小),按顺序分别为:

1. 主音

2. 上主音

3. 中音

4. 下属音

5. 属音

6. 下中音

7. 导音

用五度相生,下属音$\rightarrow$主音$\rightarrow$属音.

自然小调

以一个大二度分开了两组四声音阶(分别为大小大和小大大)

以$ABCDEFG$用的调子,然而这里的问题是$G$作为导音却和$A ‘$差了个全音,导得不好.

和声小调

以一个大二度分开了两组四声音阶(分别为大小大和小增小)

将自然小调的导音升高一个半音.用$A , B , C , D , E , F , (^# G )$.

但是这样出了个增二度.

旋律小调

以一个大二度分开了两组四声音阶(分别为大小大和大大小)

把下中音也升上去,这样差的就小,用$A , B , C , D , E , (^# F ) , (^# G )$.

可以见到小调改音的主要目的是为了调导音的作用,这种作用只有在上行音阶的时候才是需要人为更改的,因此下行音阶不改音,与自然小调的下行音阶保持一致.

升降号调

以五度相生:

$$C \to G \to D \to A \to E \to B \to (^\# F ) \to (^\# C )$$

依次考虑它们为主调的自然大调音阶.

大调音阶的前后是对称的全全半+全+全全半结构,跳一个五度刚好能从前半部分跳到后半部分,因此从$C$开始每次往后跳一次都要在一个音阶上增一个升号.从$C$大调提升到$G$大调的时候就是将$C$的下属音(也就是$F$)升音.

对称地,反方向的五度相生:

$$C \to F \to (^b B ) \to (^b E ) \to (^b A ) \to (^b D ) \to (^b G ) \to (^b C )$$

那这个应该降什么呢?比如从$C$大调提升到$F$大调的时候就是将$F$的下属音$B$降一个音对吧.

所以最后的结果就是:

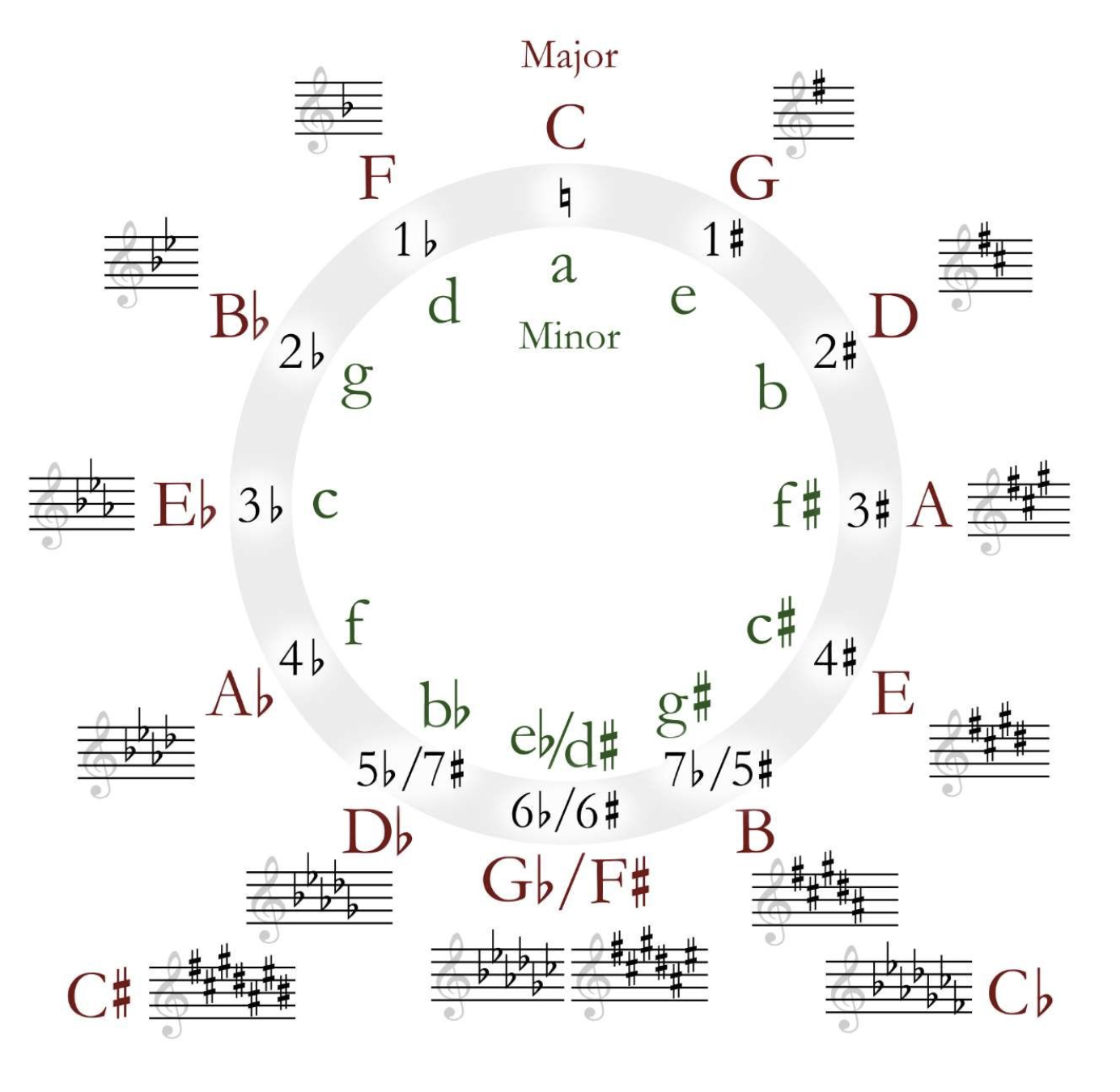
一个自然大调将主音向前挪小三度就得到了一个自然小调,它们称为一对关系大小调.

具有相同主音的大小调被称为平行大小调.其实也就是名字精确到大小写是一样的.

一个大调的下属音大调和属音大调以及对应的关系小调称为其近关系调.

和弦

三和弦

按照三度音程叠起来的三个音所构成的和弦被称为三和弦.其中最下面的音被称为根音,最上面的音被称为冠音或者五音,中间的被称为三音.

由于三度音程分大小,所以就有了四种不同的三和弦.

1. 大三和弦:下面一个大三度,上面一个小三度,刚好形成$4 : 5 : 6$的频率关系.

2. 小三和弦:下面一个小三度,上面一个大三度.

3. 减三和弦:两个小三度.

4. 增三和弦:两个大三度.

七和弦

按照三度音程叠四个音构成的和弦被称为七和弦.除去其中由三个大三度构成的(这样使得最上方的七音和最底下的根音形成了八度)以外,其余七种七和弦依照三和弦名称+七度音阶名称的原则命名,如下:

1. 减减七和弦(减七和弦):小小小.

2. 减小七和弦(半减七和弦):小小大.

3. 小小七和弦(小七和弦):小大小.

4. 小大七和弦:小大大.

5. 大小七和弦(属七和弦):大小小.

6. 大大七和弦(大七和弦):大小大.

7. 增大七和弦:大大小.

很遗憾的是七和弦全部包含至少一个不协和音程,所以它们全都是不协和和弦.

和弦转位

以根音为低音的和弦为原位和弦,以三五七音为低音的则称为转位和弦.

对于三和弦来说:

1. 以三音作为低音的称为第一转位,也称作六和弦.

2. 以五音作为低音的称为第二转位,也称作四六和弦.

对于七和弦来说:

1. 以三音作为低音的称为第一转位,也称作五六和弦.

2. 以五音作为低音的称为第二转位,也称作三四和弦.

3. 以七音作为低音的称为第三转位,也称作二和弦.

和弦的调性

在调式的主音,下属音,属音上的和弦分别被称为主和弦(I),下属和弦(IV),属和弦(V),它们被统称为正和弦,在C大调中体现为$C - E - G$,$F - A - C ‘$,$G - B - D ‘$.其中主和弦一般比较稳定,属和弦则比较飘渺,下属和弦往往则起到过度作用.

一定范围内的和弦连接被称为和声进行,下面是三种基本形式:

1. 正格进行:$I \to V \to I$.

2. 变格进行:$I \to IV \to I$.

3. 复式进行:$I \to IV \to V \to I$.

对于大调来说,其不同的三和弦之间有更加复杂的关系.经验给出以下图表:

$$\xymatrix{ & & & & I \\ & & IV \ar[r] \ar[d] \ar[dr] \ar[rru] & vii \degree \ar[ru] & \\ iii \ar[r] & vi \ar[r] \ar[ru] & ii \ar[r] \ar[ru] & V \ar[ruu] & }$$

其中$I$较为特殊,可以走向全部的和弦,这里略去不画.

新黎曼理论

引入以下三种对三和弦的变换(均会使得大和弦变小和弦,小和弦变大和弦):

1. 平行变换$P$:保持纯五度音阶不变,将三音切换.

2. 关系变换$R$:保持大三度音阶不变,补上剩下的一个(等价于大小调转换).

3. 导音变换$L$:保持小三度音阶不变,补上剩下的一个.

容易见到$R \circ ( L \circ R )^3 = P$.