被蝴蝶创飞了
事情是这样的,很久很久很久以前,我做了一个圆锥曲线压轴题,大概就是椭圆$x$轴上蝴蝶定理硬算题给我整傻眼了.今天我闲的没事乱想突然意识到椭圆可以仿射变换到圆来解决,那么圆肯定有很优美的做法了吧!
然而我瞪了半天也没看出来,没办法最后拿联消判韦把圆的结论搓出来了.
这个时候我又想看看其它的圆锥曲线,发现双曲线好像有点不太会,因为我不是很懂双曲线的内部是啥,然后我发现抛物线的蝴蝶定理更加优美.
所以我就把这一坨东西出了思考题,下面是整理.
约定
下文称$A , B , C$三点满足蝴蝶定理,当且仅当A,B,C三点都在圆锥曲线内部,并且过A的直线与圆锥曲线交于$P , Q$两点,$PB , QB$分别与圆锥曲线交于$P ‘ , Q ‘$两点,而且$P ‘ Q ‘$恒过$C$点.
抛物线
定理1
对于任何一条抛物线$y^2 = 2 px$以及与其内部一点$A ( a , 0 )$,过$A$点与抛物线相交的两个点的横坐标之积等于$a^2$.
证明:联立即可.
定理2
对于任何一条抛物线$y^2 = 2 px$以及其内部的三点$A ( a , 0 ) , B ( b , 0 ) , C ( c , 0 )$,三点满足蝴蝶定理当且仅当$b^2 = ac$.
证明:由定理1,我们有:
x_Qx_{Q’}=b^2\\x_{P’}x_{Q’}=c^2\end{cases}
简单解一下就可以.
定理3
对于任何一条抛物线$y^2 = 2 px$以及其内部的两点$A ( x_a , y_a ) , B ( x_b , y_b )$,要么存在一个点$C$使得$A , B , C$三点满足蝴蝶定理,要么$P ‘ Q ‘$的斜率恒定.
证明:
引理
如果一条动直线$Ax + By + C = 0$中,$A , B , C$满足一次方程$pA + qB + C = 0$,那么这条直线肯定过定点$( p , q )$.
而如果可以找到一个参数$t$,使得可以做到将$A , B , C$分别表示为$f ( t ) , g ( t ) , h ( t )$的形式,其中$f , g , h$都是关于$t$的一次函数或常函数,那么这条直线要么过定点,要么斜率恒定.
对于$P ‘ Q ‘$这条直线,这个$t$相当好找,可以是$k_{ PQ }$,可以是$y_P y_Q$,可以是$y_P + y_Q$,然后带入简单检验一下即可.
圆
定理(坎迪定理)
特例
对于任何一个圆$x^2 + y^2 = r^2$以及其内部三点$A ( a , 0 ) , B ( b , 0 ) , C ( c , 0 )$,若三点满足蝴蝶定理,当且仅当$( a + c ) ( b^2 + r^2 ) = 2 b ( ac + r^2 )$.
通解
对于任何一个圆,我们有下图(图源自百度百科)
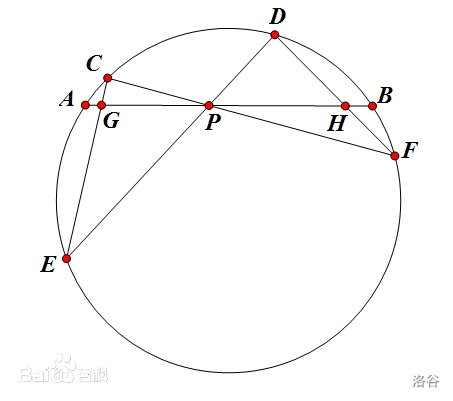
那么$\frac{ 1 }{ GP } - \frac{ 1 }{ HP } = \frac{ 1 }{ AP } - \frac{ 1 }{ BP }$.
该定理的几何/代数证明好像都略麻烦,笔者决定开摆
@Querainy 牛逼,下面给出他提供的曲线系证明:
我们尝试把这个做法拓展到坎迪定理上.
照葫芦画瓢,设圆心为$( x_0 , y_0 )$,得到$( CE , DF ) : ( 1 + \lambda k_1 k_2 ) x^2 - 2 x_0 x + x_0^2 + y_0^2 - r^2 = 0$.
此时,$| AB | = \sqrt{ r^2 - y_0^2 }$,$| AP | = | AB | - x_0 , | BP | = | AB | + x_0$,$\frac{ 1 }{ AP } - \frac{ 1 }{ BP } = \frac{ 2 x_0 }{ r^2 - y_0^2 - x_0^2 }$.
而$\frac{ 1 }{ GP } - \frac{ 1 }{ HP } = - \frac{ y_1 + y_2 }{ y_1 y_2 } = \frac{ 2 x_0 }{ r^2 - y_0^2 - x_0^2 }$.
笔者后来思考了一下为什么这个是二次曲线系啊.
我们考虑求过四个定点的二次曲线系,不妨假设这些二次曲线均为$Ax^2 + By^2 + Cxy + Dx + Ey + F = 0$\\
带入四个定点坐标,就可以得到关于$( A , B , C , D , E , F )$的四个方程.不妨先假设这四个方程线性无关.那么就有两个自由元,那么方程的任何一个解,就可以表示为两组线性无关的特解的线性组合.
注意到两个二次曲线线性相关,当且仅当它们是同一条曲线,这就证明了二次曲线系的正确性!
那么怎么证明这四个方程线性无关呢,不太会啊,这次真摆了.
椭圆
定理1
对于任何一个椭圆$\frac{ x^2 }{ r^2 } + \frac{ y^2 }{ d^2 } = 1 ( r > d )$以及其内部三点$A ( a , 0 ) , B ( b , 0 ) , C ( c , 0 )$,若三点满足蝴蝶定理,当且仅当$( a + c ) ( b^2 + r^2 ) = 2 b ( ac + r^2 )$.
证明:
注意到圆的坎迪定理的特例,然后发现我们如果将椭圆的纵轴拉长使其成为一个圆,换言之就是对椭圆进行仿射变换,那么$A , B , C$三点坐标不变并且仍然满足蝴蝶定理.
其它
众所周知,极点极线有一个经典内切四边形结论,其实也就是所谓的完全四边形啊.
给张图,
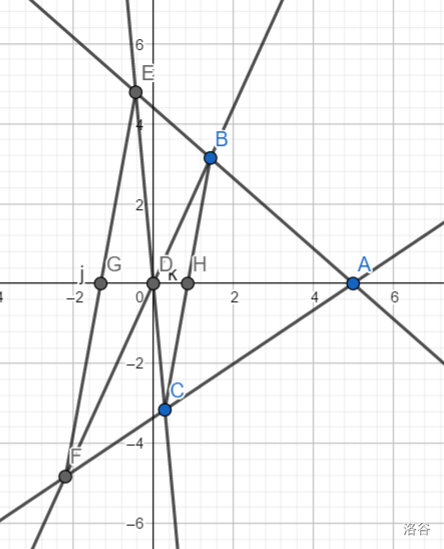
其中$G , D , H , A$成调和点列.
我们冷静一下,注意到$( AF , AE )$就是一个二次曲线,而且$F , C , B , E$是二次曲线上四个点,所以这个还可以用曲线系方程来证明这四个点成调和点列,非常有实力.
当然,为了应对文化课,我们有更加简单的证明完全四边形调和点列的做法:
不妨设$d = \frac{ BC }{ EF }$,令$\vec{ e } = \vec{ AE } , \vec{ f } = \vec{ AF }$,则$\vec{ AD } = \lambda_1 \vec{ e } + \mu_1 d \vec{ f } = \lambda_2 d \vec{ e } + \mu_2 \vec{ f }$,对比系数得到两个方程,再加上$\mu_1 + \lambda_1 = 1 , \mu_2 + \lambda_2 = 1$,立刻解出结论.