LWLAymh的备忘录

高等代数

发表于 2025-06-23 更新于 2025-11-13 分类于大学课程 Waline：

抽象代数
线性代数

阅读全文 »

递归式与和式

发表于 2025-06-23 分类于具体数学 Waline：

汉诺塔问题

三个柱子,$n$个面积互不相等的有孔圆盘一开始按照面积从上往下以此增大的顺序套在其中一个柱子上.

现在每次可以将某根柱子顶端的圆盘移动到另一根柱子顶端,要求这根柱子原本没有圆盘或者柱子顶端圆盘面积大于该圆盘.

求最小移动次数,使得所有圆盘移动到另一根柱子上.

不妨令$T_n$表示答案,显然$T_0 = 0 , T_1 = 1$.

而我们一定可以找到一种方案,使得前$n - 1$个圆盘先移动到其中一根柱子上,然后将最下面的圆盘移动到目标柱子,最后再把$n - 1$个圆盘移动到目标柱子.由于这是一个可行解而不一定是最优解,我们有:$T_n \leq 2 T_{ n - 1 } + 1$.

而如果我们要移动最大的圆盘,一定要保证前n-1个圆盘已经移走到一根柱子上.因此一定有:$2 T_{ n - 1 } + 1 \leq T_n$.于是有$T_n = 2 T_{ n - 1 } + 1$.

Example1(《具体数学》1.2)

汉诺塔问题,所有圆盘一开始均在最左边的塔A上,要将他们全都移动到最右边的塔C上,不允许在二塔之间直接移动,求最小操作次数.

Solution 1

考虑设$T_n$为n个圆盘时的最小操作次数.假设已知$T_{ n - 1 }$,我们考虑如何移动.

首先因为不能直接在AC之间移动,因此一定是先要把最大的圆盘移动到中间塔上,这一步要求先把所有圆盘移动到C上,然后需要再把这些圆盘移动回A上,因此,显然有:$T_{ n } = 3 T_{ n - 1 } + 2 , T_0 = 0$.

考虑如何求该式子的封闭形式,令$W_n = T_n + 1$,显然有$W_n = 3 W_{ n - 1 } , W_0 = 1$,显然$W_n = 3^n$,有$T_n = 3^n - 1$.

注意到$T_n$刚好是三根柱子上所有合法排列的数量,并且这个过程中不可能出现某两个时刻的情况是相同的,因此1.3也可以证明.

Example2(《具体数学》1.4)

汉诺塔问题,问是否存在一种符合规则的初始摆放方式,使得将其全部移动到其中一根柱子所用次数小于等于$2^n - 1$.

Solution 2

不存在.

证明方式类似原初问题的证明,考虑最大的那个圆盘是否到达终点.如果到达则可以去掉它,用数学归纳证明不存在;如果还未到达,同样用数学归纳得到不等式.

Example3(《具体数学》1.10)

汉诺塔问题,但是移动圆盘时只能从A移动到B,从B移动到C,从C移动到A.一开始所有圆盘都在A,求将它们全部移动到B的最小操作次数,以及将他们从B移动回A的最小操作次数.

Solution 3

令$Q_n$为将n个圆盘从A移动到B的最小操作次数,令$R_n$为将n个圆盘从B移动回A的最小操作次数.

先考虑边界情况,$Q_0 = 0 , R_0 = 0$.

我们考虑,由于柱子间在移动过程中是无区别的,因此$Q_n$的实质是将n个圆盘移动到它的下一个柱子的最小操作次数,$R_n$的实质是将n个圆盘移动到它的上一个柱子的最小操作次数.

在将最大的圆盘移动到下一根柱子前,一定要先把上面的圆盘全部移动到上一根柱子上,最后再移动回来.

显然有$Q_n = 2 R_{ n - 1 } + 1 , 1 \leq n$.

在将最大的圆盘移动到上一根柱子前,一定要先把他移动到下一根柱子上,这个步骤要求我们把其他的圆盘移动到上一根柱子上.在这之后,我们又要把所有圆盘放到上一根柱子上来让最大圆盘到目标柱子,最后再移动回来.

有$R_n = R_{ n - 1 } + 1 + Q_{ n - 1 } + 1 + R_{ n - 1 } = Q_n + Q_{ n - 1 } + 1 , 1 \leq n$.

Example4(《具体数学》1.11)

汉诺塔问题,但是每种大小的圆盘有两个,且其中一个可以摆放在另一个的上面.

a.如果相同圆盘无区别,求最小操作次数.

b.如果相同圆盘有区别,且最后需要还原原本二者的上下顺序,求最小操作次数.

Solution 4

a.仍然令$T_n$为n对圆盘的最小操作次数,显然$T_n = 2 T_{ n - 1 } + 2 , T_0 = 0$,可解得$T_n = 2^{ n + 1 } - 2$.

b.令$Q_n$为n对圆盘的最小操作次数,观察a问题,我们可以发现a问题转移之后,只有最下面的两个圆盘会交换顺序.而如果我们在b问题中只关注最下层两个圆盘的顺序,我们发现$Q_n = T_{ n - 1 } + 1 + T_{ n - 1 } + 1 + T_{ n - 1 } + 1 + T_{ n - 1 } = 4 T_{ n - 1 } + 3 = 2^{ n + 2 } - 5$.

我们进行了四次a操作,那么次下面两个圆盘自然就顺序与原本相同了,因此这里的$Q_n$就是答案.

Example5(《具体数学》1.12)

类似Problem11,但第$i$大的圆盘有$k_i$个.

Solution 5

无区别,只是$T_n = 2 T_{ n - 1 } + k_n , T_0 = 0$.

如果求封闭形式的话,显然有$T_n = \sum_{ i = 1 }^n 2^{ n - i } k_i$.

递归式的封闭形式

在上述问题中，我们已经有了以下式子：

$T_n = 2 T_{ n - 1 } + 1 , n > 0 , T_0 = 0$.

如果$n$很大，那么一步一步去计算是很复杂的，现在我们想知道一种更为快速的求出$T_n$的方法.

换句话说，我们想要把$T_n$表示为只与n有关的式子，我们称其为该递归式的封闭形式.

寻找循环节

Example(《具体数学》1.8)

解递归式:$Q_n = \begin{cases}\alpha & n = 0 \ \beta & n = 1 \ \frac{ ( 1 + Q_{ n - 1 } ) }{ Q_{ n - 2 } } & n > 1\end{cases}$,保证$\forall n , Q_n > 0$.

Solution

注意到$Q_2 = \frac{ \beta + 1 }{ \alpha } , Q_3 = \frac{ \beta + \alpha + 1 }{ \beta \alpha } , Q_4 = \frac{ 1 + \alpha }{ \beta } , Q_5 = \alpha , Q_6 = \beta$.

显然该递归式存在长度为$5$的循环节.

数学归纳法

观察T序列的前几项，可以发现似乎有$T_n = 2^n - 1$.

现在我们来证明它：

1.该公式对于$n = 0$成立，显然可验证.

2.若该公式对$n = k$时成立，那该公式必然对$n = k + 1$成立.

因为有$T_{ k + 1 } = 2 T_k + 1 = 2 \times 2^k + 2 - 1 = 2^{ k + 1 } - 1$.

以上过程被称为数学归纳法.

Example(《具体数学》1.9)

求证:$\prod_{ i = 1 }^n x_i \leq ( \frac{ \sum_{ i = 1 }^n x_i }{ n } )^n , \forall i \in N_+ , 1 \leq i \leq n , 0 \leq x_i$.

Solution

使用反向归纳法.

1.$n = 2$时,即基本不等式,显然成立.

2.若该式子对$n = k$时成立,则该式子对n=2k时也成立.

不妨令$A_1 = \sqrt[k]{ \prod_{ i = 1 }^k x_i } , B_1 = \sqrt[k]{ \prod_{ i = k + 1 }^{ 2 k } x_i } , A_2 = ( \frac{ \sum_{ i = 1 }^k x_i }{ k } ) , B_2 = ( \frac{ \sum_{ i = k + 1 }^{ 2 k } x_i }{ k } )$,显然有$A_1 \leq A_2 , B_1 \leq B_2$.

同时有$( \frac{ A_2 + B_2 }{ 2 } ) \geq \sqrt{ A_2 B_2 } \geq \sqrt{ A_1 B_1 }$.

3.若该式子对$n = k$时成立,则该式子对$n = k - 1$的时候也成立.

令$x_k = \frac{ \sum_{ i = 1 }^{ k - 1 } x_i }{ k - 1 }$,有$x_k \prod_{ i = 1 }^{ k - 1 } x_i \leq ( x_k )^k$.

则显然$n = k - 1$时也成立.

由1和2,我们知道了对于n是二的整数次幂的情况,该公式成立,由3,我们又可以知道该公式对于任意一个存在比他大的二的整数次幂的数成立,因此该公式成立.

换元

考虑令$U_n = T_n + 1$,显然有:$T_n + 1 = 2 T_{ n - 1 } + 2$.即$U_n = 2 U_{ n - 1 }$,显然$U_n = 2^n$,则$T_n = 2^n - 1$.

这个做法可以做掉所有形如$a_{ n + 1 } = pa_n + q$的递归式.我们有:

$a_{ n + 1 } + \frac{ q }{ p - 1 } = p ( a_n + \frac{ q }{ p - 1 } )$

换元做掉这个式子.

转化和式

考虑递归式$a_n T_n = b_n T_{ n - 1 } + c_n$.如果我们能找到一个不为0的求和因子$s_n$并满足$s_n b_n = s_{ n - 1 } a_{ n - 1 }$.那么我们两面同时乘以$s_n$,显然有：$s_n a_n T_n = s_{ n - 1 } a_{ n - 1 } T_{ n - 1 } + c_n s_n$.

令$S_n = s_n a_n T_n$.显然有$S_n = s_0 a_0 T_0 + \sum_{ i = 1 }^n s_i c_i$,则$T_n = \frac{ S_n }{ s_n a_n }$.

而我们也会发现$s_n = \frac{ \prod_{ i = 1 }^{ n - 1 } a_i }{ \prod_{ i = 1 }^n b_i }$.

Example1(快速排序时间复杂度)

结论:排序$n$个数时,其期望复杂度满足:

$C_n = \begin{cases} 0 & n = 0 , 1 \\ n + 1 + \frac{ 2 }{ n } \sum_{ i = 0 }^{ n - 1 } C_k & n > 1 \end{cases}$

不妨考虑两边同时乘以$n$,有 $nC_n = n^2 + n + 2 \sum_{ i = 0 }^{ n - 1 } C_i , n > 1$ .

显然也有$( n - 1 ) C_{ n - 1 } = ( n - 1 )^2 + n - 1 + 2 \sum_{ i = 0 }^{ n - 2 } C_i , n > 2$.

二式相消,有$nC_n - ( n - 1 ) C_{ n - 1 } = 2 n + 2 C_{ n - 1 } , n > 2$.

而同时有$C_2 = 3$.即:$nC_n = ( n + 1 ) C_{ n - 1 } + 2 n , n > 2$,可以使用转化和式的方法,两边乘以$\frac{ 1 }{ n ( n + 1 ) }$解决.

Example2

已知$a_1 = 1$,$a_n = \sqrt{ S_n } + \sqrt{ S_{ n - 1 } }$,求$a_n$.

注意到$a_n = S_n - S_{ n - 1 }$,则有$\sqrt{ S_n } - \sqrt{ S_{ n - 1 } } = 1$,于是$\sqrt{ S_n } = n$,$S_n = n^2$,$a_n = 2 n - 1$.

成套方法

如果我们有

\alpha & n=1\\

2f(\frac n 2)+\beta & n=2k,k\in \mathbb{N_+}\\

2f(\frac {n-1}2)+\gamma &n=2k+1,k\in \mathbb{N_+}

\end{cases}

其中$n = 2^m + l$且$2^m \leq n < 2^{ m + 1 }$.

该如何求出$f ( n )$的封闭形式呢?

由于所有的未知数都是以加法运算连接,显然有$f ( n ) = A ( n ) \alpha + B ( n ) \beta + C ( n ) \gamma$,而有$A 、 B 、 C$互不影响且$\alpha \beta \gamma$与$ABC$无关.

那无论$\beta$和$\gamma$的取值如何,$A ( n )$都不会受到影响,我们考虑$\beta = \gamma = 0$的特殊情况,此时显然有$A ( n ) = 2^m$.

接下来,我们考虑取$\alpha \beta \gamma$的特殊值,去得到ABC之间的关系.

例如，当$f ( n ) = 1$时，由递推式可知$\alpha = 1 , \beta = \gamma = - 1$,那么有$A ( n ) - B ( n ) - C ( n ) = f ( n ) = 1$.

同理，$f ( n ) = n$时，可知$\alpha = 1 , \beta = 0 , \gamma = 1$,此时有$A ( n ) + C ( n ) = f ( n ) = n$.

显然可以通过解方程求得$B ( n )$和$C ( n )$.

这个方法显然是通用方法,式子仅仅是例子,事实上,只要我们能证明$ABC$互不影响且$\alpha \beta \gamma$与$ABC$无关,我们就可以使用这个方法.

这个东西的原理是什么呢?显然是因为其中存在一个线性无关性对吧.

线性递推

一个常系数的$k$阶线性递推关系形如:

$\begin{aligned} a_n & = P_n + \sum_{ i = 1 }^k c_i a_{ n - i } , n \geq k \\ a_0 & = C_0 , a_1 = C_1 , . . . , a_{ k - 1 } = C_{ k - 1 } \end{aligned}$

当$P = 0$时,称作齐次线性递推.

特征方程

我们称方程$r^k = \sum_{ i = 1 }^k c_i r^{ k - i }$是该递推关系的特征方程,方程的解叫做该递推关系的特征根.

二阶线性齐次递推

若其特征方程有两个不同的根$r_1$和$r_2$,那么存在两个常数$\alpha_1$和$\alpha_2$,满足$a_n = \alpha_1 r_1^n + \alpha_2 r_2^n$.

若其特征方程有两个相同的根$r$,那么存在两个常数$\alpha_1$和$\alpha_2$,满足$a_n = \alpha_1 r^n + \alpha_2 nr^n$.

先考虑前者的证明,首先考虑对于$n = 0$或者$n = 1$的情况,我们考虑求出一组$\alpha_1$和$\alpha_2$来满足:

$\begin{aligned} C_0 & = \alpha_1 + \alpha_2 \\ C_1 & = \alpha_1 r_1 + \alpha_2 r_2 \end{aligned}$

若$r_1 \ne r_2$,可以解得:

$\begin{aligned} \alpha_1 & = \cfrac{ C_1 - C_0 r_2 }{ r_1 - r_2 } \\ \alpha_2 & = C_0 - \alpha_1 \end{aligned}$

接下来考虑数学归纳:

$\begin{aligned} a_n & = c_1 a_{ n - 1 } + c_2 a_{ n - 2 } \\ & = c_1 ( \alpha_1 r_1^{ n - 1 } + \alpha_2 r_2^{ n - 1 } ) + c_2 ( \alpha_1 r_1^{ n - 2 } + \alpha_2 r_2^{ n - 2 } ) \\ & = \alpha_1 ( c_1 r_1^{ n - 1 } + c_2 r_1^{ n - 2 } ) + \alpha_2 ( c_1 r_2^{ n - 1 } + c_2 r_2^{ n - 2 } ) \\ & = \alpha_1 r_1^n + \alpha_2 r_2^n \end{aligned}$

接下来考虑后者,首先我们有$\Delta = c_1^2 + 4 c_2 = 0$,考虑初始条件:

$\begin{aligned} C_0 & = \alpha_1 \\ C_1 & = \alpha_1 r + \alpha_2 r \\ \end{aligned}$

接下来我们考虑数学归纳:

$\begin{aligned} a_n & = c_1 a_{ n - 1 } + c_2 a_{ n - 2 } \\ & = c_1 ( \alpha_1 r^{ n - 1 } + \alpha_2 nr^{ n - 1 } - \alpha_2 r^{ n - 1 } ) + c_2 ( \alpha_1 r^{ n - 2 } + \alpha_2 nr^{ n - 2 } - 2 \alpha_2 r^{ n - 2 } ) \\ & = a_n - c_1 \alpha_2 r^{ n - 1 } - 2 c_2 \alpha_2 r^{ n - 2 } \end{aligned}$

我们接下来只需证明$c_1 r + 2 c_2 = 0$即可.根据方程,不难发现$r = \cfrac{ c_1 }{ 2 }$,根据$\Delta = 0$,自然得证.

更一般的情况

直接在复数域上定义$f_k ( x ) = \{ n^k x^n \}_{ n = 0 }^\infty$,此时我们规定$0^0 = 1$.特别地,当$x = 0$的时候,定义$f_k ( x )$的第$k$项是$1$,其余项是$0$.在此基础上定义线性映射$T : ( a_n )_{ n = 0 }^\infty \mapsto ( a_{ n + 1 } )_{ n = 0 }^\infty$,立刻见到:$( T - x )^{ k + 1 } f_k ( x ) = 0 , ( T - x )^k f_k ( x ) \ne 0$.原因只需简单数学归纳.而此还可以引出$f_0 ( x ) , f_1 ( x ) , \cdots$线性无关.

在此基础上观察线性递推$a_{ n + d } = c_{ d - 1 } a_{ n + d - 1 } + \cdots + c_0 a_n$,不妨取$G ( x ) = x^d - c_{ d - 1 } x^{ d - 1 } - \cdots - c_0$,立刻应当见到如果$a$是$G$的根并且重数为$e ( a )$,那么$f_{ 0 } ( x ) , \cdots , f_{ e ( a ) - 1 } ( a )$都在$\ker f ( T )$中.这恰好是该线性递推空间的维数个.我们需要说明它们线性无关,不妨反证,假设出现了形如$\sum_j w_i f_i ( y ) = \sum_j w_j f_j ( x )$的情况,此时对右边直接操作若干次$( T - x )$就可以把右边全部消成$0$,在对着左边消几次就可以使得左边只留下最高次项,这个时候发现最高次项是消不掉的,原因是将每一个位置看作关于$n$的多项式右边的$( T - x )$是不会改变左边这边的每一个位置多项式的$\deg$,这当然意味着不可能消干净.

再再进一步

我们都知道矩阵加速:也就是$\vec{ x }_{ k + 1 } = A \vec{ x }$,$\vec{ x }_{ n } = A^n \vec{ x }_0$.而我们又知道CH定理:$p ( A ) = 0$,我们用多项式取膜,有$A^n = p ( A ) F ( A ) + G ( A ) = G ( A )$,这就是解.

约瑟夫问题

考虑n个人围成一圈,从第一个人开始,每隔一个人就杀掉一个人.如10个人围成一圈时,杀人的顺序是$2 , 4 , 6 , 8 , 10 , 3 , 7 , 1 , 9$.问最后幸存下来的人编号.

首先一定有J(1)=1.考虑第一遍杀掉n号或者n-1号之后,对整个圆圈进行重新编号.

那么当人数是偶数时,我们有$J ( 2 n ) = 2 J ( n ) - 1$;当人数是奇数时,我们杀掉一号,然后有$J ( 2 n + 1 ) = 2 J ( n ) + 1$.

整理得到:

$J ( n ) = \begin{cases} 1 & n = 1 \\ 2 J ( \frac{ n }{ 2 } ) - 1 & n = 2 k , k \in \mathbb{ N_+ } \\ 2 J ( \frac{ n - 1 }{ 2 } ) + 1 & n = 2 k + 1 , k \in \mathbb{ N_+ } \end{cases}$

仍然可以使用数学归纳，如果令$n = 2^m + l 且 2^m \leq n < 2^{ m + 1 }$.

有$J ( n ) = 2 l + 1$.

要是注意力没有那么集中怎么办呢?考虑到这个东西显然和取膜有着不可分割的关系,我们不妨从$0$开始编号:

$J ( n ) = \begin{cases} 0 & n = 1 \\ 2 J ( \frac{ n }{ 2 } ) & n = 2 k , k \in \mathbb{ N_+ } \\ 2 J ( \frac{ n - 1 }{ 2 } ) + 2 & n = 2 k + 1 , k \in \mathbb{ N_+ } \end{cases}$

这下相信$J ( n )$是多少就很显然了,将$n$写成二进制的形式,这个就相当于把首位$1$抹去然后在末尾加个$0$.

Example(《具体数学》1.15)

求约瑟夫问题中最后一名被杀死的人的编号.

Solution

显然有:

$J ( n ) = \begin{cases} 2 & n = 2 \\ 1 & n = 3 \\ 2 J ( \frac{ n }{ 2 } ) - 1 & n = 2 k + 2 , k \in \mathbb{ N_+ } \\ 2 J ( \frac{ n - 1 }{ 2 } ) + 1 & n = 2 k + 3 , k \in \mathbb{ N_+ } \end{cases}$

从$0$开始编号,自然有:

$J ( n ) = \begin{cases} 1 & n = 2 \\ 0 & n = 3 \\ 2 J ( \frac{ n }{ 2 } ) & n = 2 k + 2 , k \in \mathbb{ N_+ } \\ 2 J ( \frac{ n - 1 }{ 2 } ) + 2 & n = 2 k + 3 , k \in \mathbb{ N_+ } \end{cases}$

显然$J ( n )$也可以用二进制表达其形式.

和式

和式的基本运算

分配律:

$\sum_{ i \in S } ca_i = c \sum_{ i \in S } a_i$

一般分配律:

$\sum_{ i } \sum_{ j } a_{ i } b_j = ( \sum_{ i } a_i ) ( \sum_j b_j )$

结合律:

$\sum_{ i \in S } ( a_i + b_i ) = \sum_{ i \in S } a_i + \sum_{ i \in S } b_i$

交换律:

$\sum_{ i \in S } a_i = \sum_{ p ( i ) \in S } a_{ p ( i ) }$

交换求和顺序:

$\begin{aligned} \sum_{ i } \sum_{ j } a_{ i , j } [ P ( i , j ) ] & = \sum_{ j } \sum_{ i } a_{ i , j } [ P ( i , j ) ] \\ \sum_{ i = 1 }^n \sum_{ j = i }^n a_{ i , j } & = \sum_{ j = 1 }^n \sum_{ i = 1 }^j a_{ i , j } \end{aligned}$

和式的封闭形式

交换顺序法

Example1(等差数列求和)

我们有:

$\begin{aligned} S_n & = \sum_{ i = 0 }^n ( ai + b ) = \sum_{ i = 0 }^n ( a ( n - i ) + b ) \\ 2 S_n & = \sum_{ i = 0 }^n ( an + 2 b ) = an ( n + 1 ) + 2 b ( n + 1 ) \\ S_n & = ( n + 1 ) ( \frac{ an }{ 2 } + b ) \end{aligned}$

Example2(切比雪夫单调不等式)

令$S = \sum_{ 1 \leq i < j \leq n } ( a_j - a_i ) ( b_j - b_i ) = \sum_{ 1 \leq j < i \leq n } ( a_j - a_i ) ( b_j - b_i )$.

考虑恒等式$[ 1 \leq j < i \leq n ] + [ 1 \leq i < j \leq n ] = [ 1 \leq j , i \leq n ] - [ 1 \leq i = j \leq n ]$.

那么我们有:

$\begin{aligned} 2 S & = \sum_{ 1 \leq i , j \leq n } ( a_j - a_i ) ( b_j - b_i ) - \sum_{ 1 \leq i = j \leq n } ( a_j - a_i ) ( b_j - b_i ) \\ & = \sum_{ 1 \leq i , j \leq n } ( a_j - a_i ) ( b_j - b_i ) \\ & = 2 n \sum_{ i = 1 }^n a_i b_i - 2 ( \sum_{ i = 1 }^n a_i ) ( \sum_{ j = 1 }^n b_j ) \\ ( \sum_{ i = 1 }^n a_i ) ( \sum_{ j = 1 }^n b_j ) & = n \sum_{ i = 1 }^n a_i b_i - \sum_{ 1 \leq i < j \leq n } ( a_j - a_i ) ( b_j - b_i ) \end{aligned}$

显然有以下式子:

(\sum_{i=1}^na_i)(\sum_{j=1}^nb_j)\geq n\sum_{i=1}^na_ib_i，\forall i<j，a_i\leq a_j且b_i\geq b_j\\

上式被称为切比雪夫单调不等式.

值得一提的是,切比雪夫单调不等式其实是排序不等式的一个特化版本.

Example3(拉格朗日恒等式)

证明:

$\begin{aligned} \sum_{ 1 \leq j < k \leq n } ( a_j b_k - a_k b_j )^2 & = ( \sum_{ i = 1 }^n a_i^2 ) ( \sum_{ i = 1 }^n b_i^2 ) - ( \sum_{ i = 1 }^n a_i b_i )^2 \\ \end{aligned}$

有:

$\begin{aligned} S_n & = \sum_{ 1 \leq j < k \leq n } ( a_j b_k - a_k b_j )^2 \\ 2 S_n & = \sum_{ j = 1 }^n \sum_{ k = 1 }^n ( a_j b_k - a_k b_j )^2 \\ & = \sum_{ j = 1 }^n \sum_{ k = 1 }^n ( a_j^2 b_k^2 - 2 a_j a_k b_j b_k + a_k^2 b_j^2 ) \\ & = 2 ( \sum_{ i = 1 }^n a_i^2 ) ( \sum_{ i = 1 }^n b_i^2 ) - 2 ( \sum_{ i = 1 }^n a_i b_i )^2 \end{aligned}$

扰动法

Example1(等比数列求和)

$\begin{aligned} S_n & = \sum_{ i = 0 }^n ax^i \\ & = a + \sum_{ i = 1 }^n ax^i \\ & = a + x \sum_{ i = 0 }^{ n - 1 } ax^i \\ & = a + xS_{ n - 1 } \end{aligned}$

而$S_{ n - 1 } + ax^n = S_n = a + xS_{ n - 1 }$,有$S_n + ax^{ n + 1 } = a + xS_n , S_n = a \frac{ x^{ n + 1 } - 1 }{ x - 1 }$，其中$x \ne 1$.

Example2(平方和公式)

如果直接对该公式使用扰动法:

$\begin{aligned} S_n & = \sum_{ i = 0 }^n i^2 = \sum_{ i = 0 }^{ n - 1 } i^2 + n^2 \\ & = \sum_{ i = 1 }^n ( i - 1 )^2 + n^2 \\ & = S_n - 2 \sum_{ i = 1 }^n i + n + n^2 \end{aligned}$

我们无法得到$S_n$的封闭形式,但我们发现我们得到了$\sum_{ i = 1 }^n i$的封闭形式.

那以此类推,我们设$W_n = \sum_{ i = 0 } i^3$.

$\begin{aligned} W_n & = \sum_{ i = 0 }^{ n - 1 } i^3 + n^3 \\ & = \sum_{ i = 1 }^n ( i - 1 )^3 + n^3 \\ & = \sum_{ i = 1 }^n i^3 - 3 \sum_{ i = 1 }^n i^2 + 3 \sum_{ i = 1 }^n i - n + n^3 \\ & = W_n - 3 S_n + 3 \frac{ n + n^2 }{ 2 } - n + n^3 \\ S_n & = \frac{ n + n^2 }{ 2 } - \frac{ n - n^3 }{ 3 } \\ & = \frac{ n + 3 n^2 + 2 n^3 }{ 6 } \\ & = \frac{ n ( 1 + 3 n + 2 n^2 ) }{ 6 } \\ & = \frac{ n ( 2 n + 1 ) ( n + 1 ) }{ 6 } \end{aligned}$

Example3(《具体数学》2.20)

令$H_n = \sum_{ k = 1 }^n \frac{ 1 }{ k }$,求$\sum_{ i = 0 }^n H_i$.

Solution3

不妨考虑$\sum_{ i = 0 }^n iH_{ i }$的值.

$\begin{aligned} \sum_{ i = 0 }^n iH_{ i } & = \sum_{ i = 1 }^n [ ( i - 1 + 1 ) H_{ i - 1 } + 1 ] \\ & = n + \sum_{ i = 0 }^{ n - 1 } H_i + \sum_{ i = 0 }^{ n } iH_i - nH_n \\ \sum_{ i = 0 }^{ n - 1 } H_i & = n ( H_n - 1 ) \\ \sum_{ i = 0 }^n H_i & = ( n + 1 ) ( H_{ n + 1 } - 1 ) \\ \end{aligned}$

Example4(《具体数学》2.21)

求$S_n = \sum_{ i = 0 }^n ( - 1 )^{ n - i } , T_n = \sum_{ i = 0 }^n ( - 1 )^{ n - i } i , U_n = \sum_{ i = 0 }^n ( - 1 )^{ n - i } i^2$.

Solution 4

$\begin{aligned} S_n & = \sum_{ i = 1 }^{ n } ( - 1 )^{ n - i } + ( - 1 )^n \\ - S_{ n - 1 } + 1 & = ( - 1 )^n + \sum_{ i = 0 }^{ n - 1 } ( - 1 )^{ n - 1 - i } \\ - S_{ n - 1 } + 1 & = ( - 1 )^n + S_{ n - 1 } \\ S_{ n - 1 } & = \frac{ 1 - ( - 1 )^n }{ 2 } \\ S_n & = \frac{ 1 + ( - 1 )^n }{ 2 } \end{aligned}$ $\begin{aligned} T_{ n } & = \sum_{ i = 1 }^n ( - 1 )^{ n - i } i \\ - T_{ n - 1 } + n & = \sum_{ i = 1 }^n ( - 1 )^{ n - i } ( i - 1 ) + \sum_{ i = 1 }^n ( - 1 )^{ n - i } \\ - T_{ n - 1 } + n & = \sum_{ i = 0 }^{ n - 1 } ( - 1 )^{ n - i - 1 } i + \sum_{ i = 0 }^n ( - 1 )^{ n - i } - ( - 1 )^n \\ - T_{ n - 1 } + n & = T_{ n - 1 } + S_n - ( - 1 )^n \\ n - \frac{ 1 - ( - 1 )^n }{ 2 } & = 2 T_{ n - 1 } \\ T_n & = \frac{ 1 }{ 2 } ( n + 1 + \frac{ - 1 - ( - 1 )^n }{ 2 } ) = \frac{ 1 }{ 2 } ( n + \frac{ 1 - ( - 1 )^n }{ 2 } ) \end{aligned}$ $\begin{aligned} U_n & = \sum_{ i = 1 }^n ( - 1 )^{ n - i } i^2 \\ - U_{ n - 1 } + n^2 & = \sum_{ i = 1 }^n ( - 1 )^{ n - i } ( i - 1 + 1 )^2 \\ - U_{ n - 1 } + n^2 & = \sum_{ i = 1 }^n ( - 1 )^{ n - i } ( i - 1 )^2 + 2 \sum_{ i = 1 }^n ( - 1 )^{ n - i } ( i - 1 ) + \sum_{ i = 1 }^n ( - 1 )^{ n - i } \\ - U_{ n - 1 } + n^2 & = \sum_{ i = 0 }^{ n - 1 } ( - 1 )^{ n - i - 1 } i^2 + 2 \sum_{ i = 0 }^{ n - 1 } ( - 1 )^{ n - i - 1 } i + \sum_{ i = 0 }^{ n - 1 } ( - 1 )^{ n - i - 1 } \\ - U_{ n - 1 } + n^2 & = U_{ n - 1 } + 2 T_{ n - 1 } + S_{ n - 1 } \\ 2 U_{ n - 1 } & = n^2 - 2 T_{ n - 1 } - S_{ n - 1 } \\ 2 U_{ n - 1 } & = n^2 - ( n - \frac{ 1 - ( - 1 )^n }{ 2 } ) - \frac{ 1 - ( - 1 )^n }{ 2 } \\ 2 U_{ n - 1 } & = n^2 - n \\ U_n & = \frac{ n ( n + 1 ) }{ 2 } \end{aligned}$

转化为递归式

考虑和式$S_n = \sum_{ i = 0 }^n f ( i ) = S_{ n - 1 } + f ( n ) \\$，显然是递归式形式.

因此递归式所可以使用的方法同样可以在和式中使用.

Example1(《具体数学》2.13)

求$\sum_{ i = 0 }^n ( - 1 )^i i^2 \\$.

Solution1

令$S ( n ) = \sum_{ i = 0 }^n ( - 1 )^i i^2 = S ( n - 1 ) + ( - 1 )^n n^2$,考虑使用成套方法.

不妨令$S ( n ) = S ( n - 1 ) + ( - 1 )^n ( \alpha + \beta n + \gamma n^2 ) = \alpha A ( n ) + \beta B ( n ) + \gamma C ( n )$.

令$S ( n ) = ( - 1 )^n n , 可以解得 \alpha = - 1 , \beta = 2 , \gamma = 0$,有$( - 1 )^n n = - A ( n ) + 2 B ( n )$.

令$S ( n ) = ( - 1 )^n n^2 , 可以解得 \alpha = 1 , \beta = - 2 , \gamma = 2$,有$( - 1 )^n n^2 = A ( n ) - 2 B ( n ) + 2 C ( n )$.

显然可解得$2 C ( n ) = ( - 1 )^n n^2 + ( - 1 )^n n , C ( n ) = ( - 1 )^n \frac{ n ( n + 1 ) }{ 2 }$.

而原式中,$S ( n ) = C ( n ) = ( - 1 )^n \frac{ n ( n + 1 ) }{ 2 }$.

Example2(《具体数学》2.19)

有$2 T_n = nT_{ n - 1 } + 3 n ! , T_0 = 5$,求$T_n$.

Solution 2

令$s_n = \frac{ 2^{ n - 1 } }{ n ! }$,两边同时乘以$s_n$,有$\frac{ 2^n }{ n ! } T_n = \frac{ 2^{ n - 1 } }{ ( n - 1 ) ! } T_{ n - 1 } + 3 \times 2^{ n - 1 } \\$.

令$S_n = \frac{ 2^n }{ n ! } T_n$,有:

$\begin{aligned} S_n & = S_{ n - 1 } + 3 \times 2^{ n - 1 } \\ & = 5 + 3 \sum_{ i = 0 }^{ n - 1 } 2^i \\ & = 5 + 3 \times 2^{ n + 1 } - 3 \\ & = 3 \times 2^{ n } + 2 \\ T_n & = 3 n ! + \frac{ n ! }{ 2^{ n - 1 } } \end{aligned}$

转化为积分形式

Example1(平方和公式)

考虑先求出一个近似解,然后再求误差.

考虑函数$f ( x ) = x^2$,显然$\int_0^n x^2 dx = \frac{ n^3 }{ 3 } \sim S_n \\$.

接下来,我们考虑求得二者之间的误差,设$E_n = S_n - \frac{ n^3 }{ 3 } \\$,对其使用扰动法:

$\begin{aligned} E_n & = S_n - \frac{ n^3 }{ 3 } \\ & = S_{ n - 1 } + n^2 - \frac{ ( n - 1 + 1 )^3 }{ 3 } \\ & = S_{ n - 1 } + n^2 - \frac{ ( n - 1 )^3 }{ 3 } - ( n - 1 )^2 - ( n - 1 ) - \frac{ 1 }{ 3 } \\ & = E_{ n - 1 } + n^2 - n^2 + 2 n - 1 - n + 1 - \frac{ 1 }{ 3 } \\ & = E_{ n - 1 } + n - \frac{ 1 }{ 3 } \end{aligned}$

这样就得到了递归式,可以求得封闭形式.

还有一种方法是:

$\begin{aligned} E_n & = S_n - \int_0^n x^2 dx \\ & = \sum_{ k = 1 }^n ( k^2 - \int_{ k - 1 }^k x^2 dx ) \\ & = \sum_{ k = 1 }^n ( k^2 - \frac{ k^3 - ( k - 1 )^3 }{ 3 } ) \\ & = \sum_{ k = 1 }^n ( k - \frac{ 1 }{ 3 } ) \end{aligned}$

这是一个简单的和式.而$S_n = E_n + \frac{ n^3 }{ 3 } \\$,显然也可以求得.

Example2(某浙江高考题)

已知$a_1 = 1 , a_{ n + 1 } - a_n = - \frac{ 1 }{ 3 } a_n^2$,估计$a_n$的值.

考虑构造一个函数$f ( n )$使得$f ( n ) \approx a_n$,那我们就可以将$a_{ n + 1 } - a_n \approx f_n$.

这个第一眼看上去就很有道理,而事实上也确实很有道理,原因是根据拉格朗日中值定理,$\exists x_0 \in [ n , n + 1 ] , f ‘ ( x_0 ) = f ( n + 1 ) - f ( n )$,而对于增长率变化不大的函数,直接认为$f ‘ ( x_0 ) = f ‘ ( n )$是有理可循的!

然后,原式子就变成了一个微分方程了,带入$f ( 1 ) = 1$解得$f ( n ) = \frac{ 3 }{ n + 2 }$.这个精度已经足够选出来原本的放缩题的答案了.

令$a_n = \frac{ 3 }{ n + 2 } - b_n$,带入化简,得到$\{ b_n \}$的递推式:

$\begin{aligned} \frac{ 3 }{ n + 3 } - b_{ n + 1 } & = ( \frac{ 3 }{ n + 2 } - b_n ) ( 1 - \frac{ 1 }{ n + 2 } + \frac{ b_n }{ 3 } ) \\ b_{ n + 1 } - \frac{ 3 }{ n + 3 } & = ( b_n - \frac{ 3 }{ n + 2 } ) ( \frac{ n + 1 }{ n + 2 } + \frac{ b_n }{ 3 } ) \\ b_1 & = 0 , b_{ n + 1 } = \frac{ b_n^2 }{ 3 } + \frac{ n }{ n + 2 } b_n + \frac{ 3 }{ ( n + 2 )^2 ( n + 3 ) } \end{aligned}$

算到这里,我们可以很轻易使用数学归纳法算出$b_n \leq \frac{ 1 }{ 4 n }$,这个精度已经挺不错的了,但是也让人觉得很不满意,因为这个误差项怎么和估计项是同阶的啊.

然后我开始估计了一下这个$b_n$的阶,因为我其实没学过什么高超的高数技巧,所以我使用了OI的一些技巧来估计,不妨假设$b_n^2 < < b_n$:

那么这个$b_n$是$O ( \frac{ \ln n }{ n^2 } )$级别的.

如何理解这个级别?考虑别乱动$b_n$的系数,我们有:

$\begin{aligned} b_{ n + 1 } & = \frac{ n }{ n + 2 } b_n + \frac{ 1 }{ n ( n + 1 ) ( n + 2 ) } \\ ( n + 1 ) ( n + 2 ) b_{ n + 1 } & = n ( n + 1 ) b_n + \frac{ 1 }{ n } \\ g ( n ) & = n ( n + 1 ) b_n , g ' ( n ) = \frac{ 1 }{ n } , g ( n ) = \ln n \\ b_n & = \frac{ \ln n }{ n^2 } \end{aligned}$

这警戒我们以后乱估计的时候千万别把$O ( n^{ \epsilon } )$和$O ( 1 )$搞混了,警钟长鸣.

这个时候大概估计一下会发现$b_n \leq \frac{ 3 \ln n }{ n ( n + 1 ) }$.

展开和收缩

Example1(平方和公式)

我们有:

$\begin{aligned} S_n & = \sum_{ k = 1 }^n k^2 \\ & = \sum_{ k = 1 }^n \sum_{ i = 1 }^k k \\ & = \sum_{ i = 1 }^n \sum_{ k = i }^n k \\ & = \sum_{ i = 1 }^n \frac{ 1 }{ 2 } ( i + n ) ( n - i + 1 ) \\ & = \sum_{ i = 1 }^n \frac{ 1 }{ 2 } ( in - i^2 + i + n^2 - ni + n ) \\ & = \frac{ 1 }{ 2 } ( \sum_{ i = 1 }^n i - \sum_{ i = 1 }^n i^2 + n^3 + n^2 ) \\ & = \frac{ 1 }{ 4 } n ( n + 1 ) - \frac{ 1 }{ 2 } S_n + \frac{ n^3 + n^2 }{ 2 } \end{aligned}$

整理得到$S_n$.

Example2(《具体数学》2.14)

求$\sum_{ i = 1 }^n i 2^i \\$.

Solution 2

$\begin{aligned} \sum_{ i = 1 }^n i 2^i & = \sum_{ i = 1 }^n \sum_{ j = 1 }^i 2^i \\ & = \sum_{ j = 1 }^n \sum_{ i = j }^n 2^i \\ & = \sum_{ j = 1 }^n ( 2^{ n + 1 } - 2^j ) \\ & = n 2^{ n + 1 } - ( 2^{ n + 1 } - 2 ) \\ & = ( n - 1 ) 2^{ n + 1 } + 2 \end{aligned}$

Example3(《具体数学》2.15)

求$\sum_{ i = 1 }^n i^3 \\$.

Solution 3

$\begin{aligned} S ( n ) & = \sum_{ i = 1 }^n i^3 \\ & = \sum_{ i = 1 }^n \sum_{ j = 1 }^i i^2 \\ & = \sum_{ j = 1 }^n \sum_{ i = j }^n i^2 \\ & = \sum_{ j = 1 }^n ( \frac{ n ( n + 1 ) ( 2 n + 1 ) }{ 6 } - \frac{ ( j - 1 ) j ( 2 j - 1 ) }{ 6 } ) \\ & = \frac{ n^2 ( n + 1 ) ( 2 n + 1 ) }{ 6 } - \frac{ 1 }{ 3 } S ( n ) + \frac{ n ( n + 1 ) ( 2 n + 1 ) }{ 12 } - \frac{ n ( n + 1 ) }{ 12 } \\ S ( n ) & = \frac{ n^2 ( n + 1 )^2 }{ 4 } \end{aligned}$

ExampleEX

求$\sum_{ i = 1 }^n iq^i ( q \ne 1 )$.

SolutionEX

$\begin{aligned} \sum_{ i = 1 }^n iq^i & = \sum_{ j = 1 }^n \sum_{ i = j }^n q^i \\ & = \sum_{ j = 1 }^n \frac{ q^j - q^{ n + 1 } }{ 1 - q } \\ & = \frac{ 1 }{ q - 1 } \sum_{ j = 1 }^n ( q^{ n + 1 } - q^j ) \\ & = \frac{ 1 }{ q - 1 } ( nq^{ n + 1 } - \frac{ q^{ n + 1 } - q }{ q - 1 } ) \\ \end{aligned}$

ExampleEX2

求$\sum_{ i = 1 }^n ( ai + b ) q^{ i - 1 } ( q \ne 1 )$.

SolutionEX2

令$A = \frac{ a }{ q - 1 } , B = \frac{ b - A }{ q - 1 }$,答案为$( An + B ) q^n - B$.

有限微积分

移位算子

定义移位算子$E$，使得$Ef ( x ) = f ( x + 1 )$.

差分算子

定义差分算子$\Delta f ( x ) = f ( x + 1 ) - f ( x )$，类似于无限微积分中的D算子.

另外,不难发现有$\Delta = E - 1$.

逆差分算子

定义逆差分算子$\Sigma$,可以得到有限微积分的基本定理:

$\begin{aligned} g ( x ) & = \Delta f ( x ) \Leftrightarrow \sum g ( x ) \delta x = f ( x ) + C \\ \end{aligned}$

这里的$\Sigma$又被称为不定和式,是差分等于$g$的一个函数类.

值得一提的是,这里的$C$与无限微积分中的$C$有一定区别,这里的$C$可以是满足$p ( x ) = p ( x + 1 )$的任意一个函数而不非得是常数函数.

定和式

如果$g ( x ) = \Delta f ( x )$,那么有$\sum \nolimits_{ a }^b g ( x ) \delta x = f ( x ) |^{ b }_a = f ( b ) - f ( a ) \\$.

值得一提的是,如果$a \leq b$,显然有$\sum \nolimits_{ a }^b g ( x ) \delta x = \sum_{ x = a }^{ b - 1 } g ( x ) \\$.

但如果$a > b$,那么$\sum \nolimits_{ a }^b g ( x ) \delta x = - \sum \nolimits_b^a g ( x ) \delta x \\$.

事实上,我们一定有:$\sum \nolimits_a^b g ( x ) \delta x + \sum \nolimits_b^c g ( x ) \delta x = \sum \nolimits_a^c g ( x ) \delta x \\$.

一些基本的公式

类比无限微积分中的$D ( x^m ) = mx^{ m - 1 }$，有:

$\begin{aligned} \Delta ( x^{ \underline{ m } } ) & = mx^{ \underline{ m - 1 } } \\ \sum mx^{ \underline{ m - 1 } } \delta x & = x^{ \underline{ m } } + C , m \ne 0 \\ \\ \end{aligned}$

类比无限微积分中的$D ( \ln x ) = \frac{ 1 }{ x }$,有:

$\begin{aligned} \Delta ( H ( x ) ) & = x^{ \underline{ - 1 } } = \frac{ 1 }{ x + 1 } \\ \sum x^{ \underline{ - 1 } } \delta x & = H ( x ) + C \\ \\ \end{aligned}$

类比无限微积分中的$D ( e^x ) = e^x$,有:

$\begin{aligned} \Delta ( 2^x ) & = 2^x , \sum 2^x \delta x = 2^x + C \\ \Delta ( c^x ) & = ( c - 1 ) c^x , \sum c^x \delta x = \frac{ c^x }{ c - 1 } + C , c \ne 1 \\ \Delta ( c^{ \underline{ x } } ) & = \frac{ c^{ \underline{ x + 2 } } }{ c - x } , \sum \frac{ c^{ \underline{ x + 2 } } }{ c - x } \delta x = c^{ \underline{ x } } + C , c - x \ne 0 \\ \end{aligned}$

根据组合数公式,有:

$\begin{aligned} \Delta ( \binom{ x }{ k } ) & = \binom{ x }{ k - 1 } \\ \sum \binom{ x }{ k - 1 } \delta x & = \binom{ x }{ k } + C \end{aligned}$

Example(平方和公式)

我们有:$k^2 = k^{ \underline{ 2 } } + k^{ \underline{ 1 } } \\$.

那么:

$\begin{aligned} S_{ n - 1 } & = \sum_{ i = 0 }^{ n - 1 } i^2 \\ & = \sum_{ i = 0 }^{ n - 1 } ( i^{ \underline{ 2 } } + i^{ \underline{ 1 } } ) \\ & = \sum \nolimits_{ 0 }^n x^{ \underline{ 2 } } \delta x + \sum \nolimits_{ 0 }^n x^{ \underline{ 1 } } \delta x \\ & = \frac{ n^\underline{ 3 } }{ 3 } + \frac{ n^{ \underline{ 2 } } }{ 2 } \end{aligned}$

整理即可得到封闭形式.

值得一提的是:

与前面的方法不同，这里没有使用三次的二项式公式，而是使用了二次的斯特林公式负责将一般幂转化为下降幂.

高阶差分

考虑一阶差分是$\Delta f ( x ) = f ( x + 1 ) - f ( x )$,那么二阶差分就是$\Delta^2 f ( x ) = f ( x + 2 ) - 2 f ( x + 1 ) + f ( x )$.

类似地,我们可以通过归纳法证明$\Delta^n f ( x ) = \sum_{ k } \binom{ n }{ k } ( - 1 )^{ n - k } f ( x + k ) \\$.

事实上有一种更简单的证明方法,由于$\Delta = E - 1$,于是$\Delta^n = ( E - 1 )^n = \sum_{ k } \binom{ n }{ k } ( - 1 )^{ n - k } E^k \\$,由于$E^k f ( x ) = f ( x + k )$,即可证明原式.

另外,不难发现如果$f ( x )$是一个关于$x$的$d$次多项式,那么$\Delta f ( x )$是一个$d - 1$次多项式.同理,$\Delta^d f ( x )$会是一个常数而$\Delta^{ d + 1 } f ( x )$会是$0$,这个发现引出了牛顿级数.

Example([yLOI2020]灼)

首先不难发现对于一个位置,有意义的只有相邻的两个虫洞,设这两个位置分别为$x_1 , x_2$.

不难写出期望转移式子:$f_i = \cfrac{ 1 }{ 2 } ( f_{ i - 1 } + f_{ i + 1 } ) + 1$,并且$f_{ x_1 } = f_{ x_2 } = 0$.

接下来如何做呢?

我们先对第一个式子进行变形:

$\begin{aligned} f_i & = \cfrac{ 1 }{ 2 } ( f_{ i - 1 } + f_{ i + 1 } ) + 1 \\ 2 f_i & = f_{ i - 1 } + f_{ i + 1 } + 2 \\ f_i - f_{ i - 1 } & = f_{ i + 1 } - f_i + 2 \\ \Delta f_{ i - 1 } & = \Delta f_{ i } + 2 \\ \Delta f_i - \Delta f_{ i - 1 } & = - 2 \\ \Delta^2 f_{ i - 1 } & = - 2 \end{aligned}$

$f$的二阶差分是常数,也就是说$f$是二次多项式,不难求得其二次项系数为$- 1$又知道两个零点,显然可以得到$f$的表达式.

牛顿级数

令$f ( x ) = \sum_{ 0 \leq i \leq d } a_i x^i \\$.而由于有斯特林数可以进行幂和下降幂的转换,则我们可以将其改写为$f ( x ) = \sum_{ 0 \leq i \leq d } b_i x^{ \underline{ i } } \\$.

我们设$c_i = i ! b_i$,于是有:$f ( x ) = \sum_{ 0 \leq i \leq d } c_i \binom{ x }{ i } \\$.

也就是说,任何多项式都可以表示为二项式系数的倍数之和,我们称这样的展开式为$f ( x )$的牛顿级数.

于是不难发现有:$\Delta^n f ( x ) = \sum_{ 0 \leq i \leq d } c_i \binom{ x }{ i - n } \\$.如果我们令$x = 0$,则有:$\Delta^n f ( 0 ) = \begin{cases}c_n & n \leq d \ 0 & n > d\end{cases}$.那么牛顿级数的另一种表示即:$f ( x ) = \sum_{ 0 \leq i \leq d } \Delta^i f ( 0 ) \binom{ x }{ d } \\$.

另外,如果我们展开一下$c_n = \Delta^n f ( 0 )$,我们可以得到公式:

$\sum_{ k } \binom{ n }{ k } ( - 1 )^k ( \sum_{ 0 \leq i \leq n } c_i \binom{ k }{ i } ) = ( - 1 )^n c_n , n \in \mathbb{ N } \\$.

如果我们将多项式还原,由于$a_n = b_n$,有:

$\sum_{ k } \binom{ n }{ k } ( - 1 )^k ( \sum_{ 0 \leq i \leq n } a_i k^i ) = ( - 1 )^n n ! a_n , n \in \mathbb{ N } \\$.

另外,如果$x \in \mathbb{ N }$,那么我们有:$f ( x ) = \sum_{ 0 \leq k } \Delta^k f ( 0 ) \binom{ x }{ 0 }$,根据多项式推理法,这个公式对$\forall x \in \mathbb{ Z }$都成立.

于是我们可以类似泰勒级数写出无限牛顿级数:

$g ( a + x ) = \sum_{ 0 \leq k } \cfrac{ \Delta^k g ( a ) }{ k ! } x^{ \underline{ k } }$

Example

求$\sum_{ k } \binom{ n }{ k } \binom{ r - sk }{ n } ( - 1 )^k , n \in \mathbb{ N } \\$.

如果我们令$f ( k ) = \binom{ r - sk }{ n } = \sum_{ 0 \leq i \leq n } a_i k^i \\$,不难发现$a_n = \cfrac{ ( - 1 )^n s^n }{ n ! }$,于是显然原式$= s^n$.

分部求和法则(Abel求和法)

$\begin{aligned} \Delta ( uv ) & = u ( x + 1 ) v ( x + 1 ) - u ( x ) v ( x ) \\ & = u ( x + 1 ) v ( x + 1 ) - u ( x ) v ( x + 1 ) + u ( x ) v ( x + 1 ) - u ( x ) v ( x ) \\ & = v ( x + 1 ) \Delta u + u ( x ) \Delta v = Ev \Delta u + u \Delta v \\ \end{aligned}$

两边取不定和，即可得到分部求和法则:

$\sum u \Delta v = uv - \sum Ev \Delta u \\$.

分部求和用一般和式表达如下,下式又被称为Abel求和法:

$\begin{aligned} \sum_{ i = l }^{ r - 1 } ( a_{ i + 1 } - a_i ) b_i & = a_r b_r - a_l b_l - \sum_{ i = l }^{ r - 1 } a_{ i + 1 } ( b_{ i + 1 } - b_i ) \\ \sum_{ i = l }^{ r - 1 } ( \Delta a_i ) b_i & = a_r b_r - a_l b_l - \sum_{ i = l }^{ r - 1 } a_{ i + 1 } ( \Delta b_i ) \end{aligned}$

对于$l = 0 , r = n , a_0 = b_0 = 0$的特殊情况,应当有:

$\begin{aligned} \sum_{ i = 0 }^{ n - 1 } ( \Delta a_i ) b_i & = a_n b_n - \sum_{ i = 0 }^{ n - 1 } a_{ i + 1 } ( \Delta b_i ) \\ \sum_{ i = 1 }^n a_i ( b_{ i + 1 } - b_i ) & = a_n b_n - \sum_{ i = 0 }^{ n - 1 } ( \Delta a_i ) b_i \end{aligned}$

取两组数列$\alpha , \beta$,并令$\sum_{ i = 1 }^n \beta_i = B_i$,立刻有:

$\sum_{ i = 1 }^n \alpha_i \beta_i = \alpha_n B_n - \sum_{ i = 1 }^{ n - 1 } ( \alpha_{ i + 1 } - \alpha_i ) B_i$

Example1

求$\sum_{ k = 0 }^n k 2^k \\$.

根据分部求和法则，我们有:

$\sum x 2^x \delta x = x 2^x - \sum 2^{ x + 1 } \delta x = x 2^x - 2^{ x + 1 } + C \\$.

改为定和式形式，显然有:

$\sum_{ k = 0 }^n k 2^k = \sum \nolimits_0^{ n + 1 } x 2^x \delta x = ( n + 1 ) 2^{ n + 1 } - 2^{ n + 2 } + 2 = ( n - 1 ) 2^{ n + 1 } + 2 \\$.

Example2

求$\sum_{ k = 0 }^{ n - 1 } kH_k \\$.

令$u ( x ) = H_x , v ( x ) = \frac{ 1 }{ 2 } x^{ \underline{ 2 } } \\$.

带入分部求和法则，显然有:

$\sum xH_x \delta x = \frac{ x^\underline{ 2 } }{ 2 } H_x - \frac{ x^\underline{ 2 } }{ 4 } + C \\$.

带入即可求出原式$= \frac{ n^\underline{ 2 } }{ 2 } ( H_n - \frac{ 1 }{ 2 } ) \\$.

Example3(《具体数学》2.23)

求$\sum_{ i = 1 }^n \frac{ 2 i + 1 }{ i ( i + 1 ) } \\$.

Solution 3

令$u = ( 2 n + 1 ) , v = - \frac{ 1 }{ i }$,则$\Delta u = 2 , \Delta v = \frac{ 1 }{ i ( i + 1 ) }$.

根据分部求和法则,有:

$\begin{aligned} \sum_{ i = 1 }^n \frac{ 2 i + 1 }{ i ( i + 1 ) } & = ( 2 n + 3 ) \times ( - \frac{ 1 }{ n + 1 } ) + 3 - \sum_{ i = 1 }^n ( - \frac{ 2 }{ i + 1 } ) \\ & = - \frac{ 2 n + 3 }{ n + 1 } + 2 H_n + \frac{ n + 3 }{ n + 1 } = 2 H_n - \frac{ n }{ n + 1 } \end{aligned}$

Problem 4(《具体数学》2.24)

求$\sum_{ i = 0 }^{ n - 1 } \frac{ H_k }{ ( k + 1 ) ( k + 2 ) } \\$.

Solution 4

令$u = H_n , v = - \frac{ 1 }{ n + 1 } , \Delta u = \frac{ 1 }{ n + 1 } , \Delta v = \frac{ 1 }{ ( n + 1 ) ( n + 2 ) } \\$.

根据分部求和法则,有:

$\begin{aligned} \sum_{ i = 0 }^{ n - 1 } \frac{ H_k }{ ( k + 1 ) ( k + 2 ) } & = - \frac{ H_n }{ n + 1 } - \sum_{ i = 0 }^{ n - 1 } ( - \frac{ 1 }{ ( i + 2 ) ( i + 1 ) } ) \\ & = - \frac{ H_n }{ n + 1 } + \sum_{ i = 0 }^{ n - 1 } ( \frac{ 1 }{ i + 1 } - \frac{ 1 }{ i + 2 } ) \\ & = - \frac{ H_n }{ n + 1 } + H_n - ( H_n - 1 + \frac{ 1 }{ n + 1 } ) \\ & = 1 - \frac{ H_n + 1 }{ n + 1 } \end{aligned}$

贪心与构造

发表于 2025-06-23 分类于 OI Waline：

贪心

排除不优策略

Example1(CF1612E)

先把期望写开,我们发现如果选择了$t$个消息$a_1 , a_2 , . . . , a_t$,那么答案就是$\sum [ \exists j , m_i = a_j ] \cfrac{ \min ( t , k_i ) }{ t }$.显然如果$t$固定,那么每个$a_j$的贡献是独立的.于是只需要枚举$t$然后取贡献最大的.

但是,如果$t > \max \{ k_i \}$,这个时候$t - 1$的答案是$t - 1$个数之和除以$t - 1$,$t$的答案是这$t - 1$个数之和加上另一个更小的数除以$t$,而前者肯定比后者大,于是不用再进一步枚举.

于是复杂度$O ( n \max \{ k_i \} )$.

Example2(CF1592F1)

首先,二操作和三操作一定没有用,因为它们都可以用两次一操作代替.

再注意到四操作是可能有用的,因为我们拿一操作模拟四操作需要四金币的代价,而用一个四操作只需要三个金币.但是,由于拿一操作模拟四操作的时候,需要全局做一遍一操作,所以如果有两个四操作,模拟的时候两遍全局操作就可以抵消.因此,我们模拟两次四操作只需要六个金币的代价.换句话说,我们如果要用到四操作,只会使用一次或零次.

首先区间异或可以差分($b_{ i , j } = a_{ i , j } \oplus a_{ i + 1 , j } \oplus a_{ i , j + 1 } \oplus a_{ i + 1 , j + 1 }$)后转化为四个点的异或操作,而由于一操作操作了左上角的矩阵,所以它实际上是对三个在原矩阵外的点和一个在矩阵内的点操作.我们注意到如果矩阵内已经全都是$0$了,那么矩阵外不可能是$1$,也就是原矩阵也全都是$0$了.

枚举一下最后的操作是啥即可,另外注意到这一步操作必须把四个点全部变成$0$才有用,不然还需要拿一操作去补,就不如直接用一操作.

Example3(CF1592F2)

首先注意到,如果我们对$( x , y )$使用操作四,那我们不可能再对一个$( x , i )$使用操作四,不然我们就可以用四次操作一代替这两次操作四.

再通过上面的分析,注意到只有$b_{ x , y } , b_{ n , y } , b_{ x , m }$都是$1$的时候才会使用四操作,不然,如果我们使用四操作,必然会再需要一个一操作来补,这样就是至少三个金币的代价.而由于这四个点中最多只有三个$1$,所以一定不如直接用一操作来的划算.不然,如果三个都是$1$,那么用了就一定不亏,因为无论如何也需要三次一操作,而就算我们用完后$b_{ n , m }$变成$1$了,再不行也可以使用一次$1$操作来补全.

因此我们现在想要选尽可能多的三操作,满足两两操作不在同一行或同一列,这显然是一个二分图匹配问题.换句话说,如果$b_{ x , y } , b_{ n , y } , b_{ x , m }$都是$1$,我们就把$x$到$y$连一条边,然后做二分图匹配,显然是最优的.

Example4(CF1666E)

先想一下别的东西怎么求.

如果我们要求最大值最小或者最小值最大怎么办?我们可以二分后贪心,而显然它们的差就是一个答案的下界,问题在于这个下界是否可以取到.

我们冷静一下,发现在可能的方案中,第$i$条线段的右端点的位置一定是一段连续的区间.

设$f_i$表示第$i$个分界点可能的最小值,$g_i$表示第$i$个分界点可能的最大值.假设我们目前二分的最大值要小于等于$mx$,最小值要大于等于$mn$,那么我们有转移:

$\begin{aligned} f_{ i + 1 } & = \max \{ a_{ i + 1 } , f_i + mn \} \\ g_{ i + 1 } & = \min \{ a_{ i + 2 } , g_i + mx \} \\ \end{aligned}$

注意到$f$与$g$的转移是无关的,而显然对于第$i$个分界点,它可以取$[ f_i , g_i ]$中一个数,一定存在一个取法使得答案能取到下界.

为啥呢?只需让$ans_{ i }$表示第$i$条分界线是啥,那么我们$ans_i$是可以取$[ ans_{ i + 1 } - mx , ans_{ i + 1 } - mn ]$中的任何一个数字的,我们将其和上面求出的$[ f_i , g_i ]$求一下交集.如果交集为空,说明要么$ans_{ i + 1 } - mn < f_i , f_{ i + 1 } < ans_{ i + 1 } < f_i + mn$,这是不可能的.另一种情况同理不可能,这就保证了一定可以取到答案.一定能使极差$\leq mx - mn$.

Example5(2022zrtg十连测day7 Palindrome)

首先注意到同种字符的相对顺序不可能改变.于是最后的回文串是哪个字符对应哪个字符就可以确定.

这样我们的问题转化为现在有若干个点对$( l , r )$,我们想给每一个点对赋值:$a_l = i , a_r = n - i + 1$(注意如果$n$是奇数,那么中心点应该是$a_{ mid } = \frac{ n + 1 }{ 2 }$),然后使整个序列逆序对数尽可能小.

接下来讨论一下两个点对$( l_1 , r_1 )$,$( l_2 , r_2 )$之间的三种可能的关系:不交,包含,相交且不包含.会发现若$l$小则让$a_l$尽可能小就是最优的.

Example6(23省选10连测 day9 C)

强强题.

首先发现这个$\pm 1$操作很奇怪.我们不妨这么考虑:设最后的答案序列为$b$,那么答案其实就是$\sum | b_i - a_i |$.这实际上是什么呢?实际上是数轴上$a_i$和$b_i$之间的距离.既然这样,那么我们同时反转$a$和$b$,这等价于翻转数轴,答案应该是不变的.这说明什么呢?如果我挑一个$a$,将它和$x$同时反转,那么答案不变.这么做后我们可以直接清空所有$a$的最高位,只剩下$x$可能有最高位.

那$x$的最高位一定会让若干$a$往上变成它.注意到最多只会有一个$a$会向上满足$x$的最高位.证明的话同样考虑取反,如果有两个$a$满足$a_i \oplus b_i$和$a_j \oplus b_j$这一位是$1$,我们仍然考虑数轴,有$| not ( b_i ) - a_i | \leq | a_i - b_i |$,这由$a_i \oplus b_i$最高位是$1$导出.因此两个都取反一定不劣.

再考虑,我们会让哪个$a$上去满足呢?自然的想法是取代价最小的那个,因为就算它不是,这里自然地有一个待悔贪心:其它的$a$可以再变成它.

于是就做完了.

Example7(异或粽子)

Example8()

带悔贪心

Example1

给定一个数组,给出若干次操作$[ l , r , k ]$表示可以将$a [ l \cdots r ]$减一进行至多$k$次,要求操作过程中数组时刻非负,求最大能做出的操作次数.

这题的做法是,我们每次遇到一个左端点,就将所有以它为左端点的区间全部操作,并把这些区间按照右端点为关键字扔进堆里.每次遇到一个地方的值变成了负的,就从堆中找右端点最大的区间杀掉.容易发现这样是正确的.

为啥能想到带悔贪心呢?主要是因为我们发现不同的区间会彼此影响,而且有一个限制性的长期条件.因此先不管这个条件,最后再通过调整堆将这个条件调整至合法.

Example2

给定一个序列,每次可以选择相邻的两个数,使其中一个$- 1$,另一个$- 2$,求使得整个序列都小于等于$0$的最小操作次数.

我们明确一下带悔贪心的基本条件:

首先,贪心是需要保证局部最优性的,并且需要保证不考虑全局的前提下,求局部最优解就是全局最优解的一部分.按我的理解,贪心是和dp一样需要有无后效性的,你前面的决策做了就是做了,带悔贪心只能改变后面的决策的形态,而不能改变前面的决策.
不同的操作之间会彼此影响,并且我们在不看全局的状态的前提下,无法第一时间确定当前对后面最优影响的操作是啥.通常情况下,感觉带悔贪心的每个操作会影响的操作是有限的.
感觉能做带悔贪心的好像很多都可以设计一个复杂度更高的dp.不过这个似乎很合理,因为(2)告诉我们它能影响的操作大概率是不多的.

我们看这个题,第一点基本随便编个贪心都可以满足:就是先不断做$( - 2 , - 1 )$,最后不够了再加个$( - 1 , - 2 )$补一下.而第二点呢?显然每个地方的操作只会影响前后两个位置接下来的操作(当然,被影响到的位置有可能继续影响别人).

那么为什么能想到带悔贪心呢?其实只要发现有的时候$( - 1 , - 2 ) + ( - 1 , - 2 )$比$( - 2 , - 1 )$更优秀就自然能引到带悔贪心了.

好,现在我们仍然是做那个看上去就不太对的贪心:先不断做$( - 2 , - 1 )$,最后不够了再加个$( - 1 , - 2 )$补一下.我们通过样例以及其它栗子发现:有的时候$( - 1 , - 2 ) + ( - 1 , - 2 )$比$( - 2 , - 1 )$更优秀,这启发我们:能不能在做后面位置的时候将前面的$( - 2 , - 1 )$变成$( - 1 , - 2 ) + ( - 1 , - 2 )$呢?注意这里我们不能直接换:带悔贪心要求我们不能改变前面操作的状态.因此我们引入一个操作:如果当前前面存在一个$( - 2 , - 1 )$操作,那么我可以在这个位置进行一个$( 0 , - 3 )$操作.显然$( 0 , - 3 ) + ( - 2 , - 1 ) = ( - 1 , - 2 ) + ( - 1 , - 2 )$.我们完成了反悔的操作!

但是,我们直接认为$( - 1 , - 2 )$不可能反悔的原因是:它是一个补位操作,一个位置只有可能进行一次,这玩意不可能能反悔.可现在不一样了,我们的操作序列中有了两个$( - 1 , - 2 ) + ( - 1 , - 2 )$,怎么办呢?你当然可以对着这个操作再观察怎么反悔,但事实上有更高效的思路:我们直接考虑$( - 3 , 0 )$怎么反悔.这个看上去很疑惑:我们为了使$( - 2 , - 1 )$变成$( - 1 , - 2 ) + ( - 1 , - 2 )$而引入了一个新操作,这个新操作在原序列中是不存在的:它甚至有个很奇怪的限制条件:必须在前面存在$( - 2 , - 1 )$的时候才可以发动.那为什么我们可以直接考虑它如何反悔呢?

先看第一个问题:$( - 3 , 0 )$这个技能的发动是有前提条件的:前面必须有$( - 2 , - 1 )$才可以.但你注意我们是在贪心啊,我们很清楚每个地方用了几个$( - 2 , - 1 )$,也很清楚每个地方用了几个$( - 3 , 0 )$.

再看第二个问题:这个新操作为何能反悔呢?其实第一个问题解决这个问题也就解决了,由于贪心,我们知道了巨大多的信息,这个信息量是dp不能比的.因此这个条件如果dp的话看上去需要多记一维,但是贪心完全不用.

我们可以根据类似上面的操作迅速编出它怎么反悔:$( - 3 , 0 ) \rightarrow ( - 1 , - 2 ) + ( - 2 , - 1 ) = ( - 3 , 0 ) + ( 0 , - 3 )$,或者$( - 3 , 0 ) \rightarrow ( - 1 , - 2 ) + ( - 1 , - 2 ) + ( - 1 , - 2 ) = ( - 3 , 0 ) + ( 0 , - 3 ) + ( 0 , - 3 )$.

最后遇到一个点,能用$( 0 , - 3 )$就用$( 0 , - 3 )$,不够用的再补齐.这个原因也很简单:如果我们在这里不用$( - 3 , 0 )$而用其它的代替的话,你会发现无论如何都等价于$( - 3 , 0 )$然后后面再反悔.

再总结一下这个题中包含的带悔贪心:

这个带悔贪心包含若干个操作,这些操作之间可以互相转化,使得在前面进行的一个操作可以和在后面进行的一个操作一起,等价于前面进行了另一个操作.如同最经典的带悔贪心的模型,我们每次进行一个操作后,都会加入若干个可以进行的操作(在这个题中,一开始就在每个位置加入了无穷多的$( - 2 , - 1 )$和$( - 1 , - 2 )$的操作)(写一下代码就会发现,我们其实记录下了每个位置插入了多少个可行的$( - 3 , 0 )$操作).这些操作构成一个封闭的东西,使得反悔任意一个操作的反悔操作本身都可以使用若干操作表示出来.

寻找下界并证明

Example1([EER1]代价)

给你一个长度为$n$的序列$a$,保证$a_1 = a_n = 1$.每次你可以选择一个$i ( 1 < i < n )$将$a_i$删去并付出$a_{ i - 1 } a_i a_{ i + 1 }$的代价.删去$a_i$后序列两端会接起来,求删成两个$1$的最小代价.

首先注意到,如果有一个$1 < i < n$满足$a_i = 1$,那这个点最后删显然更优秀:如果我们把它删了,不仅肯定比最后删它劣(最后删它只需要$1$的代价),还有可能使原本能和它相邻的点这次和一个更大的数相邻了,显然不优秀.因此整个序列被若干个$1$所划分.接下来我们只考虑中间所有数$\geq 2$的情况.

再思考一个事实:当$a , b \geq 2$时,一定有$ab \geq a + b$.而考虑每两个相邻的点一定会被乘起来扔进答案,也就是说答案下界一定是$\sum_{ i = 2 }^{ n - 2 } a_i a_{ i + 1 } + \min_{ i = 2 }^{ n - 1 }{ a_i }$.注意到这个下界是可以构造出来的:找到每一段最小的点然后从左/右挨个删点即可.

Example2(loj3318)

首先考虑:给出一个排列,从原排列换到它的最小步数一定是它的逆序对数.因为我们可以每次找到应当被放到边界的点,然后不断把它换过去.

考虑现在构造$a$数组,每次对于还没选的最大值,显然要扔到尽可能靠后的位置,然后不断递归处理.

Example3

给定一张图,每个点上有一个权值$a_i$,我们每次可以删掉一个点以及其所有连边,代价是所有相邻的点的权值和.求删光图的最小代价.

首先注意到答案一共要更新边数次,不妨考虑边.

一条边可能对答案有两种贡献,也就是与它相邻的两个点的点权.它会对答案贡献后删的那个点的点权.显然所有边取最小值时是一个下界.这个下界是可以构造出来的:我们按照点权从大往小删即可.

Example4([UOJ280]题目难度排序)

先考虑$a_i$互不相同,那可以每次选一个最大的数,满足它加进去后整个集合的中位数$\leq$还没选的数的最小的数.注意到这里一定能构造出合法解,且如果选了另一个数一定更劣.

那如果可能存在$a_i$相同呢,我们先按照大小排序,然后选出一对小于等于所有数的中位数的$( a_i , a_{ i + 1 } )$,然后这么选:$a_i , a_{ i + 1 } , a_n , a_{ i - 1 } , a_{ n - 1 } , a_{ i - 2 } . . .$,一直到左边全部被填完,然后按照互不相同的方法填.

首先这么做一定是合法解,因为中位数会在$a_i$上震荡.其次这么做为什么是最优解呢?我们考虑一开始如果选了另一对大于中位数的相等的数,那一定不合法,因为最后会剩一些小数,会把这些东西震荡到一个更小的中位数.而如果一开始选了一个单点,接下来一定要不断选更大的点,这样比它小的数就没法加进去了.而等左边全部被填完后,由于这个时候中位数已经没有办法保持不变了,所以必定接下来要增大,而中位数不断增大只能按照互不相同的方法填.

Example5([CF1098D]Eels)

首先,我们猜测:我们一开始先让最小的两个互相吃,可能是最优秀的.接下来我们尝试证明这个猜测.

首先,对于一个不危险的操作来说,假设这次操作的两个数是$a$和$b$,其中$2 a < b$.我们尝试判断一下这个操作满足什么条件.这个时候,注意到如果$b$之前吃过别的鱼,假设是$c$和$d$(不妨假设$d \geq c$),有$b = c + d$,由鸽笼原理,发现$d > a$.这意味着:如果$a$都没被操作掉,那么$d$必不可能被操作掉,这也就是说$b$不可能出现.因此$b$在这次操作前一定没有吃过别的鱼.那互相残杀的鱼的重量就都一定小于$b$,且$a$就是所有一开始小于$b$的鱼的和.

我们按照鱼的重量从小到大排序,你会发现一次不危险操作涉及到的鱼一定是一条满足自己大于比自己小的所有鱼的重量和的两倍的鱼,我们称其为大鱼,也就是$w_i > 2 \sum_{ j = 1 }^{ i - 1 } w_j$,我们对此计数就可以完成一次操作.

那么问题又来了,这个东西一定是最小的吗?

我们考虑一个事实:我们要最小化不危险操作的数量,但很明显的一点是:每只大鱼都必须经过一次不危险操作才能变成一只更大的鱼,当然,如果它选择自杀,那么吃掉它的那只鱼会继承它的地位,在不死的情况下仍然要进行至少一次不危险操作才能变成更大的鱼,因此这显然是一个下界.而又可以构造出答案.

那么如何多组询问呢?首先发现大鱼不会很多,最多$\log w$个,我们考虑一下这个两倍的用处,我们按照值域$[ 1 , 1 ] , [ 2 , 2 ] , [ 3 , 4 ] , [ 5 , 8 ] , . . . , [ 2^{ k - 1 } + 1 , 2^k ]$将鱼分成若干组,不难发现大鱼只有可能是每个区间中最小的数字,因为不然,那么这个区间中最小的数字乘以二一定比它自己大.这个东西就很好维护了.

Example6(称球游戏)

给定$n$个球(其中有一个次品球,重量和其它球不一样)和一架天平,求最少通过多少次操作才能找到这个球.

我们通过这个游戏来引入信息论和判定树作为一个构造下界的工具.

首先引入一套语言体系来简化文字:

$S$表示标准球.
$< A , B >$表示称量集合$A$和集合$B$,$< A , B > = 0$表示平衡,$< A , B > = A$表示$A$较重,$< A , B > = B$表示$B$较重.

信息论

如果一个随机变量$x$有$n$种取值,出现概率分别为$p_1 , p_2 , \cdots , p_n$,则其熵为$H ( x ) = f ( p_1 , p_2 , \cdots , p_n ) = \sum{ C p_i \ln \frac{ 1 }{ p_i } }$,$C$为正整数,通常取$1$.(事实上这里的定义与真正的信息论的定义有一定的差别,不过原理是类似的,这里简化了一些.)

定理1:在得到关于随机变量$x$的一个熵为$h$的信息后,$x$的熵会减少$h$.

定理2:当一个随机变量的各种取值概率相等时,它的熵最大.

用信息论估计一下称球游戏的上界,如果我们已知次品轻重,由于一共有$n$个球,每个球等概率成为次品,因此总熵是$\ln n$,每称一次能得到的信息有三种:平衡,左边重,右边重,因此称一次能得到的熵是$\ln 3$,也就是说我们至少要猜$\frac{ \ln n }{ \ln 3 } = \log_3 n$次.如果我们不知道次品的轻重,那么至少要猜$\frac{ \ln 2 n }{ \ln 3 } = \log_3 2 n$次.

这就是称球游戏的信息论下界,接下来我们要做的无非就是证明这个下界能否取得到.

判定树

我们考虑将称量的决策树建立出来,每个叶子节点表示我们得到的答案,每个非叶子节点代表一次称量,每个非叶子节点有三个儿子,分别表示如果称量的结果是左偏/右偏/平衡时,接下来的策略.显然判定树的深度就是最坏情况下称量的次数.

$n$个叶子的树的最小深度是$\lceil \log_3 n \rceil$,这得出和信息论一样的下界估计(信息论的结论好像就是拿哈夫曼树证明的,不太懂).

子问题1(已知次品重量)

不妨假设$f ( n )$表示有$n$个球的最少次数,注意到$f ( 3 ) = 1$.

根据信息论,$f ( n ) \geq \lceil \log_3 n \rceil$,下面证明等号成立:

首先考虑证明$f ( 3^m ) = m$,$m = 1$时已经得证.$m > 1$时,考虑将所有球分成等数量的三份,称量其中两份.由于已知次品重量,这一次就可以找到次品在哪一份中,因此$f ( 3^m ) \leq f ( 3^{ m - 1 } ) + 1$.综合信息论下界$f ( 3^m ) \geq m$,我们不难得出以上结论.至于$n \ne 3^m$的情况,我们类似这个过程按照$n \bmod 3$的值讨论一下即可,于是有$f ( n ) \leq f ( \lceil \frac{ n }{ 3 } \rceil ) + 1$.

子问题2(不知次品轻重,已有一个标准球,需知道次品轻重)

根据信息论下界,$f ( n ) \geq \lceil \log_3 2 n \rceil$.

比起上面的问题,这个问题在于:如果我们称量不平衡,是不知道次品球在两堆中的哪一堆的.但我们思考到:虽然我们不知道在哪一堆,但我们得到了一个额外的信息:如果它在哪一堆,它的重量我们也就知道了.

下面证明引理:

引理

有两堆球,第一堆有$n$个球,第二堆有$m$个,已知其中有一个次品,并且次品如果在第一堆中只可能是重球,在第二堆中只可能是轻球.设此时的称量次数是$g ( n , m )$,则$g ( n , m ) = \lceil \log_3 ( n + m ) \rceil$.

先证明信息论下界,不难发现仍然是$g ( n , m ) = \lceil \log_3 ( n + m ) \rceil$.

首先不难发现,$g ( 1 , 0 ) = g ( 0 , 1 ) = 0 , g ( 1 , 1 ) = g ( 2 , 0 ) = g ( 0 , 2 ) = 1$.

仍然使用数学归纳,假设$n + m < k ( k \geq 3 )$的时候成立,我们接下来证明$n + m = k$的时候仍然成立.

情况1

若$n = 3 p , m = 3 q$,我们将$n$分成等数量的三堆:$A_1 , B_1 , C_1$,将$m$分成等质量的三堆$A_2 , B_2 , C_2$.

接下来称量$\langle A_1 + A_2 , B_1 + B_2 \rangle$.

如果$\langle A_1 + A_2 , B_1 + B_2 \rangle = 0$,那么答案在$C_1 \cup C_2$中,此时有$g ( n , m ) = g ( \frac{ n }{ 3 } , \frac{ m }{ 3 } ) + 1$.
如果$\langle A_1 + A_2 , B_1 + B_2 \rangle = A_1 + A_2$,由于若次品在$A_2$中,那么它不可能是重球,因此次品不可能在$A_2$中,同理不可能在$B_1$中,只可能在$A_1 \cup B_2$中,此时有$g ( n , m ) = g ( \frac{ n }{ 3 } , \frac{ m }{ 3 } ) + 1$.
$\langle A_1 + A_2 , B_1 + B_2 \rangle = B_1 + B_2$,同理.

此时数学归纳成立.

情况2

$n = 3 p + 1 , m = 3 q + 2$.此时我们将第一堆分成$A_1 ( p ) , B_1 ( p ) , C_1 ( p + 1 )$,将第二堆分成$A_2 ( q + 1 ) , B_2 ( q + 1 ) , C_2 ( q )$,然后$\langle A_1 + A_2 , B_1 + B_2 \rangle$,接下来和情况1一样,于是有$g ( n , m ) = \max \{ g ( p , q + 1 ) , g ( p + 1 , q ) \} = \lceil \log_3 \frac{ n + m }{ 3 } \rceil + 1$.

同理,当$n , m \bmod 3$的值是其它组合的时候,也都可以类似操作.引理得证.

由此引理得证.

回到原问题,进行数学归纳,我们继续来讨论$n \bmod 3$的值.

情况1

当$n = 3 p$时,直接分成$A ( p ) , B ( p ) , C ( p )$,然后$\langle A , B \rangle$.如果平衡则接下来需要$f ( p ) = \lceil \log_3 2 p \rceil$次,不然根据引理,需要$\lceil \log_3 ( p + p ) \rceil$次,因此$f ( n ) = \lceil \log_3 2 p \rceil + 1 = \lceil \log_3 6 p \rceil = \lceil \log_3 2 n \rceil$.

情况2

当$n = 3 p + 1$时,一种自然的想法是分成$A ( p + 1 ) , B ( p ) , C ( p )$,但是这种想法是错误的!我们考虑判定树,这种情况下,所有的叶子被分成了$2 p + 2 , 2 p , 2 p$,这显然是不优秀的.正确的做法是分成$A = \{ S , 1 , \cdots p \} , B = \{ p + 1 , \cdots 2 p + 1 \} , C = \{ 2 p + 2 , \cdots 3 p + 1 \}$.由于存在标准球,此时如果$\langle A , B \rangle = A or B$,那么转化成$g ( p , p + 1 ) = \lceil \log_3 ( 2 p + 1 ) \rceil$,不然转化成$f ( p ) = \lceil \log_3 2 p \rceil$.

剩下的情况也都类似,该问题解决.

子问题3(不知次品轻重,无标准球,需知道次品轻重)

考虑在第一次称量后,无论结果如何都会得到一个标准球,因此后面的问题都等价于子问题2,只需考虑第一次操作.再思考一下不难发现,在子问题2中,只有$n \bmod 3 = 1$的时候才会需要用到标准球,因此只有这里需要多一步.拟合一下函数,可以得到该问题$f ( n ) = \lceil \log_3 ( 2 n + 2 ) \rceil$.

子问题4(不知次品轻重,已有一个标准球,无需知道次品轻重)

这个问题复杂一些,而且难以估计下界.但我们可以用一下最优化dp来估计下界.

首先假设有无穷个标准球,我们每次将$a$个球放左边,$b$个球放右边,$a \leq b$,在左边补上$b - a$个标准球.

如果天平不平衡,转化为引理问题(因为此时找到次品是谁必然知道它的轻重),因此需要$\lceil \log_3 ( a + b ) \rceil + 1$步.
如果天平平衡,需要$f ( n - a - b ) + 1$步.

我们有$f ( n ) = \min_{ a , b } \{ \max \{ f ( n - a - b ) , \lceil \log_3 ( a + b ) \rceil \} \} + 1$.

注意到接下来的步数只与$a + b$有关,取$b - a \leq 1$,于是一个标准球已经够用了.

构造方程后手算几项,注意到$f ( n ) = \lceil \log_3 ( 2 n - 1 ) \rceil$.

接下来归纳法就简单了,只需要对于$n \bmod 3$的余数讨论一下,然后再讨论一下$a$的取值即可.

Example7(Ucup 3rd Stage 8 H)

每次可以询问一个区间,交互库返回这个区间中的次大元素所在位置,求$n$所在位置.要求询问次数$\leq \lceil 1 . 5 \log_2 n \rceil$,询问区间总长度$\leq 3 n$.

一个自然的想法是先问一下全局次大值,然后二分,但这样询问区间总长度就会爆掉.

因此考虑设$T ( n )$表示长度为$n$的,已知次大值(并且次大值)的最小次数.我们考虑每次判断一下最大值在哪边,因此把这个区间拆成两半,然后询问一下次大值所在的那一半,这样就可以判断最大值在不在那一半.

那么我们当然有方程$T ( n ) = \min_{ m < n } \{ \max \{ T ( m ) + 1 , T ( n - m ) + 2 \} \}$.

当然有$m_n \leq m_{ n + 1 }$,于是直接dp即可.

Exchange Arguments

模型1

给定$n$个元素$x_1 , . . . , x_n$,以及一个定义域为这些元素的序列,定义域为有序集合的函数$F$.求出对于所有的$n$阶排列$p$,表达式$F ( \{ x_{ p_1 } , x_{ p_2 } , . . . , x_{ p_n } \} )$最小值.

事实上会发现一些NPC问题也可以直接转化为这个模型,但是并无贪心解.我们接下来考虑这个模型内哪些问题是有贪心解的.

Example1(国王游戏)

给定$n$个二元正整数对$( a_i , b_i )$,将它们按照任意顺序排成一列.定义排成一列的代价为每个二元组的$a$乘上序列中这个二元组之后的所有二元组的$b$之和的总和,求最小代价.$n , a_i , b_i \leq 10^6$.

转化为上面的形式,也即:$F ( \{ ( a_1 , b_1 ) , . . . , ( a_n , b_n ) \} ) = \sum_{ 1 \leq i < j \leq k } a_i b_j$.

考虑调整法,令排列$( q_1 , . . . , q_n ) = ( p_1 , . . . , p_{ i - 1 } , p_{ i + 1 } , p_i , p_{ i + 2 } , . . . , p_n )$.则:

$F ( \{ ( a_{ p_1 } , b_{ p_1 } ) , . . . , ( a_{ p_n } , b_{ p_n } ) \} ) - F ( \{ ( a_{ q_1 } , b_{ q_1 } ) , . . . , ( a_{ q_n } , b_{ q_n } ) \} ) = a_{ p_i } b_{ p_{ i + 1 } } - a_{ p_{ i + 1 } } b_{ p_i }$

因而如果$a_{ p_i } b_{ p_{ i + 1 } } - a_{ p_{ i + 1 } } b_{ p_i } > 0$,则$F ( \{ ( a_{ p_1 } , b_{ p_1 } ) , . . . , ( a_{ p_n } , b_{ p_n } ) \} ) > F ( \{ ( a_{ q_1 } , b_{ q_1 } ) , . . . , ( a_{ q_n } , b_{ q_n } ) \} )$,也就是说$( p_1 , . . . , p_n )$不是最优解.因此只有满足$\forall 1 \leq i < n$,$\cfrac{ a_{ p_i } }{ b_{ p_i } } \leq \cfrac{ a_{ p_{ i + 1 } } }{ b_{ p_{ i + 1 } } }$可能是最优解.

如果一个$p$满足这样的性质,则所有$\cfrac{ a }{ b }$相等的数在排列中一定是连续的一段.而根据式子,这样的排列交换$\cfrac{ a }{ b }$相等的两个位置,是不会使答案改变的.因此直接按照$\cfrac{ a }{ b }$排序即可.

我以前所使用的调整法大概是先构造一个贪心策略,然后证明这个策略改变后一定不优秀或更劣.但是这样对于多峰函数会卡在一个局部最优解上而找不到全局最优解.但是,如果我们说不满足这个条件的一定不是最优解(可以使用调整得到更优解),我们再证明满足这个条件(即调整过程DAG的终止点)的都是最优解,继续做下去,就是很严谨的.

换句话说,我们要用调整法,就一定要证明调整过程中的DAG的零出度点是最优解.

模型通解

设给出的元素的集合为$S$,定义$S$上的一种二元比较关系$\leq$,将所有元素按照比较关系排序.在上一个问题中,不难发现以下性质:

强完全性:$\forall a , b \in S$,$a \leq b \lor b \leq a = 1$.
传递性:$\forall a , b , c \in S$,$a \leq b , b \leq c \Rightarrow a \leq c$.
$\forall a , b \in S$,如果$a \leq b$,则对于任意一个包含$\{ a , b \}$作为子段的元素序列$\{ s_1 , . . . , s_{ k - 1 } , a , b , s_{ k + 2 } , . . . , s_n \}$和$\{ s_1 , . . . , s_{ k - 1 } , b , a , s_{ k + 2 } , . . . , s_n \}$都有:$F ( \{ s_1 , . . . , s_{ k - 1 } , a , b , s_{ k + 2 } , . . . , s_n \} ) \leq F ( \{ s_1 , . . . , s_{ k - 1 } , b , a , s_{ k + 2 } , . . . , s_n \} )$.

问题满足以上性质,那么我们按照这种二元比较关系对元素排序后的答案一定是最优的.原因在于,首先这种操作构成DAG,而定义$\leq$后自然也就定义了$=$,所以DAG的零出度点自然是最优解点.

分析题目时,应该先分析第三条性质得到$\leq$的定义,然后判断是否符合前两条性质.

Example2

给定$n$个包含小写字符的字符串$s_1 , . . . , s_n$,找到一个$n$阶排列$p$,将$s_{ p_1 } , s_{ p_2 } , . . . , s_{ p_n }$顺序拼接得到$S$,使$S$的字典序最小.

令$s \leq t$当且仅当$s + t$的字典序$\leq$t+s

此时我们注意到:$s + t$的字典序小于等于$t + s$的字典序当且仅当$s^{ \infty } \leq t^{ \infty }$.原因是:不妨设$s$的长度$\leq t$的长度.若$s$不是$t$的前缀,那显然只需比较$t$的前缀和$s$的字典序即可,此时上面两个条件等价;若$s$是$t$的前缀,则我们需要比较$t$的前缀和$t$的后缀,注意到$t$的前缀还是$s$,于是需要比较$s$和$t$的后缀.类似可得.

于是这题可以使用后缀数组求任意两个字符串的后缀的最长公共前缀实现.

Example3

有$n$个箱子,第$i$个箱子有重量$w_i$和承载量$v_i$,$( w_i , v_i > 0 )$,将它们堆成一列使得每一个箱子上面的箱子总重量都不大于它的承载量.

考虑最大化$\min_{ i = 1 }^n \{ v_i - \sum_{ j = 1 }^{ i - 1 } w_j \}$,并判断是否$\geq 0$.

我们令$b_i = - ( v_i + w_i ) , a_i = - v_i$,则我们要最大化$\min \{ \sum_{ j = 1 }^{ i - 1 } b_i - \sum_{ j = 1 }^i a_i \}$.

我们接下来将证明所有形如这样的题的通法.

首先,定义$x \leq y$当且仅当$F ( \{ x , y \} ) \leq F ( \{ y , x \} )$,那么对于两个元素$( a_1 , b_1 ) , ( a_2 , b_2 )$,显然$( a_1 , b_1 ) \leq ( a_2 , b_2 )$当且仅当$\min \{ - a_1 , b_1 - a_1 - a_2 \} \geq \min \{ - a_2 , b_2 - a_1 - a_2 \}$.接下来我们证明这样的定义是满足性质的.

对于性质(3),显然成立,因为交换两个相邻位置不会对前面或后面产生影响,而前后对于这两个位置的影响也都可以抵消.

性质(1)显然成立.

再分析一下这个式子,这相当于不等式左边的两个元素都大于等于右边的最小值.我们讨论一下两种情况:

都大于等于第一个元素,则相当于$a_1 \leq a_2 \land b_1 - a_1 \geq 0$.
都大于等于第二个元素,则相当于$b_1 \geq b_2 \land b_2 - a_2 \leq 0$.

可能这里后面和$0$比较没有移项来得简洁.但是,相减的两项是同一个元素的两项,我们显然把它俩放在一类是更优秀的.

注意到需要对$b - a$的符号进行讨论:

若$sgn ( b_1 - a_1 ) > sgn ( b_2 - a_2 )$,则不等式成立.
若$sgn ( b_1 - a_1 ) = sgn ( b_2 - a_2 ) = 1$,则不等式成立当且仅当$a_1 \leq a_2$.
若$sgn ( b_1 - a_1 ) = sgn ( b_2 - a_2 ) = 0$,则不等式成立.
若$sgn ( b_1 - a_1 ) = sgn ( b_2 - a_2 ) = - 1$,则不等式成立当且仅当$b_1 \geq b_2$.

这四条中(2)和(4)的证明是显然的,(3)则是因为此时$b_1 = a_1$,$b_2 = a_2$,两条件必有一真.(1)则是因为此时满足$b_1 - a_1 > b_2 - a_2 \land sgn ( b_1 - a_1 ) \geq 0 \land sgn ( b_2 - a_2 ) \leq 0$.也就有$a_2 - a_1 > b_2 - b_1 \land b_1 \geq a_1 \land b_2 \leq a_2$.怎么着都能成立.

由此发现,对于$sgn ( b - a )$相同的类,内部排序是一定满足传递性的.

但是不同类之间并没有满足传递性,因此我们把排序条件修正为:

$\begin{aligned} ( a_1 , b_1 ) & \leq ( a_2 , b_2 ) \\ \Updownarrow \\ ( sgn ( b_1 - a_1 ) & > sgn ( b_2 - a_2 ) ) \\ \lor ( sgn ( b_1 - a_1 ) & = sgn ( b_2 - a_2 ) \land F ( \{ 1 , 2 \} ) \leq F ( \{ 2 , 1 \} ) \end{aligned}$

模型2

给定$n$个元素$x_1 , . . . , x_n$,以及一个定义域为这些元素的序列,值域为有序集合的函数$F$.求出对于给定整数$k$,所有的$n$阶排列$p$的长度为$k$的子序列,表达式$F ( \{ x_{ p_1 } , x_{ p_2 } , . . . , x_{ p_k } \} )$最小值.

如果$k = n$,则就是模型1.不然,我们考虑先选出一个大小为$k$的子集,然后使用模型1.不难发现,我们最后取出的$\{ x_{ p_1 } , x_{ p_2 } , . . . , x_{ p_k } \}$一定是$n = k$时最优解的一个子序列.这在一些情况下可以降低问题的难度.

Example

有$n$个物品,第$i$个物品有非负费用$c_i$和价值$v_i$,两个人进行如下博弈:

第一个人要么选择一个物品,付出$c_i$的代价;要么选择结束游戏.
第二个人可以选择删除这个物品,这会使博弈回到第一步,且第一个人付出的代价不会消失(这个操作最多可以进行$k$次);也可以选择不操作,此时第一个人获得$v_i$的收益,博弈结束.
第一个人的总收益为收益减去付出的所有代价,第一个人希望最大化收益,第二个人希望最小化收益.$( n \leq 1 . 5 \times 10^5 , k \leq 9 )$

注意到第一个人要么一开始就结束游戏,要么连续选择$k + 1$个,然后收益为$\min_{ i = 1 }^{ k - 1 } \{ v_{ x_i } - \sum_{ j = 1 }^i c_{ x_j } \}$(如果第一个人把一个收益很大的放在最后选,那第二个人可以直接结束游戏防止他选到).注意到这和模型1的Example3是类似的,于是我们可以先排序,然后dp出子序列,复杂度$O ( n \log n + nk )$.

构造

增量构造

Example1

平面上有$n$条直线,将整个平面划分成若干部分.求证:这些部分可以黑白染色使得两个边相邻的部分颜色不相同,并给出构造方案.

考虑数学归纳,现在已经有$n$条直线的答案,求$n + 1$条直线的答案.我们将直线加到这个平面上,并将在这条直线其中一边的部分颜色全部取反.

Example2

给定若干个角度$a_1 , \cdots , a_n \in \{ 90 \degree , 270 \degree \}$,要求构造一个$n$边形(边必须平行于坐标轴),使得其内角依次是$a_1 , \cdots , a_n$.

首先有解条件显然是判定它们的和是否是$180 \degree ( n - 2 )$.

注意到相邻的$90 \degree$和$270 \degree$无非是在原序列上修修改改,这个可以一起合并起来.不断合并就做完了.

Example3(CF1770H)

呃,简单来说就是把边界往里缩,每次找左上和右上的四个点做匹配,然后剩下的缩进去.

原题解的那个图特别清晰.

Example4(ABC232H)

放在这个模块下就好想了,剥一行一列就行.最后可能会剩个边界情况,简单讨论.

找中间状态

常见于操作可逆,想要让$S \rightarrow T$.这个时候可以找一个中间状态$A$,让$S \rightarrow A , T \rightarrow A$.

Example1

坐标系上每个整点有个灯,初始只有$( X , 0 )$亮着,每次把$( x , y )$,$( x , y + 1 )$,$( x + 1 , y )$状态反转,给出终止状态,求初始亮的点的坐标,保证有解且唯一解.

$n \leq 10^5$,坐标的绝对值均$\leq 10^{ 17 }$.

首先我们发现,如果我们上面有若干个亮点,我们一定能把他们全杀了,变到下面,但下面的亮点没办法处理.怎么办呢?

一个想法是,我们将所有的亮点全都推到一条直线$y = - inf$,然后比对.我们注意到$( X , 0 )$向下推的过程类似一个组合数递推的过程,由经典公式$\binom{ S }{ T } \equiv [ T \subseteq S ] \bmod 2$可知,我们取$inf = 2^{ 63 } - 1$即可.然后最后在这条线上一定是有一个区间是$1$,我们需要找到区间左端点,我们选择在直线上随便找到一个$1$,由于$inf$很大,大于$10^{ 17 }$,因此这一步是好找的.然后最后二分+算贡献就可以找到左端点.

这个题有个改版,$n \leq 10^4$,但是初始点可能是$( X , Y )$.

这个题怎么做呢?类似上面的,我们考虑找到两个点$( j , - inf )$和$( k , - inf )$是亮的,并且他们分别是最靠左的和最靠右的,然后我们就能反解出$X$和$Y$.而上述条件满足当且仅当$[ j - X \subseteq Y + inf ]$.

如果我们随便找一个点$( p , - inf )$满足条件,那我们接下来只需要枚举$w$,判断$( p - 2^w , - inf )$是否是亮的,这样就能找到最靠左的,同理可以找到最靠右的.

那么怎么找到这个点呢?我们二分,每次判断一个区间$[ l , r ]$中是否有亮的.这个是难以判断的,但是好判断的是,这个区间中亮的灯的数量是奇数还是偶数.因此我们拿这个判断就行,有奇数就去奇数,两个都是偶数随便去一个.

计算几何

发表于 2025-06-23 分类于 OI Waline：

二维计算几何

参考:https://www.luogu.com.cn/blog/command-block/ji-suan-ji-he-suan-fa-hui-zong.

这一部分比较常用,知识点也比较简单,会主要聚焦于写法.

基本函数

eps

1	const double eps=1e-10

浮点数计算存在误差,因此大部分时候不能直接进行大小是否相等的判断,我们需要通过规定精度来减少这种误差.

sign

inline int sign(double x){
if(x<eps&&-x<eps)return 0;
if(x>eps)return 1;
return -1;
}

用于判断一个浮点数是正数还是负数.

myabs

inline double myabs(double x){
if(sign(x)==-1)return -x;
return x;
}

用来求绝对值.

mysqr

1
2
3

inline double mysqr(double x){
return x*x;
}

用来求平方.

Point/Vector

struct Point{
double x,y;
Point(double X,double Y){
x=X;y=Y;
}
inline double len(){//判断到原点的距离
return std::sqrt(x*x+y*y);
}
inline int que(){//判断点的象限
if(sign(x)== 1&&sign(y)== 1)return 1;
if(sign(x)==-1&&sign(y)== 1)return 2;
if(sign(x)==-1&&sign(y)==-1)return 3;
return 4;
}
};
inline Point operator +(const Point &A,const Point &B){
return Point(A.x+B.x,A.y+B.y);
}
inline Point operator -(const Point &A,const Point &B){
return Point(A.x-B.x,A.y-B.y);
}
inline Point operator *(const double &c,const Point &A){
return Point(c*A.x,c*A.y);
}
inline Point operator *(const Point &A,const double &c){
return Point(c*A.x,c*A.y);
}
inline Point operator /(const Point &A,const double &c){
return Point(A.x/c,A.y/c);
}
inline double dist(const Point &A,const Point &B){
return std::sqrt(mysqr(A.x-B.x)+mysqr(A.y-B.y));
}

存储基本的点的信息.也可以看作一个二维向量.

向量内积

1
2
3

inline double operator *(const Point &A,const Point &B){
return A.x*B.x+A.y*B.y;
}

也就是$\vec{ a } \cdot \vec{ b } = | \vec{ a } | | \vec{ b } | \cos \theta = x_a x_b + y_a y_b$.也就等于$\vec{ a }$在$b$上的投影与$\vec{ b }$的模长的乘积.

内积可以用来判断夹角:

如果$\vec{ a } \cdot \vec{ b } = 0$,则说明$\vec{ a } \bot \vec{ b }$.
如果$\vec{ a } \cdot \vec{ b } > 0$,则说明$\vec{ a }$和$\vec{ b }$正方向的夹角小于$90 \degree$.
如果$\vec{ a } \cdot \vec{ b } < 0$,则说明$\vec{ a }$和$\vec{ b }$正方向的夹角大于$90 \degree$.

两个向量同时旋转相同角度,其内积结果不变.

向量叉积

1
2
3

double operator ^(const Point &A,const Point &B){
return A.x*B.y-B.x*A.y;
}

也就是$\vec{ a } \times \vec{ b } = x_a y_b - y_a x_b$.也就等于$\vec{ a } , \vec{ b }$两个向量张成的平行四边形(有向)的面积.

叉积可以用来判断方向:

如果$\vec{ a } \times \vec{ b } = 0$,说明二者共线.
如果$\vec{ a } \times \vec{ b } < 0$,说明从$\vec{ a }$到$\vec{ b }$的方向是顺时针.
如果$\vec{ a } \times \vec{ b } > 0$,说明从$\vec{ a }$到$\vec{ b }$的方向是逆时针.

向量旋转

//插入Point内部
inline Point rotate(double theta){
double st=std::sin(theta),double ct=std::cos(theta);
return Point(x*ct-A.y*st,A.x*st+A.y*ct);
}

也就是将这个竖向量乘左乘旋转矩阵$\begin{bmatrix}\cos \theta & - \sin \theta \ \sin \theta & \cos \theta\end{bmatrix}$.

Line

struct Line{
Point a,b;
double len(){
return dist(a,b);//计算线段长度,直线和射线基本没用
}
};
bool onl0(const Point &A,const Line &L){
return sign((A-L.a)^(A-L.b))==0;
}//判断点是否在直线上
bool onl2(const Point &A,const Line &L){
return (sign((A-L.a)^(A-L.b))==0)&&
(sign(A.x-std::min(L.a.x,L.b.x))>=0)&&
(sign(A.x-std::max(L.a.x,L.b.x))>=0)&&
(sign(A.y-std::min(L.a.y,L.b.y))>=0)&&
(sign(A.y-std::max(L.a.y,L.b.y))<=0);

}//判断点是否在线段上

用来维护直线/射线/线段的基本信息.

判断线段相交

bool isinter(const Line &L1,const Line &L2){
if(std::max(L1.a.x,L1.b.x)<std::min(L2.a.x,L2.b.x))return 0;
if(std::max(L2.a.x,L2.b.x)<std::min(L1.a.x,L1.b.x))return 0;
if(std::max(L1.a.y,L1.b.y)<std::min(L2.a.y,L2.b.y))return 0;
if(std::max(L2.a.y,L2.b.y)<std::min(L1.a.y,L1.b.y))return 0;
if(((L1.a-L2.b)^(L2.a-L2.b))*((L1.b-L2.b)^(L2.a-L2.b))<0)return 0;
if(((L2.a-L1.b)^(L1.a-L1.b))*((L2.b-L1.b)^(L1.a-L1.b))<0)return 0;
return 1;
}

前四行被称为快速排斥实验,后两行被称为跨立实验,也就是相交的两线段,对于其中一个线段而言,它的两个端点必然在另一个线段的两侧.但我们注意到共线线段也会通过跨立实验,因此拿快速排斥实验来判掉这种情况.

注意,线段交点不同于直线交点,两条共线的交点是有可能在端点上的.这个需要特判一下.

当然一般判断线段是否相交可以直接求直线交点,然后判断在不在线段上.

求直线交点

Point inter(const Line &L1,const Line &L2){
double ls=(L1.b-L1.a)^(L2.a-L1.a);
double rs=(L1.b-L1.a)^(L2.b-L1.a);
return L2.a+(L2.b-L2.a)*ls/(ls-rs);
}

原理在于,画一下$x_{ L_1 } , x_{ L_2 } , y_{ L_1 } , y_{ L_2 }$围成的四边形,计算面积后用等高不等底计算.注意$ls$和$rs$所代表的面积一正一负(不一定谁是正),因此需要减一下.

点到线的最短距离

inline double disl0(const Point &A,const Line &L){
return myabs(((L.a-A)^(L.b-A))/dis(L.a,L.b));
}
inline double disl2(const Point &A,const Line &L){
if(sign((A-L.a)*(L.b-L.a))<0)return dist(A,L.a);
if(sign((A-L.b)*(L.a-L.b))<0)return dist(A,L.b);
return disl0(A,L);
}

直线好做,直接算垂线段长度,用面积除以底长.

线段用点积判一下夹角即可.

凸多边形面积

利用叉乘,任取平面上一点$O$,则$S = \frac{ 1 }{ 2 } \sum_{ i = 1 }^n \overrightarrow{ OP_i } \times \overrightarrow{ OP_{ i + 1 } }$.证明的话考虑分$O$在内部和$O$在外部两种情况分类讨论.注意此时的$P$必须逆时针排列.

另外有皮克定理:在一个平面直角坐标系内,以整点为顶点的简单多边形(任两边不交叉),它内部整点数为$a$,它的边上(包括顶点)的整点数为$b$,则它的面积$S = a + \frac{ b }{ 2 } - 1$.

基本算法

排序算法

极角排序

定义原点$O$并建立坐标系,所有点按照和$O$所连直线与$x$轴正方向的夹角排序.

极角排序通常使用叉乘来实现,因为叉乘可以快速计算两个向量的方向.但是注意到需要先判断象限,再判断叉乘.

bool cmp(Point A,Point B){//判断A能否在B前面
A=A-O,B=B-O;//O=(0,0)的时候可以省略
if(A.qua()!=B.qua()){
return A.qua()<B.qua();
}
if(sign(A^B)==0)return A.x<B.x;
return sign(B^A)==1;
}

水平序排序

bool cmp(Point A,Point B){
if(sign(A.x-B.x)==0)return sign(A.y-B.y)==-1;
return sign(A.x-B.x)==-1;
}

也就是$x$相同比$y$,否则比$x$.

二维凸包

定义

包住平面上某个点集的周长最小的简单多边形,一定是凸多边形.

实现

用水平序排序,然后从左往右扫一遍得到上凸壳,从右往左扫一遍得到下凸壳.

用一下以下函数:

inline bool anticlock(const Point &A,const Point &B,const Point &C){
return sign((A-B)^(B-C))==-1;
}
inline bool isline(const Point &A,const Point &B,const Point &C){
return sign((A-B)^(B-C))==0;
}

前者判断是否$ABC$三点是一个上凸的(注意$ABC$三点横坐标应该不降).后者判断三点共线.

旋转卡壳

定义

定义凸包上的对踵点对,也就是拿两条平行直线卡着凸包转,这两条直线会卡住凸包的两个点,这些点对组成的集合就是对踵点对集合.

实现

逆时针枚举边,然后看对面有什么被卡住了.由于凸包的凸性,在边逆时针转的时候,另一边的对踵点也会逆时针转.只要找到距离这条边所在直线最远的点即可.但这样的点可能有俩.可以简单特判,也可以加上微小随机扰动量使得这种情况可以忽略.

闵可夫斯基和

一般只讨论凸包的闵可夫斯基和.

定义

两个区域$A , B$的闵可夫斯基和定义为$\{ a + b \mid a \in A , b \in B \}$.

实现

事实上,新的区域所形成的凸包,一定是原本$A , B$的凸包的边按照某种顺序连接起来得到的结果.

我们考虑旋转一下$A , B$,使得$B$有一条边成为最右边的直上直下的一条边,然后考虑答案区域的最右边的边,这条边一定是$B$这个边加上$A$的最右边的点.这样这条边必定还在最终的凸包上.就算$A$最右边的是一条边,你也会发现最终的凸包最右边也一定是由$A$的这条边和$B$的这条边拼起来的.

显然,逆时针转一遍整个凸壳,将每条边改为向量(按照逆时针转的方向)然后极角排序,最后顺次链接就是答案.

半平面交

定义

定义半平面为满足$ax + by + c > 0$或$ax + by + c \geq 0$的点对$( x , y )$组成的集合,感性理解就是一条直线的一侧.

实现

首先直线不好描述左右侧,我们把直线改成向量,这样方便描述左右侧.并不妨假设所有的向量所表示的半平面在向量的左侧.如果两条向量方向相同,则取更靠左的那一条,也就是所在直线截距更大的那个,另一个直接删了就是了.当然你不想删可以把那个废物放前面,这样根据下面的操作过程中它会被弹掉.

我们这么实现:按照上面的顺序一个一个插入,维护一个单调队列.如果前两条向量的交点不在当前这条向量的控制范围,不难发现上一条向量是废物,弹掉它.这样做到最后,队首和队尾可能都有一些废物向量,把它们判掉弹掉即可.

三维计算几何

这一部分知识点比较困难,而几乎用不到,因此只讲简单知识点,就当是高中立体几何知识补档!

基本概念

直线

使用直线的方向向量$\vec{ s } = ( n , m , p )$和直线上一点$M_0 = ( x_0 , y_0 , z_0 )$.那么方程显然为:

$\frac{ x - x_0 }{ n } = \frac{ y - y_0 }{ m } = \frac{ z - z_0 }{ p }$

如果换元,我们还有参数方程:

$\begin{cases} x = x_0 + nt \\ y = y_0 + mt \\ z = z_0 + pt \end{cases}$

平面

使用平面上的一点$P_0 ( x_0 , y_0 , z_0 )$和该平面的法向量$\vec{ n }$来表示一个平面,不妨设$\vec{ n } = ( A , B , C )$,则该平面的方程显然为:

$A ( x - x_0 ) + B ( y - y_0 ) + C ( z - z_0 ) = 0$

如果我们令$D = - ( Ax_0 + By_0 + Cz_)$,那么平面方程为:

$Ax + By + Cz + D = 0$

夹角

两直线夹角.

直接求方向向量的夹角,然后取正值.

对于方向向量分别是$\vec{ s_1 } = ( n_1 , m_1 , p_1 ) , \vec{ s_2 } = ( n_2 , m_2 , p_2 )$,也就有$\varphi = \arccos ( \frac{ | \vec{ s }_1 \cdot \vec{ s }_2 | }{ | \vec{ s }_1 | | \vec{ s }_2 | } ) \\$.

直线与平面的夹角

同样使用向量,不妨设方向向量$\vec{ s } = ( n , m , p )$,法向量$\vec{ f } = ( a , b , c )$,那么$\varphi = \arcsin ( \frac{ | \vec{ s } \cdot \vec{ f } | }{ | \vec{ s } | | \vec{ f } | } )$.

另外,由上面这个式子,不难得到一些特殊情况下的判定标准:

若直线与平面平行,则$am + bn + cp = 0$.
若直线与平面垂直,则$\frac{ a }{ m } = \frac{ b }{ n } = \frac{ c }{ p }$.注意这里分母可能除以$0$,我们实际上应该是三个形如$a = mt$的参数方程,这里简化了.

交点

联立方程硬解.

基本定理

参考:https://zhuanlan.zhihu.com/p/401766934

三余弦定理(最小角定理)

这个定理说明直线与平面的夹角,是所有包含直线的平面与这个平面形成的夹角中最小的那一个.并且偏移量决定了差距.

三正弦定理(最大角定理)

这个定理说明二面角是另一个平面上的直线与平面的夹角中最大的那个,并且偏移量决定了差距.

组合数学

发表于 2025-06-23 分类于具体数学 Waline：

二项式系数

上升幂和下降幂

定义下降幂$x^{ \underline{ k } } = \prod_{ i = 0 }^{ k - 1 } ( x - i ) = \frac{ x ! }{ ( x - k ) ! }$.

定义上升幂$x^{ \overline{ k } } \prod_{ i = 0 }^{ k - 1 } ( x + i ) = \frac{ ( x + k - 1 ) ! }{ ( x - 1 ) ! }$.

上升幂和下降幂的定义是可以引申到复数域的.

例如我们有加倍公式:$r^{ \underline{ k } } ( r - 0 . 5 )^{ \underline{ k } } = \cfrac{ ( 2 r )^{ \underline{ 2 k } } }{ 2^{ 2 k } } , k \in \mathbb{ N }$.

他们之间存在转换:$x^{ \underline{ n } } = ( - 1 )^n ( - x )^{ \overline{ n } }$.

同时存在大小关系:$x^{ \underline{ n } } \leq x^n \leq x^{ \overline{ n } }$,其中$0 \leq n < x$.

二项式系数的定义

考虑令$\binom{ n }{ m }$表示从一个大小为$n$的子集中选出大小为$m$的子集的方案数.第一次有$n$个选择,第二次有$n - 1$个选择……第m次有$n - m + 1$个选择.而由于可能可以选择重复的,但一个排列被重复选择的次数显然是$m !$,因此显然有$\binom{ n }{ m } = \cfrac{ n^{ \underline{ m } } }{ m ! }$.

如果我们把它的定义拓展到复数域,我们有:

$\binom{ r }{ k } = \begin{cases}\cfrac{ r^{ \underline{ k } } }{ k ! } & k \geq 0 \ 0 & k < 0\end{cases} , r \in \mathbb{ C } , k \in \mathbb{ Z }$.

值得一提的是,如果我们这么定义,本质上其实是把$\binom{ r }{ k }$看作了一个关于$r$的$k$次多项式.

另外根据定义,$r \in \mathbb{ Z } \land r < k$时,该公式给出$0$.

值得一提的是,为了使二项式系数在面对$0$的时候更加简洁,通常直接定义$0 ! = 1 , 0^0 = 1$.

另外不难发现$\binom{ 2 n }{ n }$是所有$\binom{ 2 n }{ k }$中最大的.事实上我们有Wallis公式:$\lim_{ n \rightarrow \infty } \frac{ ( \frac{ 2^{ 2 n } }{ \binom{ 2 n }{ n } } )^2 }{ 2 n + 1 } = \frac{ \pi }{ 2 }$.

基本的二项式恒等式

阶乘展开式:$\binom{ n }{ k } = \cfrac{ n ! }{ k ! ( n - k ) ! } , n , k \in \mathbb{ N } , n \geq k \\$.

证明根据定义是显然的.

对称恒等式:$\binom{ n }{ k } = \binom{ n }{ n - k } , n \in \mathbb{ N } , k \in \mathbb{ Z } \\$.

根据$( 1 )$,$0 \leq k \leq n$时是显然的.而其他情况两边都会给出$0$,因此也是成立的.

吸收恒等式:$\binom{ r }{ k } = \cfrac{ r }{ k } \binom{ r - 1 }{ k - 1 } , k \in \mathbb{ Z } \land k \ne 0 \\$.

证明根据定义是显然的.

吸收恒等式的变式:$k \binom{ r }{ k } = r \binom{ r - 1 }{ k - 1 } , k \in \mathbb{ Z } \\$.

根据$( 3 )$,只需要验证$k = 0$的情况即可,也是显然的.

相伴恒等式:$( r - k ) \binom{ r }{ k } = r \binom{ r - 1 }{ k } , k \in \mathbb{ Z } \\$.

证明如下:

$\begin{aligned} ( r - k ) \binom{ r }{ k } & = ( r - k ) \binom{ r }{ r - k } \\ & = r \binom{ r - 1 }{ r - k - 1 } \\ & = r \binom{ r - 1 }{ k } \end{aligned}$

问题在于:我们在上述描述中并未提到$r$的范围,但是推导过程要求$r \in \mathbb{ N }$.不过,我们已经说明了二项式系数是关于$r$的$k$次多项式,因此只需要有$k + 1$个$r$满足这个公式即可.而根据推导过程显然有无限个$r$满足,因此这个公式对$r \in \mathbb{ C }$也是成立的.

不过事实上,直接用吸收恒等式就可以证明:

$\begin{aligned} k \binom{ r }{ k } & = r \binom{ r - 1 }{ k - 1 } \\ ( r - k ) \binom{ r }{ r - k } & = r \binom{ r - 1 }{ r - k - 1 } \\ ( r - k ) \binom{ r }{ k } & = r \binom{ r - 1 }{ k } \end{aligned}$

加法公式:$\binom{ r }{ k } = \binom{ r - 1 }{ k } + \binom{ r - 1 }{ k - 1 } , k \in \mathbb{ Z } \\$.

证明可以使用定义,也可以先用$r \in \mathbb{ N }$的情况给出组合意义,再使用多项式推理法证明.

$\binom{ r }{ m } \binom{ m }{ k } = \binom{ r }{ k } \binom{ r - k }{ m - k } , n , k \in \mathbb{ Z } \\$.

证明可以使用组合意义和多项式推理法.

平行求和法:$\sum_{ k \leq n } \binom{ r + k }{ k } = \binom{ r + n + 1 }{ n } , n \in \mathbb{ N } \\$.

我们不妨考虑不断使用加法公式:

$\binom{ r + n + 1 }{ n } = \binom{ r + n }{ n } + \binom{ r + n }{ n - 1 } = \binom{ r + n }{ n } + \binom{ r + n - 1 }{ n - 1 } + \binom{ r + n - 1 }{ n - 2 } = . . . \\$,最终下标会减成负数,这样后面的项就全都是$0$了.

也可以考虑组合意义:如果$r \in \mathbb{ N }$,那么我们考虑从右到左第一个没有被选上的数,假设它是$r + k + 1$,那么在它右边的数全部选择了,一共是$n - k$个数,而还需要在左边的$r + k$中选择$k$个数.

上指标求和法:$\sum_{ 0 \leq k \leq n } \binom{ k }{ m } = \binom{ n + 1 }{ m + 1 } , n , m \in \mathbb{ N } \\$.

可以组合意义解释:我们不妨假设选的最大数是$k + 1$,接下来就还需要在$[ 1 , k ]$中选择$m$个.

如果我们将这个公式两边同时乘以$m !$,我们可以得到公式:$\sum_{ 0 \leq k \leq n } k^{ \underline{ m } } = \cfrac{ ( n + 1 )^{ \underline{ m + 1 } } }{ m + 1 } , n , m \in \mathbb{ N } \\$,这也就是有限微积分的公式中的一个.

二项式定理:$( x + y )^r = \sum_{ k } \binom{ r }{ k } x^k y^{ r - k } , r \in \mathbb{ N } \\$.

可以使用组合意义证明.

二项式定理有一些有用的特殊情况:

$\begin{aligned} \sum_{ 0 \leq k \leq n } \binom{ n }{ k } & = 2^n , n \in \mathbb{ N } \\ \end{aligned}$

在二项式定理中令$x = y = 1$即可证明.

$\begin{aligned} \sum_{ 0 \leq k \leq n } ( - 1 )^k \binom{ n }{ k } & = 0^n = [ n = 0 ] , n \in \mathbb{ N } \\ \end{aligned}$

在二项式定理中令$x = - 1 , y = 1$即可证明,值得一提的是,当$n = 0$的时候这个式子给出$1$,并在其他情况下给出$0$,这个式子是二项式反演的基础.

三项式定理:$( x + y + z )^n = \sum_{ 0 \leq a , b , c \leq n } [ a + b + c = n ] \cfrac{ n ! }{ a ! b ! c ! } x^a y^b z^c , n \in \mathbb{ N } \\$.

证明与二项式定理类似.值得一提的是,$\cfrac{ n ! }{ a ! b ! c ! } = \binom{ n }{ b + c } \binom{ b + c }{ c }$.

多项式定理:$( \sum_{ i = 1 }^m x_i )^n = \sum_{ \forall i \in [ 1 , m ] , 0 \leq a_i \leq n } [ \sum_{ i = 1 }^m a_i = n ] \cfrac{ n ! }{ \prod_{ i = 1 }^m a_i ! } \prod_{ i = 1 }^m x_i^{ a_i } , n \in \mathbb{ N } \\$.

证明与二项式定理类似.

范德蒙德卷积:$\sum_{ k } \binom{ r }{ m + k } \binom{ s }{ n - k } = \binom{ r + s }{ n + m } , n , m \in \mathbb{ Z } \\$.

证明可以使用组合意义和多项式推理法.

另外,这个式子可以直接使用生成函数证明.

范德蒙德卷积的变式:$\sum_{ k } \binom{ l }{ m + k } \binom{ s }{ n + k } = \binom{ l + s }{ l - m + n } , l \in \mathbb{ N } , n , m \in \mathbb{ Z } \\$.

有$\binom{ l }{ m + k } = \binom{ l }{ l - m - k }$,然后运用范德蒙德卷积即可得到答案.

上指标反转公式:$\binom{ r }{ k } = ( - 1 )^k \binom{ k - r - 1 }{ k } \\$.

根据定义显然.

扩展的二项式恒等式(整数范围内)

$\sum_{ k \leq m } \binom{ r }{ k } ( - 1 )^k = ( - 1 )^m \binom{ r - 1 }{ m } , m \in \mathbb{ Z } \\$.

证明如下:

$\begin{aligned} \sum_{ k \leq m } \binom{ r }{ k } ( - 1 )^k & = \sum_{ k \leq m } \binom{ k - r - 1 }{ k } \\ & = \binom{ - r + m }{ m } = ( - 1 )^m \binom{ r - 1 }{ m } \end{aligned}$

$\sum_{ - q \leq k \leq l } \binom{ l - k }{ m } \binom{ q + k }{ n } = \binom{ l + q + 1 }{ m + n + 1 } , n , m \in \mathbb{ N } , l + q \geq 0 \\$.

可以组合意义与多项式推理法证明.

$\sum_{ k } \binom{ a + b }{ a + k } \binom{ a + b }{ b + k } ( - 1 )^k = \binom{ a + b }{ a } , a , b \in \mathbb{ N } \\$.

可以数学归纳证明.

$\sum_{ k = 0 }^m \cfrac{ \binom{ m }{ k } }{ \binom{ n }{ k } } = \cfrac{ n + 1 }{ n + 1 - m } , n , m \in \mathbb{ N } , n \geq m \\$.

我们有$\binom{ n }{ m } \binom{ m }{ k } = \binom{ n }{ k } \binom{ n - k }{ m - k } \\$,两边同时除以$\binom{ n }{ m } \binom{ n - k }{ m - k } \\$,于是我们得到了$\cfrac{ \binom{ m }{ k } }{ \binom{ n }{ k } } = \cfrac{ \binom{ n - k }{ m - k } }{ \binom{ n }{ m } } \\$.

有:

$\begin{aligned} \sum_{ k = 0 }^m \cfrac{ \binom{ m }{ k } }{ \binom{ n }{ k } } & = \sum_{ k = 0 }^m \cfrac{ \binom{ n - k }{ m - k } }{ \binom{ n }{ m } } \\ & = \cfrac{ 1 }{ \binom{ n }{ m } } \sum_{ k = 0 }^m \binom{ n - k }{ m - k } \\ & = \cfrac{ 1 }{ \binom{ n }{ m } } \sum_{ k = 0 }^m \binom{ n - m + k }{ k } \\ & = \cfrac{ \binom{ n + 1 }{ m } }{ \binom{ n }{ m } } \\ & = \cfrac{ n + 1 }{ n + 1 - m } \end{aligned}$

$( - 1 )^m \binom{ - n - 1 }{ m } = ( - 1 )^n \binom{ - m - 1 }{ n } , n , m \in \mathbb{ N } \\$.

根据上指标反转公式,这个公式两边都等于$\binom{ n + m }{ m } \\$.

$\sum_{ k \leq m } \binom{ r }{ k } ( \cfrac{ r }{ 2 } - k ) = \cfrac{ m + 1 }{ 2 } \binom{ r }{ m + 1 } , m \in \mathbb{ Z } \\$.

可以使用归纳法证明这个公式.

$\sum_{ k \leq m } \binom{ m + r }{ k } x^k y^{ m - k } = \sum_{ k \leq m } \binom{ - r }{ k } ( - x )^k ( x + y )^{ m - k } , m \in \mathbb{ Z } \\$.

不妨令左边的值为$S_m$,我们有:

$\begin{aligned} S_m & = \sum_{ k \leq m } \binom{ m + r }{ k } x^k y^{ m - k } = \sum_{ k \leq m } \binom{ m + r - 1 }{ k } x^k y^{ m - k } + \sum_{ k \leq m } \binom{ m + r - 1 }{ k - 1 } x^k y^{ m - k } \\ & = y \sum_{ k < m } \binom{ m - 1 + r }{ k } x^k y^{ m - 1 - k } + \binom{ m + r - 1 }{ m } x^m + x \sum_{ k \leq m } \binom{ m + r - 1 }{ k - 1 } x^{ k - 1 } y^{ m - k } \\ & = ( x + y ) S_{ m - 1 } + \binom{ m + r - 1 }{ m } x^m \\ & = ( x + y ) S_{ m - 1 } + \binom{ r }{ m } ( - x )^m \end{aligned}$

左右两边满足相同递归式,通过数学归纳法不难证明二者相等.

$\sum_{ k \leq m } \binom{ m + k }{ k } 2^{ - k } = 2^m , m \in \mathbb{ N } \\$.

考虑$( 7 )$,将$x = y = 1 , r = m + 1$带入,得到:

$\begin{aligned} \sum_{ k \leq m } \binom{ 2 m + 1 }{ k } & = \sum_{ k \leq m } \binom{ m + k }{ k } 2^{ m - k } \\ 2^{ 2 m } & = \sum_{ k \leq m } \binom{ m + k }{ k } 2^{ m - k } \\ 2^m & = \sum_{ k \leq m } \binom{ m + k }{ k } 2^{ - k } \end{aligned}$

$\sum_{ k } \binom{ l }{ m + k } \binom{ s + k }{ n } ( - 1 )^k = ( - 1 )^{ l + m } \binom{ s - m }{ n - l } , l \in \mathbb{ N } , n , m \in \mathbb{ Z } \\$.

可以数学归纳证明.

$\sum_{ k \leq l } \binom{ l - k }{ m } \binom{ s }{ k - n } ( - 1 )^k = ( - 1 )^{ l + m } \binom{ s - m - 1 }{ l - n - m } , l , n , m \in \mathbb{ N } \\$.

可以数学归纳证明.

拓展的二项式恒等式(实数范围内)

$\binom{ r }{ k } \binom{ r - \cfrac{ 1 }{ 2 } }{ k } = \cfrac{ \binom{ 2 r }{ 2 k } \binom{ 2 k }{ k } }{ 2^{ 2 k } } , k \in \mathbb{ Z } \\$.

将加倍公式两边同时除以$k !^2$即可得到这个公式.

$\binom{ n - \cfrac{ 1 }{ 2 } }{ n } = \cfrac{ \binom{ 2 n }{ n } }{ 2^{ 2 n } } , n \in \mathbb{ Z } \\$.

将$( 1 )$中令$r = k = n$即可得到这个公式.

$\binom{ - \cfrac{ 1 }{ 2 } }{ n } = ( \cfrac{ - 1 }{ 4 } )^n \binom{ 2 n }{ n } , n \in \mathbb{ Z } \\$.

即$( 2 )$的变形.

$\sum_{ k } \binom{ n }{ 2 k } \binom{ 2 k }{ k } 2^{ - 2 k } = \binom{ n - \cfrac{ 1 }{ 2 } }{ \lfloor \cfrac{ n }{ 2 } \rfloor } , n \in \mathbb{ N } \\$

首先根据$( 1 )$,左边$= \sum_{ k } \binom{ \cfrac{ n }{ 2 } }{ k } \binom{ \cfrac{ n - 1 }{ 2 } }{ k } \\$,而考虑到$\cfrac{ n }{ 2 }$和$\cfrac{ n - 1 }{ 2 }$必有一个是自然数,因此可以直接用范德蒙德卷积的变形.

$\sum_{ k } \binom{ - \cfrac{ 1 }{ 2 } }{ k } \binom{ - \cfrac{ 1 }{ 2 } }{ n - k } = ( - 1 )^n , n \in \mathbb{ N } \\$.

直接使用范德蒙德卷积即可证明.

$\sum_{ k } \binom{ 2 k }{ k } \binom{ 2 n - 2 k }{ n - k } = 4^n , n \in \mathbb{ N } \\$.

由$( 5 )$和$( 3 )$不难推出.

$\sum_{ k } \binom{ n }{ k } \cfrac{ ( - 1 )^k }{ x + k } = x^{ - 1 } \binom{ x + n }{ n }^{ - 1 } , x \notin \{ 0 , - 1 , . . . , - n \} \\$.

令$f ( x ) = ( x - 1 )^{ \underline{ - 1 } }$,直接做高阶差分即可得到这个式子.

$\sum_{ k = 0 }^n \binom{ r }{ k } \binom{ r }{ n - k } ( - 1 )^k = [ n is \mathrm{ even } ] ( - 1 )^{ \cfrac{ n }{ 2 } } \binom{ r }{ \cfrac{ n }{ 2 } } \\$.

首先不难发现,$( 1 - z )^r = \sum_{ k \geq 0 } ( - 1 )^k \binom{ r }{ k } \\$.

考虑$( 1 - z )^r ( 1 + z )^r = ( 1 - z^2 )^r$.

我们有$[ z^n ] ( 1 - z )^r ( 1 + z )^r = [ z^n ] ( 1 - z^2 )^r$,不难发现即上式.

卡特兰数

卡特兰数$f_n$表示:长度为$2 n$的合法括号序列个数.

卡特兰数的前几项为$1 , 1 , 2 , 5 , 14 , 42 , 132 \cdots$.

接下来,我们通过这个定义来证明以下其他定义方式.

递归定义:$f_n = \sum_{ i = 0 }^{ n - 1 } f_i f_{ n - 1 - i }$.

不妨考虑枚举一个括号序列的第一个断点,则该括号序列应形如$( A ) B$.

考虑将其删成$A$和$B$,则$A$一定合法,因为若$A$不合法,那么这里一定不是第一个断点.

通项公式:$f_n = \frac{ 1 }{ n + 1 } C_{ 2 n }^n = C_{ 2 n }^n - C_{ 2 n }^{ n - 1 }$.

考虑平面直角坐标系,我们将’(‘认为是向右上走一单位长度,将’)’认为是向右下走一单位长度.

那么卡特兰数就相当于从$( 0 , 0 )$走到$( 2 n , 0 )$不经过第四象限的方案数.

考虑反射容斥,如果只是走到$( 2 n , 0 )$的方案数是$C_{ 2 n }^n$.

而如果到达第四象限,说明在这条这线上存在一个点$( x , - 1 )$.

考虑将$x$以后的折线以直线$y = - 1$为对称轴反转,那么终点到了$( 2 n , - 2 )$.

不难发现,任意从$( 0 , 0 )$走到$( 2 n , - 2 )$的方案一定唯一对应了一种从$( 0 , 0 )$走到$( 2 n , 0 )$的不合法方案.因为从$( 0 , 0 )$走到$( 2 n , - 2 )$一定会经过直线$y = - 1$,将后半部分对称后就是其对应方案.而从$( 0 , 0 )$走到$( 2 n , - 2 )$的方案数为$C_{ 2 n }^{ n - 1 }$.

因而$f_n = C_{ 2 n }^n - C_{ 2 n }^{ n - 1 } \\$.

而$C_{ 2 n }^n - C_{ 2 n }^{ n - 1 } = \frac{ ( 2 n ) ! }{ n ! n ! } - \frac{ ( 2 n ) ! }{ ( n - 1 ) ! ( n + 1 ) ! } = \frac{ ( 2 n ) ! }{ n ! ( n + 1 ) ! } = \frac{ C_{ 2 n }^n }{ n + 1 } \\$.

递推定义:$f_n = \frac{ 4 n - 2 }{ n + 1 } f_{ n - 1 } \\$.

使用一下上一步的通项公式:

f_n=\frac{(2n)!}{n!(n+1)!}\\

f_{n-1}=\frac{(2n-2)!}{(n-1)!(n)!}

\end{cases}\\

不难发现$f_n = \frac{ ( 2 n - 1 ) ( 2 n ) }{ n ( n + 1 ) } f_{ n - 1 } \\$.整理,得到$f_n = \frac{ 4 n - 2 }{ n + 1 } f_{ n - 1 } \\$.

换个记号,设$C_n$为卡特兰数的第$n$项,卡特兰数有一个著名的结论是$k$次卷积:

$C^{ ( k ) }_n = \sum_{ \sum_{ j = 1 }^k a_j = n } \prod C_{ a_i } = \frac{ k }{ n + k } \binom{ 2 n + k - 1 }{ n }$

我们可以这么理解它:它指的是一个长度为$n + k - 1$的括号序列,前$k - 1$个必须是左括号的方案数.为啥呢?因为这样这个括号序列必须写成$( ( ( A ) B ) C ) D$之类的形式,等价于卷积.

那么证明就很简单了,类似反射容斥,有:

$\begin{aligned} C^{ ( k ) }_n & = \binom{ 2 n + k - 1 }{ n } - \binom{ 2 n + k - 1 }{ n - 1 } \\ & = \frac{ k }{ n + k } \binom{ 2 n + k - 1 }{ n } \end{aligned}$

Example([HNOI2009]有趣的数列)

首先,如果没有第三条限制,那显然奇数位置和偶数位置互不影响,直接随便选,答案就是$\binom{ 2 n }{ n }$.

而有了限制呢,我们还是想随便选然后顺序排起来,但是这次不能排列的时候使奇数位置大于偶数位置,可以发现这就是括号序列需要满足的条件,于是答案就是卡特兰数.

至于处理,这题因为模数不是质数,需要做质因数分解来维护除法.

Example2([23省选10连测day7]b)

给定$x , n$,对$y \in [ 1 , n ]$,固定$p_x = y$做笛卡尔树的形态计数.$n \leq 5 \times 10^5$.

由于是对树的形态计数,其实根本就不在乎每个点具体的取值,只要这个取值有解就行.事实上,容易发现$a_x = y$只要满足:

$x$节点的祖先数量不超过$y - 1$个(深度小于等于$y$).
$x$节点的子树大小不超过$n - y + 1$.

发现合法不太好记,经典补集转化,然后两个不合法情况无关,分别算.

我们考虑直接算出$f_p$表示$x$的深度为$p$的答案,$g_p$表示$x$的子树大小为$p$的答案,然后就可以完成这个题.

这两部分怎么算呢?

先看深度:$x$的祖先有两种:一种在序列中在$x$的左边,一种在$x$的右边.我们设前者为$0 = l_0 < l_1 < l_2 < \cdots l_p < l_{ p + 1 } = x$,设后者为$n + 1 = r_0 > r_1 > r_2 > \cdots > r_{ q } > r_{ q + 1 } = x$.这么分类有什么用呢?我们考虑$( l_{ i - 1 } , l_{ i } )$这一段数能放在哪里,它只能是$l_{ i }$的左儿子,独立于整棵树,因此这一段的答案就是$C_{ l_i - l_{ i - 1 } - 1 }$.

记:

$\begin{aligned} L_p & = \sum_{ l } \prod_{ i = 1 }^{ p + 1 } C_{ l_i - l_{ i - 1 } - 1 } \\ R_q & = \sum_{ r } \prod_{ i = 1 }^{ q + 1 } C_{ r_{ i - 1 } - r_i - 1 } \\ \end{aligned}$

注意到这等价于卡特兰数的$k$次卷积,有:

$\begin{aligned} L_p & = C_{ x - p - 1 }^{ ( p + 1 ) } \\ R_q & = C^{ ( q + 1 ) }_{ n - x - q } \\ \end{aligned}$

此时的答案自然是$f_{ p + q + 1 } = L_p R_q \binom{ p + q }{ q }$,做卷积.

儿子怎么算呢?二叉搜索树有一个经典性质:确定根后每个点插在哪里是固定的.也就是说我们把$x$的子树从原树中删去,然后插入$x$一定会插回原位置,这是一个双射.而子树内随便做,设左子树大小为$p$,右子树大小为$q$,我们有$g_{ p + q + 1 } = C_p C_q C_{ n - ( p + q + 1 ) } = C_{ n - 1 }^{ ( 3 ) }$,同样是简单的卷积.

二项式系数的处理

通过恒等式变形求解

Example1

求$\sum_{ k = 0 }^n k \binom{ m - k - 1 }{ m - n - 1 } , n , m \in \mathbb{ N } \land m > n \\$.

这个式子乘了个系数$k$导致很难处理,一个自然的想法是使用吸收恒等式将$k$消去,然后对后面的式子使用上指标求和.

于是:

$\begin{aligned} \sum_{ k = 0 }^n k \binom{ m - k - 1 }{ m - n - 1 } & = \sum_{ k = 0 }^n m \binom{ m - k - 1 }{ m - n - 1 } - \sum_{ k = 0 }^n ( m - k ) \binom{ m - k - 1 }{ m - n - 1 } \\ & = m \sum_{ k = 0 }^{ m - 1 } \binom{ m - k - 1 }{ m - n - 1 } - ( m - n ) \sum_{ k = 0 }^m \binom{ m - k }{ m - n } \end{aligned}$

不妨令$S_m = \sum_{ k = 0 }^m \binom{ m - k }{ m - n } \\$,不难发现我们有:

$S_m = \sum_{ k = 0 }^m \binom{ k }{ m - n } = \binom{ m + 1 }{ m - n + 1 }$

于是原式$= mS_{ m - 1 } - ( m - n ) S_m = \cfrac{ n }{ m - n + 1 } \binom{ m }{ m - n } \\$.

不过事实上,我们有另一种方式来处理这个等式,我们直接将$k = \binom{ k }{ 1 }$带入:

$\begin{aligned} \sum_{ k = 0 }^n k \binom{ m - k - 1 }{ m - n - 1 } & = \sum_{ k = 0 }^n \binom{ k }{ 1 } \binom{ m - k - 1 }{ m - n - 1 } \\ & = \binom{ m }{ m - n + 1 } \\ & = \cfrac{ n }{ m - n + 1 } \binom{ m }{ m - n } \end{aligned}$

Example2

求$\sum_{ k } k \binom{ n }{ k } \binom{ s }{ k } , n \in \mathbb{ N } \\$.

第一反应仍然是使用吸收恒等式,但是注意到$n$和$s$的范围不一样,由于吸收恒等式的范围很松,因此应选择一个范围更松的数吸收,这样才能保证另一个数范围的特殊性,于是有:

$\begin{aligned} \sum_{ k } k \binom{ n }{ k } \binom{ s }{ k } & = s \sum_{ k } \binom{ n }{ k } \binom{ s - 1 }{ k - 1 } \\ & = s \binom{ n + s - 1 }{ n - 1 } \end{aligned}$

Example3

求$\sum_{ 0 \leq k } \binom{ n + k }{ 2 k } \binom{ 2 k }{ k } \cfrac{ ( - 1 )^k }{ k + 1 } , n \in \mathbb{ N } \\$.

我们有:

$\begin{aligned} \sum_{ 0 \leq k } \binom{ n + k }{ 2 k } \binom{ 2 k }{ k } \cfrac{ ( - 1 )^k }{ k + 1 } & = \sum_{ 0 \leq k } \binom{ n + k }{ k } \binom{ n }{ k } \cfrac{ ( - 1 )^k }{ k + 1 } , n \in \mathbb{ N } \\ & = \cfrac{ 1 }{ n + 1 } \sum_{ 0 \leq k } \binom{ n + k }{ k } \binom{ n + 1 }{ k + 1 }{ ( - 1 )^k } \\ & = \cfrac{ 1 }{ n + 1 } \sum_{ 0 \leq k } \binom{ - n - 1 }{ k } \binom{ n + 1 }{ k + 1 } \\ & = \cfrac{ 1 }{ n + 1 } \binom{ 0 }{ n } \\ & = [ n = 0 ] \end{aligned}$

Example4

求$\sum_{ k \geq 0 } \binom{ n + k }{ m + 2 k } \binom{ 2 k }{ k } \cfrac{ ( - 1 )^k }{ k + 1 } , n , m \in \mathbb{ N_+ } \\$.

考虑恒等式扩展的二项式恒等式(整数范围内)的$( 1 )$,我们有:

$\begin{aligned} \sum_{ k \geq 0 } \binom{ n + k }{ m + 2 k } \binom{ 2 k }{ k } \cfrac{ ( - 1 )^k }{ k + 1 } & = \sum_{ k \geq 0 } \sum_{ 0 \leq j \leq n + k - 1 } \binom{ n + k - 1 - j }{ 2 k } \binom{ j }{ m - 1 } \binom{ 2 k }{ k } \cfrac{ ( - 1 )^k }{ k + 1 } \\ & = \sum_{ 0 \leq j \leq n - 1 } \binom{ j }{ m - 1 } \sum_{ j + 1 - n \leq k , 0 \leq k } \binom{ n + k - 1 - j }{ 2 k } \binom{ 2 k }{ k } \cfrac{ ( - 1 )^k }{ k + 1 } \end{aligned}$

注意到如果$j + 1 - n \geq 0$,则$\binom{ n + k - 1 - j }{ 2 k } \\$应为$0$.所以有:

$\begin{aligned} & \sum_{ 0 \leq j \leq n - 1 } \binom{ j }{ m - 1 } \sum_{ j + 1 - n \leq k , 0 \leq k } \binom{ n + k - 1 - j }{ 2 k } \binom{ 2 k }{ k } \cfrac{ ( - 1 )^k }{ k + 1 } \\ = & \sum_{ 0 \leq j < n } \binom{ j }{ m - 1 } [ n - 1 - j = 0 ] = \binom{ n - 1 }{ m - 1 } \end{aligned}$

Example5

求$\sum_{ k = 0 }^n ( C_n^k )^2$.

$\sum_{ k = 0 }^n ( C_n^k )^2 = \sum_{ k = 0 }^n C_{ n }^k \times C_{ n }^{ n - k } = C_n^{ 2 n }$

转化为递归式/和式求解

Example1

求$Q_n = \sum_{ k \leq 2^n } \binom{ 2^n - k }{ k } ( - 1 )^k , n \in \mathbb{ N } \\$.

如果要转化为递归式的话,我们所掌握的只有加法恒等式,但加法恒等式只给出了杨辉三角中相邻两行的关系.但由于$Q_n$的式子中实际上只与$2^n$有关,我们不妨令$R_n = \sum_{ k \leq n } \binom{ n - k }{ k } ( - 1 )^k \\$,显然有$Q_n = R_{ 2^n }$.

而我们有:

$\begin{aligned} R_n & = \sum_{ k \leq n } \binom{ n - 1 - k }{ k } ( - 1 )^k + \sum_{ k \leq n } \binom{ n - 1 - k }{ k - 1 } ( - 1 )^k \\ & = \sum_{ k \leq n } \binom{ n - 1 - k }{ k } ( - 1 )^k + \sum_{ k \leq n - 1 } \binom{ n - k - 2 }{ k } ( - 1 )^{ k + 1 } \\ & = \sum_{ k \leq n - 1 } \binom{ n - 1 - k }{ k } ( - 1 )^k + \binom{ - 1 }{ n } ( - 1 )^n - ( \sum_{ k \leq n - 2 } \binom{ n - 2 - k }{ k } ( - 1 )^k + \binom{ - 1 }{ n - 1 } ( - 1 )^{ n - 1 } ) \\ & = \sum_{ k \leq n - 1 } \binom{ n - 1 - k }{ k } ( - 1 )^k - \sum_{ k \leq n - 1 } \binom{ n - 2 - k }{ k } ( - 1 )^k \\ & = R_{ n - 1 } - R_{ n - 2 } \\ & = R_{ n - 2 } - R_{ n - 3 } - R_{ n - 2 } \\ & = - R_{ n - 3 } \\ & = R_{ n - 6 } \end{aligned}$

也即$R_n$具有周期性,不难计算前几项答案,最后有$Q_n \begin{cases}1 & n = 0 \ 0 & n is \mathrm{ odd } \ - 1 & n > 0 \land n is \mathrm{ even }\end{cases}$.

Example2

求$( \sum^{ + \infty }_{ i = 0 } C^{ ik + r }_{ nk } ) \mod p$.

考虑设$f ( n , r ) = \sum^{ + \infty }_{ i = 0 } C^{ ik + r }_{ nk } \\$,则有:

$\begin{aligned} f ( n , r ) & = \sum^{ + \infty }_{ i = 0 } C^{ ik + r }_{ nk } \\ & = \sum_{ i = 0 }^{ + \infty } \sum_{ j = 0 }^k C_{ nk - k }^{ ik + r - j } \times C_k^j \\ & = \sum^k_{ j = 0 } C_k^j \sum_{ i = 0 }^{ + \infty } C_{ nk - k }^{ ik + r - j } \\ & = \sum_{ j = 0 }^k C_k^j f ( n - 1 , r - j ) \\ \end{aligned}$

整理上式,得到:$f ( n , r ) = \sum_{ j = 0 }^k C_k^j f ( n - 1 , r - j ) \\$.

于是我们得到了关于$f$的转移方程,可以矩阵加速.

利用微积分求解

Example

求$\sum_{ k = 1 }^n k^2 C_n^k$.

$\begin{aligned} ( ( 1 + x )^n ) & = ( \sum_{ k = 0 }^n C_n^k x^{ k } ) \\ ( ( 1 + x )^n ) ' & = ( \sum_{ k = 0 }^n C_n^k x^{ k } ) ' \\ n ( 1 + x )^{ n - 1 } & = \sum_{ k = 0 }^n kC_n^k x^{ k - 1 } \\ nx ( 1 + x )^{ n - 1 } & = \sum_{ k = 0 }^n kC_n^k x^{ k } \\ ( nx ( 1 + x )^{ n - 1 } ) ' & = ( \sum_{ k = 0 }^n kC_n^k x^{ k } ) ' \\ n ( ( 1 + x )^{ n - 1 } + ( n - 1 ) x ( 1 + x )^{ n - 2 } ) & = \sum_{ k = 0 }^n k^2 C_n^k x^{ k - 1 } \\ \end{aligned}$

取$x = 1$,则原式$= n ( n + 1 ) 2^{ n - 2 }$.

转化为二维平面

Example1

多次询问给定$k , r$,$\sum k \leq 2 n , r < 2 n - k$,求$\sum_{ i = 0 }^{ r } \frac{ 1 }{ 2^i } \binom{ i }{ n - k }$,.

我们把模型抽象成:在二维平面上,从$( 0 , 0 )$随机游走到$( n - k + 1 , r - n + k )$正下方(包含这个点)的概率,容易发现此时向右走了$n - k$步,总共走了$\leq r$步,然后再向右走一步保证第一次走到了$( n - k + 1 , r - n + k )$下方.

因为是概率,所以当我们已经确定这个事会发生的时候可以多走几步,不难发现这里的概率等价于走到$x + y = r + 1$这条直线时横坐标$\geq n - k + 1$的概率.枚举一下总共向上走了几步,就得到$\frac{ 1 }{ 2^{ r } } \sum_{ j = 0 }^{ r - n + k } \binom{ r + 1 }{ j }$,注意这里是$\frac{ 1 }{ 2^r }$,因为从一开始钦定了一步,因此映射过来需要多乘个$\frac{ 1 }{ 2 }$,反映射就要乘个$2$.但是这个式子还是做不了,因为$r$并不满足$\sum r \leq 2 n$.我们需要另辟蹊径.

做一下补集转化转化成走到上方的概率,这个概率就等价于$1 - \frac{ 1 }{ 2^{ r } } \sum_{ i = 0 }^{ n - k } \binom{ r + 1 }{ i }$.我们考虑暴力预处理出$f_r = \sum_{ i = 0 }^{ n } \binom{ r }{ i }$,每次删掉一个后缀的组合数就行.现在的问题在于$f$怎么做.

直接拆组合数,我们有:

$\begin{aligned} f_r & = \sum_{ i = 0 }^n \binom{ r }{ i } \\ & = \sum_{ i = 0 }^n \binom{ r - 1 }{ i - 1 } + \sum_{ i = 0 }^n \binom{ r - 1 }{ i } \\ & = 2 \sum_{ i = 0 }^n \binom{ r - 1 }{ i } - \binom{ r - 1 }{ n } \\ & = 2 f_{ r - 1 } - \binom{ r - 1 }{ n } \end{aligned}$

Lucas定理

若$p$是质数,则$C_n^m \mod p = C_{ n \mod p }^{ m \mod p } \times C_{ \lfloor \frac{ n }{ p } \rfloor }^{ \lfloor \frac{ m }{ p } \rfloor } \mod p \\$.

或者说,将$n$和$m$在$p$进制下分解,再逐位求组合数并相乘.

证明:

首先,若$i \ne 0$且$i \ne p$,$C_{ p }^i \equiv \frac{ p }{ i } C_{ p - 1 }^{ i - 1 } \equiv 0 ( \mod p ) \\$.

而根据二项式定理,$( 1 + x )^p \equiv \sum_{ i = 0 }^p C_{ p }^i x^i = 1 + x^p ( \mod p ) \\$.

令$n = k_1 p + b_1$,$m = k_2 p + b_2$,则$( 1 + x )^n = ( 1 + x )^{ k_1 p } ( 1 + x )^{ b_1 } \\$.

而$( 1 + x )^{ k_1 p } \equiv ( 1 + x^p )^{ k_1 } ( \mod p ) \\$,有$( 1 + x )^n \equiv ( 1 + x^p )^{ k_1 } ( 1 + x )^{ b_1 } \\$.

根据二项式定理,$C_n^m \bmod p$即$x^m$项的系数.

我们可以得出,$C_n^m x^m \equiv C_{ k_1 }^{ k_2 } x^{ k_2 p } C_{ b 1 }^{ b_2 } x^{ b_2 } \pmod{ p } \\$,那么有$C_a^b \equiv C_{ k_1 }^{ k_2 } C_{ b_1 }^{ b_2 } \pmod{ p } \\$.

另外,Lucas定理有一个很重要的推论是:

$\binom{ n }{ m } \equiv [ m \subseteq n ] \pmod{ 2 }$

Example1([CF1770F]Koxia and Sequence)

首先观察样例并思考,可以发现当$n$为偶数时,显然翻转整个序列就可以一一对应(除非翻转后与本身相同,但这种情况下异或值也是$0$),所以异或值为$0$.不然,我们可以翻转$a [ 2 . . . n ]$,得出答案应该是所有$a_1$的异或和.

问题在于接下来怎么做,我们考虑把按位或的那个东西容斥掉.现在问题转化为:对于所有$y ‘ \subseteq y$,求出满足$a_i \subseteq y ‘ , \sum a_i = x$时,$a_1$异或和.接下来怎么做呢?我们考虑拆位,若$2^k \subseteq y ‘$,假设$a_1$的第$k$位是$1$,然后讨论此时它对答案是否会产生贡献.

我们不难发现,第$k$位贡献是:

$[ 2^k \subseteq y ' ] \bigoplus_{ \sum a = x } [ 2^k \subseteq a_1 ] \prod_{ i = 1 }^n [ a_i \subseteq y ' ]$

这个东西看上去没办法做,但我们突然想到个事:Lucas定理的推论:$[ x \subseteq y ] \equiv \binom{ y }{ x } \pmod{ 2 }$.

所以原式化简为:

$\begin{aligned} & \binom{ y ' }{ 2^k } \sum_{ \sum a = x } \binom{ a_1 }{ 2^k } \prod_{ i = 1 }^n \binom{ y ' }{ a_i } \pmod{ 2 } \\ = & \binom{ y ' }{ 2^k } \sum_{ a_1 } \binom{ y ' - 2^k }{ a_1 - 2^k } \sum_{ \sum a = x - a_1 } \prod_{ i = 2 }^n \binom{ y ' }{ a_i } \pmod{ 2 } \\ \end{aligned}$

然后呢?不难发现后面那一串是范德蒙德卷积的形式,就可以写成:

$\begin{aligned} & \binom{ y ' }{ 2^k } \sum_{ a_1 } \binom{ y ' - 2^k }{ a_1 - 2^k } \binom{ ( n - 1 ) y ' }{ x - a_1 } \pmod{ 2 } \\ = & \binom{ y ' }{ 2^k } \binom{ ny ' - 2^k }{ x - 2^k } \pmod{ 2 } \\ = & [ 2^k \subseteq y ' ] [ ( x - 2^k ) \subseteq ( ny ' - 2^k ) ] \end{aligned}$

扩展Lucas定理

令$p = \prod p_i^{ e_i }$,那我们只要对于每个$i$求出$C_n^m \mod p_i^{ e_i }$,然后使用中国剩余定理合并即可.

那现在问题转化为要求$C_n^m \mod p^k$,其中$p \in \mathrm{ prime }$.

原式$= \frac{ n ! }{ m ! ( n - m ) ! } \mod p^k = \frac{ \frac{ n ! }{ p^x } }{ \frac{ m ! }{ p^y } \frac{ ( n - m ) ! }{ p^z } } p^{ x - y - z } \mod p^k \\$.

现在问题转化为求$\frac{ n ! }{ p^x } \mod p^k 以及 p^x \\$.

注意到:

$\begin{aligned} n ! & = \prod_{ i = 1 } i \\ & = ( \prod_{ i = wp , w \in \mathbb{ Z } } i ) ( \prod_{ i \ne wp , w \in \mathbb{ Z } } i ) \\ & = p^{ \lfloor n p \rfloor } ( \lfloor n p \rfloor ! ) ( \prod_{ i \ne wp , w \in \mathbb{ Z } } i ) \\ & \equiv p^{ \lfloor \frac{ n }{ p } \rfloor } ( \lfloor \frac{ n }{ p } \rfloor ! ) ( \prod_{ i = 1 , i \ne wp , w \in \mathbb{ Z } }^{ p^k } i )^{ \lfloor \frac{ n }{ p^k } \rfloor } ( \prod^{ n \ \bmod{ p^k } }_{ i = p^k \lfloor \frac{ n }{ p^k } \rfloor , i \ne wp , w \in \mathbb{ Z } } i ) ( \mod p^k ) \end{aligned}$

递归求解即可.

ps:

这样摆式子可能非常难以理解,我们考虑将$[ 1 , n ]$的所有数全部排成一个宽为$p^k$的矩阵.

那右边第一项就是把那些$p$的倍数的列拿出来,第二项是那些填满的行,第三项是最后没填满的一行.

斯特林数

第一类斯特林数

$n \brack k \\$:长度为$n$的排列划分成$k$个轮换的方案数.

考虑现在已经将$n - 1$个数分成了若干轮换,现在新加入第$n$个数.这个数要么和其他的数一起组成轮换,要么自己形成自环.

而由于它可以插入前面轮换的任意位置,显然$\left [ \begin{array}{ c } n \ k\end{array} \right ] = ( n - 1 ) \left [ \begin{array}{ c } n - 1 \ k\end{array} \right ] + \left [ \begin{array}{ c } n - 1 \ k - 1\end{array} \right ] \\$.

特别地,我们定义$\left [ \begin{array}{ c } 0 \ k\end{array} \right ] = [ k = 0 ] \\$.

由于所有的排列都由若干置换组成,因此我们有:$\sum_{ k = 0 }^n \left [ \begin{array}{ c } n \ k\end{array} \right ] = n !$.

第二类斯特林数

$\left \{ \begin{array}{ c } n \ k\end{array} \right \}$:将$n$个本质不同的物品划分成k个非空集合的方案数.

考虑现在已经放好$n - 1$个物品,正要放入第$n$个物品.那么这个物品要么单独放在一起,要么和其他物品放在一起.显然$\left \{ \begin{array}{ c } n \ k\end{array} \right \} = k \left \{ \begin{array}{ c } n - 1 \ k\end{array} \right \} + \left \{ \begin{array}{ c } n - 1 \ k - 1\end{array} \right \} \\$.

特别地,我们定义$\left \{ \begin{array}{ c } 0 \ k\end{array} \right \} = [ k = 0 ] \\$.

斯特林数的扩展

如果我们让斯特林数的定义式扩展到整数域,我们可以发现一个性质:${ n \brack m } ={ - m \brace - n } \\$.

基本斯特林恒等式

$x^n = \sum_{ k = 0 }^n \left \{ \begin{array}{ c } n \ k\end{array} \right \} x^{ \underline{ k } } = \sum_{ k = 0 }^n \left \{ \begin{array}{ c } n \ k\end{array} \right \} ( - 1 )^{ n - k } x^{ \overline{ k } } \\$.

证明:先考虑前半段,不妨使用数学归纳.若$x^{ n - 1 } = \sum_{ k = 0 }^{ n - 1 } \left \{ \begin{array}{ c } n - 1 \ k\end{array} \right \} x^{ \underline{ k } } \\$,我们要证

$\begin{aligned} x \sum_{ k = 0 }^{ n - 1 } \left \{ \begin{array} { c } n - 1 \\ k \end{array} \right \} x^{ \underline{ k } } & = \sum_{ k = 0 }^{ n } \left \{ \begin{array} { c } n \\ k \end{array} \right \} x^{ \underline{ k } } \\ \end{aligned}$

考虑$( x - k ) x^{ \underline{ k } } = x^{ \underline{ k + 1 } }$,所以$x \cdot x^{ \underline{ k } } = x^{ \underline{ k + 1 } } + kx^{ \underline{ k } } \\$.那么左边即:

$\begin{aligned} & \sum_{ k = 0 }^{ n - 1 } \left \{ \begin{array} { c } n - 1 \\ k \end{array} \right \} x^{ \underline{ k + 1 } } + \sum_{ k = 0 }^{ n - 1 } \left \{ \begin{array} { c } n - 1 \\ k \end{array} \right \} kx^{ \underline{ k } } \\ = & \sum_{ k = 1 }^{ n } \left \{ \begin{array} { c } n - 1 \\ k - 1 \end{array} \right \} x^{ \underline{ k } } + \sum_{ k = 1 }^{ n } \left \{ \begin{array} { c } n - 1 \\ k \end{array} \right \} kx^{ \underline{ k } } \\ = & \sum_{ k = 0 }^n \left \{ \begin{array} { c } n \\ k \end{array} \right \} x^{ \underline{ k } } \\ \\ \end{aligned}$

至于后半段,由于$x^{ \underline{ n } } = ( - 1 )^n ( - x )^{ \overline{ n } } \\$,所以$x^n = \sum_{ k = 0 }^n \left \{ \begin{array}{ c } n \ k\end{array} \right \} ( - 1 )^k ( - x )^{ \overline{ k } } \\$.

不妨用$x$来代替$- x$,我们有:

$\begin{aligned} ( - x )^n & = \sum_{ k = 0 }^n \left \{ \begin{array} { c } n \\ k \end{array} \right \} ( - 1 )^k ( x )^{ \overline{ k } } \\ x^n & = \sum_{ k = 0 }^n \left \{ \begin{array} { c } n \\ k \end{array} \right \} ( - 1 )^{ n - k } x^{ \overline{ k } } \end{aligned}$

$x^{ \overline{ n } } = \sum_{ k = 0 }^n \left [ \begin{array}{ c } n \ k\end{array} \right ] x^k \\$.
$x^{ \underline{ n } } = \sum_{ k = 0 }^n \left [ \begin{array}{ c } n \ k\end{array} \right ] ( - 1 )^{ n - k } x^k \\$.

证明:

先考虑前者,由于$( x + n - 1 ) x^k = x^{ k + 1 } + ( n - 1 ) x^k \\$,所以类似于(1)前半段的推导即可得到,后者同样可以使用下降幂和上升幂的转化来得到.

反转公式:$\sum_{ k = 0 }^n \left [ \begin{array}{ c } n \ k\end{array} \right ] \left \{ \begin{array}{ c } k \ m\end{array} \right \} ( - 1 )^{ n - k } = \sum_{ k = 0 }^n \left \{ \begin{array}{ c } n \ k\end{array} \right \} \left [ \begin{array}{ c } k \ m\end{array} \right ] ( - 1 )^{ n - k } = [ m = n ] \\$.

证明:

考虑先证明后半部分,将(3)带入(1),得到$x^n = \sum_{ k = 0 }^n \left \{ \begin{array}{ c } n \ k\end{array} \right \} x^{ \underline{ k } } = \sum_{ k = 0 }^n \sum_{ m = 0 }^k \left \{ \begin{array}{ c } n \ k\end{array} \right \} \left [ \begin{array}{ c } k \ m\end{array} \right ] ( - 1 )^{ n - k } x^m \\$.

由于这对任意$x$都成立,因此右边除了$x^n$以外的项系数均为$0$,而$x^n$的系数为$1$.前半部分是同理的.这个公式是斯特林反演的基础.

$\left \{ \begin{array}{ c } n + 1 \ m + 1\end{array} \right \} = \sum_{ k = m }^n \left ( \begin{array}{ c } n \ k\end{array} \right ) \left \{ \begin{array}{ c } k \ m\end{array} \right \} \\$.
$\left [ \begin{array}{ c } n + 1 \ m + 1\end{array} \right ] = \sum_{ k = m }^n \left ( \begin{array}{ c } n \ k\end{array} \right ) \left [ \begin{array}{ c } k \ m\end{array} \right ] \\$.

证明:对于前者,考虑组合意义,将$n + 1$个分为$m + 1$组,也就是先找一部分分成$m$组,再把剩下的分到一组.对于后者,也可以同样考虑组合意义.

补充斯特林恒等式

$\left \{ \begin{array}{ c } n \ m\end{array} \right \} = \sum_{ k = m }^n \left ( \begin{array}{ c } n \ k\end{array} \right ) \left \{ \begin{array}{ c } k + 1 \ m + 1\end{array} \right \} ( - 1 )^{ n - k } \\$.
$\left [ \begin{array}{ c } n \ m\end{array} \right ] = \sum_{ k = m }^n \left ( \begin{array}{ c } n \ k\end{array} \right ) \left [ \begin{array}{ c } k + 1 \ m + 1\end{array} \right ] ( - 1 )^{ n - k } \\$.

证明:由(5)(6),根据二项式反演可知.

$m ! \left \{ \begin{array}{ c } n \ m\end{array} \right \} = \sum_{ k = 0 }^m C_m^k k^n ( - 1 )^{ m - k } \\$.

证明:首先有$m^n = \sum_{ k = 0 }^m m^{ \underline{ k } } \left \{ \begin{array}{ c } m \ k\end{array} \right \} = \sum_{ k = 0 }^m k ! C_m^k \left \{ \begin{array}{ c } m \ k\end{array} \right \} \\$,对这个式子进行二项式反演即可.

$\left \{ \begin{array}{ c } n + 1 \ m + 1\end{array} \right \} = \sum_{ k = 0 }^n \left \{ \begin{array}{ c } k \ m\end{array} \right \} ( m + 1 )^{ n - k } \\$.

证明:

考虑组合意义,相当于先把前$k$个分为$m$组,把第$k + 1$个数放到第$m + 1$组.然后剩下$( n + 1 ) - ( k + 1 ) = n - k$个随便放.相当于我们按照每组所放的数的最小值区分每组.由于这么做,第$m + 1$组(最小值最大的那组)在$k$不同的时候最小值是不同的,因此一定不重不漏.

$\left [ \begin{array}{ c } n + 1 \ m + 1\end{array} \right ] = \sum_{ k = 0 }^n \left [ \begin{array}{ c } k \ m\end{array} \right ] C_{ n }^k ( n - k ) ! = n ! \sum_{ k = 0 }^n \frac{ \left [ \begin{array}{ c } k \ m\end{array} \right ] }{ k ! } \\$.

证明:

先考虑前半部分,首先如果$n > 0$,我们有$\left [ \begin{array}{ c } n \ 1\end{array} \right ] = ( n - 1 ) ! \\$.这个式子很显然,我们现在有一个长度为$n - 1$的环,想要往里插入第$n$个数有$n - 1$种选择,所以我们有:$\left [ \begin{array}{ c } n \ 1\end{array} \right ] = \left [ \begin{array}{ c } n - 1 \ 1\end{array} \right ] ( n - 1 ) \\$,数学归纳一下即可.

那么前半部分的组合意义就是:考虑将$n + 1$个数划分成$m + 1$个环,我们先将其中$k$个数划分成$m$个环,剩下$n + 1 - k$个数划分成另一个环.但是这样算显然会算重,所以我们只需要勒令第$n + 1$个数在最后一个环里即可.该证明就显然了.

而由于$C_n^k ( n - k ) ! = C_n^{ n - k } ( n - k ) ! = n^{ \underline{ n - k } } = \frac{ n ! }{ k ! } \\$.因此后半部分也得证.

$\left \{ \begin{array}{ c } n + m + 1 \ m\end{array} \right \} = \sum_{ k = 0 }^m k \left \{ \begin{array}{ c } n + k \ k\end{array} \right \} \\$.
$\left [ \begin{array}{ c } n + m + 1 \ m\end{array} \right ] \sum_{ k = 0 }^m ( n + k ) \left [ \begin{array}{ c } n + k \ k\end{array} \right ] \\$.

证明:

先考虑前者,我们将$n + k$个位置分到$k$个集合之后.还剩下$( n + m + 1 ) - ( n + k ) = ( m - k + 1 )$个数,剩下$( m - k )$个集合.

拿出来$( n + k + 1 )$这个数,剩下的数刚好够每个集合放一个.最后枚举一下把$( n + k + 1 )$放在哪里即可.由于每个划分一定存在一段(可能是$0$)单独自己集合的后缀.所以这个递推成立.后者也可以同样证明.

$C_n^m ( n - 1 )^{ \underline{ n - m } } = \sum_{ k = m }^n \left [ \begin{array}{ c } n \ k\end{array} \right ] \left \{ \begin{array}{ c } k \ m\end{array} \right \} \\$.

证明:

考虑$( n - 1 )^{ \underline{ n - m } } = \frac{ ( n - 1 ) ! }{ ( m - 1 ) ! } \\$,不妨设$f ( n , m ) = \sum_{ k = m }^n \left [ \begin{array}{ c } n \ k\end{array} \right ] \left \{ \begin{array}{ c } k \ m\end{array} \right \} \\$,相当于将$n$个数分成非空$m$组,然后组内的数要形成若干轮换的方案数.那么知道$f ( n , m ) = f ( n - 1 , m - 1 ) + ( n - 1 + m ) f ( n - 1 , m ) \\$.

设$g ( n , m ) = C_n^m \frac{ ( n - 1 ) ! }{ ( m - 1 ) ! } = \frac{ n ! ( n - 1 ) ! }{ m ! ( n - m ) ! ( m - 1 ) ! } \\$,那么知道:

$\begin{aligned} g ( n - 1 , m - 1 ) & = \frac{ ( n - 1 ) ! ( n - 2 ) ! }{ ( m - 1 ) ! ( n - m ) ! ( m - 2 ) ! } \\ g ( n - 1 , m ) & = \frac{ ( n - 1 ) ! ( n - 2 ) ! }{ m ! ( n - 1 - m ) ! ( m - 2 ) ! } \\ \end{aligned}$

显然$g ( n , m ) = g ( n - 1 , m - 1 ) + ( n - 1 + m ) g ( n - 1 , m ) \\$,数学归纳即可.

$C_n^m = \frac{ n ! }{ m ! ( n - m ) ! } = \sum_{ k = m }^n \left \{ \begin{array}{ c } n + 1 \ k + 1\end{array} \right \} \left [ \begin{array}{ c } k \ m\end{array} \right ] ( - 1 )^{ m - k } \\$.
$n^{ \underline{ n - m } } = \frac{ n ! }{ m ! } = \sum_{ k = m }^n \left [ \begin{array}{ c } n + 1 \ k + 1\end{array} \right ] \left \{ \begin{array}{ c } k \ m\end{array} \right \} ( - 1 )^{ m - k } ，其中 m \leq n \\$.

证明:考虑(5)(6),对其做一遍斯特林反演即可.

$\left \{ \begin{array}{ c } n \ l + m\end{array} \right \} C_{ l + m }^l = \sum_{ k = l }^n \left \{ \begin{array}{ c } k \ l\end{array} \right \} \left \{ \begin{array}{ c } n - k \ m\end{array} \right \} C_n^k \\$.
$\left [ \begin{array}{ c } n \ l + m\end{array} \right ] C_{ l + m }^l = \sum_{ k = l }^n \left [ \begin{array}{ c } k \ l\end{array} \right ] \left [ \begin{array}{ c } n - k \ m\end{array} \right ] C_n^k \\$.

证明:先考虑前者,左边即先将$n$个数分为$l + m$个集合,然后再挑出$l$个集合.那不妨枚举这$l$个集合中是哪些数,然后再进行分配.后者同理.

欧拉数

记$\left \langle \begin{array}\ n \ k\end{array} \right \rangle$表示$\{ 1 , 2 , . . . , n \}$的排列$a$中满足这条性质的排列个数:存在且只存在$k$个升高,换句话说,存在且只存在$k$个$i$,满足$1 \leq i < n$,$a_i < a_{ i + 1 }$.不难发现$\left \langle \begin{array}\ n \ k\end{array} \right \rangle = \left \langle \begin{array}\ n \ n - k - 1\end{array} \right \rangle$.

考虑在一个$\{ 1 , 2 , . . . , n - 1 \}$的排列中插入$n$,设插入的位置是原本$a_i$的后面,那么要么原本$a_i < a_{ i + 1 }$,要么反之.前者不会改变排列的升高的数量,后者则会增加$1$.另外还有一种情况是插入到了序列最前面.于是我们自然得到:$\left \langle \begin{array}\ n \ k\end{array} \right \rangle = ( k + 1 ) \left \langle \begin{array}\ n - 1 \ k\end{array} \right \rangle + ( n - k ) \left \langle \begin{array}\ n - 1 \ k - 1\end{array} \right \rangle$.

特别地,我们令$\left \langle \begin{array}\ 0 \ k\end{array} \right \rangle = [ k = 0 ]$,若$k < 0$,则$\left \langle \begin{array}\ n \ k\end{array} \right \rangle = 0$.

欧拉数与二项式系数

我们有Worpitzky恒等式:

$x^n = \sum_{ k \geq 0 } \binom{ x + k }{ n } \left \langle \begin{array} \\ n \\ k \end{array} \right \rangle , n \in \mathbb{ N }$

还有另一个恒等式:

$\left \langle \begin{array} \\ n \\ m \end{array} \right \rangle = \sum_{ k = 0 }^m \binom{ n + 1 }{ k } ( m + 1 - k )^n ( - 1 )^k$

剩下的不会了.

伯努利数

定义$B_j$为第$j$个伯努利数,且满足$\sum_{ j = 0 }^m \binom{ m + 1 }{ j } B_j = [ m = 0 ] , m \geq 0 \\$.

定义$S_m ( n ) = \sum_{ i = 0 }^{ n - 1 } i^m$.

伯努利数满足公式:$S_m ( n ) = \cfrac{ 1 }{ m + 1 } \sum_{ k = 0 }^m \binom{ m + 1 }{ k } B_k n^{ m + 1 - k } \\$.

证明如下:

对$S_{ m + 1 } ( n )$使用扰动法,我们有:

$\begin{aligned} S_{ m + 1 } ( n ) + n^{ m + 1 } & = \sum_{ k = 0 }^{ n - 1 } ( k + 1 )^{ m + 1 } \\ & = \sum_{ k = 0 }^{ n - 1 } \sum_{ j = 0 }^{ m + 1 } \binom{ m + 1 }{ j } k^j \\ & = \sum_{ j = 0 }^{ m + 1 } \binom{ m + 1 }{ j } S_j ( n ) \\ & = \sum_{ j = 0 }^{ m } \binom{ m + 1 }{ j } S_j ( n ) + S_{ m + 1 } ( n ) \\ n^{ m + 1 } & = \sum_{ j = 0 }^m \binom{ m + 1 }{ j } S_j ( n ) \\ \end{aligned}$

接下来使用数学归纳,假设$0 \leq j < m$时该公式成立,并假设有$S_m ( n ) = \cfrac{ 1 }{ m + 1 } \sum_{ k = 0 }^m \binom{ m + 1 }{ k } B_k n^{ m + 1 - k } + \Delta \\$,我们只需要证明$\Delta = 0$.

$\begin{aligned} n^{ m + 1 } & = \sum_{ j = 0 }^m \binom{ m + 1 }{ j } \cfrac{ 1 }{ j + 1 } \sum_{ k = 0 }^j \binom{ j + 1 }{ k } B_k n^{ j + 1 - k } + ( m + 1 ) \Delta \\ & = \sum_{ 0 \leq k \leq j \leq m } \binom{ j + 1 }{ k } \binom{ m + 1 }{ j } \cfrac{ 1 }{ j + 1 } B_k n^{ j + 1 - k } + ( m + 1 ) \Delta \\ & = \sum_{ 0 \leq k \leq j \leq m } \binom{ j + 1 }{ j - k } \binom{ m + 1 }{ j } \cfrac{ 1 }{ j + 1 } B_{ j - k } n^{ k + 1 } + ( m + 1 ) \Delta \\ & = \sum_{ 0 \leq k \leq j \leq m } \binom{ j + 1 }{ k + 1 } \binom{ m + 1 }{ j } \cfrac{ 1 }{ j + 1 } B_{ j - k } n^{ k + 1 } + ( m + 1 ) \Delta \\ & = \sum_{ 0 \leq k \leq m } \cfrac{ n^{ k + 1 } }{ k + 1 } \sum_{ j = k }^m B_{ j - k } \binom{ m + 1 }{ j } \binom{ j }{ k } + ( m + 1 ) \Delta \\ & = \sum_{ 0 \leq k \leq m } \cfrac{ n^{ k + 1 } }{ k + 1 } \binom{ m + 1 }{ k } \sum_{ j = k }^m B_{ j - k } \binom{ m + 1 - k }{ j - k } + ( m + 1 ) \Delta \\ & = \sum_{ k = 0 }^m \cfrac{ n^{ k + 1 } }{ k + 1 } \binom{ m + 1 }{ k } \sum_{ j = 0 }^{ m - k } B_{ j } \binom{ m + 1 - k }{ j } + ( m + 1 ) \Delta \\ & = \sum_{ k = 0 }^m \cfrac{ n^{ k + 1 } }{ k + 1 } \binom{ m + 1 }{ k } [ m - k = 0 ] + ( m + 1 ) \Delta \\ & = n^{ m + 1 } + ( m + 1 ) \Delta \end{aligned}$

显然$\Delta = 0$,上式成立.

斐波那契数

定义斐波那契数$F_n = \begin{cases}0 & n = 0 \ 1 & n = 1 \ F_{ n - 1 } + F_{ n - 2 } & n > 1\end{cases}$.

斐波那契数的扩展定义

首先根据数学归纳,不难证明卡西尼恒等式:

$F_{ n + 1 } F_{ n - 1 } - F_n^2 = ( - 1 )^n , n > 0$

事实上,如果我们将斐波那契数的递推式改写作:$F_n = F_{ n + 2 } - F_{ n + 1 }$,我们可以在$n \in \mathbb{ Z }$的时候定义斐波那契数,同样也是满足上面的恒等式的,而且我们可以发现:

$F_{ - n } = ( - 1 )^{ n - 1 } F_n , n \in \mathbb{ Z }$

斐波那契数与数论

如果我们考虑不断使用斐波那契递推式展开,不难发现:

$\begin{aligned} F_{ n + k } & = F_k F_{ n + 1 } + F_{ k - 1 } F_n \\ F_{ n + m + 1 } & = F_{ n + 1 } F_{ m + 1 } + F_n F_m \end{aligned}$

另外,如果我们在上面这个式子中取$k = wn , w \in \mathbb{ N }$并使用归纳法,我们又可以得到一个性质:$F_{ kn }$是$F_n$的倍数,$k \in \mathbb{ Z }$.

再观察这个式子,使用归纳法可以证明$\gcd ( F_{ n } , F_{ n - 1 } ) = 1$,进一步有:$\gcd ( F_{ n + m } , F_m ) = \gcd ( F_n , F_m )$.

如果我们推广这个结论,就可以得到一个重要的性质:

$\gcd ( F_m , F_n ) = F_{ \gcd ( n , m ) }$

如果我们再一次推广这个结论,可以得到马蒂亚舍维奇引理:

$F_n^2 | F_m \Leftrightarrow nF_n | m , n > 2$

这个引理的证明如下:

由于$F_{ n + 1 } \equiv F_{ n - 1 } \pmod{ F_n }$.于是我们有:$F_{ 2 n } = F_n F_{ n + 1 } + F_{ n - 1 } F_n$,也就是$F_{ 2 n } \equiv 2 F_n F_{ n + 1 } \pmod{ F_n^2 }$.

另外我们有:$F_{ 2 n + 1 } \equiv F_{ n + 1 }^2 \pmod{ F_n^2 }$.

同理,使用归纳法可以证明:$F_{ kn } \equiv kF_n F_{ n + 1 }^{ k - 1 } \pmod{ F_n^2 } , F_{ kn + 1 } \equiv F_{ n + 1 }^k \pmod{ F_n^2 }$.

而$F_{ n + 1 } \bot F_n$,于是$F_{ kn } \equiv 0 \pmod{ F_n^2 } \Leftrightarrow k \equiv 0 \pmod{ F_n } , n > 2$.

斐波那契数系

我们如果定义$j \gg k \Leftrightarrow j \geq k + 2$,那么有齐肯多夫定理:

每个正整数都有唯一的表示方式满足:$n = \sum_{ i = 1 }^r F_{ k_i } , \forall 1 \leq i < r , k_i \gg k_{ i + 1 } \gg 0$.

首先证明存在性:我们考虑数学归纳,对于一个数n,如果$\exists k$满足$F_k = n$,则显然成立,不然,应$\exists k$满足$F_k < n < F_{ k + 1 }$,而$n - F_k$的表示已经存在了.另外,由于$n - F_k < F_{ k + 1 } - F_k = F_{ k - 1 }$,因此必定不可能出现选了$F_k$又选了$F_{ k - 1 }$的情况,存在性得证.

至于唯一性,如果我们不选择$F_k$而是选择$F_{ k - 1 }$,那么显然接下来无论怎么选,它们的加和都不可能大于等于$F_k$,因此一定是唯一的.

这样的话,我们可以将一个自然数$n$以斐波那契数的形式表示出来.

斐波那契数的封闭形式

使用生成函数,令$F ( z ) = \sum_{ k \geq 0 } F_k z^k$.那么不难发现$F ( z ) - zF ( z ) - z^2 F ( z ) = z$,也就是$F ( z ) = \cfrac{ z }{ 1 - z - z^2 }$.

考虑这个形式一定可以分解为$F ( z ) = \cfrac{ a }{ 1 - \alpha z } + \cfrac{ b }{ 1 - \beta z }$的形式,而这两种形式对应的生成函数都很显然.

进行因式分解,如果令$\phi = \cfrac{ 1 + \sqrt{ 5 } }{ 2 } , \hat \phi = \cfrac{ 1 - \sqrt{ 5 } }{ 2 }$,那么可以得到$F_n = \cfrac{ 1 }{ \sqrt{ 5 } } ( \phi^n - \hat \phi^n )$.

另外,由于$\hat \phi^n$的影响很小,于是又有$F_n = \lfloor \cfrac{ \phi^n }{ \sqrt{ 5 } } + 0 . 5 \rfloor$.

连项式

连项式多项式$K_n ( x_1 , x_2 , . . . , x_n )$定义为:$K_n ( x_1 , x_2 , . . . , x_n ) = \begin{cases}1 & n = 0 \ x_1 & n = 1 \ x_n K_{ n - 1 } ( x_1 , x_2 , . . . x_{ n - 1 } ) + K_{ n - 2 } ( x_1 , x_2 , . . . , x_{ n - 2 } ) & n \geq 2\end{cases}$.

通过定义不难发现:$K_n ( 1 , 1 , . . . , 1 ) = F_{ n + 1 }$.

继续观察式子,会发现它递归的过程相当于枚举是否消掉相邻的一对数$( x_{ n - 1 } , x_n )$.我们考虑用这样一种形式的字符串来表示最后某一项的情况:’.’为还没有消除掉的项,长度为$1$;’-‘为已经消除了的两项,长度为$2$.那么$K_n ( x_1 , x_2 , . . . , x_n )$就可以表示为一个长度为$n$的字符串,其中若有$k$个’-‘,有$n - 2 k$个’.’,则有$\binom{ n - k }{ k }$种不同的排列方式.

于是我们有:

$\begin{aligned} K_n ( z , z , . . . , z ) & = \sum_{ k = 0 }^n \binom{ n - k }{ k } z^{ n - 2 k } \\ \end{aligned}$

另外,这也导出:$F_{ n + 1 } = \sum_{ k = 0 }^n \binom{ n - k }{ k } \\$.

考虑上面的构造过程,不难发现$K_n ( x_1 , x_2 , . . . , x_n ) = K_n ( x_n , x_{ n - 1 } , . . . , x_1 )$.

于是递归式可以写成:$K_n ( x_1 , x_2 , . . . , x_n ) = x_1 K_{ n - 1 } ( x_2 , x_3 , . . . x_{ n } ) + K_{ n - 2 } ( x_3 , x_4 , . . . , x_{ n } )$.

进一步地,不断展开后得到:

$\begin{aligned} K_{ m + n } ( x_1 , . . . , x_m , x_{ m + 1 } , . . . , x_{ n + m } ) & = \\ K_m ( x_1 , . . . , x_m ) K_n ( x_{ m + 1 } , . . . , x_{ n + m } ) + K_{ m - 1 } ( x_1 , . . . , x_{ m - 1 } ) K_{ n - 1 } ( x_{ m + 2 } , . . . , x_{ n + m } ) \end{aligned}$

另外,根据连项式的定义,不难导出$K_n ( x_1 , . . . , x_n + y ) = K_n ( x_1 , . . . , x_n ) + K_{ n - 1 } ( x_1 , . . . , x_{ n - 1 } ) y$.

由这个公式可以推出:$\cfrac{ K_{ n + 1 } ( a_0 , . . . , a_n ) }{ K_n ( a_1 , . . . , a_n ) } = \cfrac{ K_n ( a_0 , . . . , a_{ n - 1 } + \cfrac{ 1 }{ a_n } ) }{ K_{ n - 1 } ( a_1 , . . . , a_{ n - 1 } + \cfrac{ 1 }{ a_n } ) }$.

不断做这个迭代,于是我们可以得到连项式与连分数之间的关系:

$\cfrac{ K_{ n + 1 } ( a_0 , . . . , a_n ) }{ K_n ( a_1 , . . . , a_n ) } = a_0 + \cfrac{ 1 }{ a_1 + \cfrac{ 1 }{ a_2 + \cfrac{ 1 }{ a_3 + . . . } } }$

另外,这个与数论中的Stern-Brocot树有很大关系,暂略.

简单乐理

发表于 2025-06-23 分类于大学课程 Waline：

前言

这个博客是北京大学课程《音乐与数学》的相关笔记.然而我懒得画五线谱以及插入钢琴图片,所以这里我们只空谈理论.

本人在大学前并未学过相关乐理,所以下面的个人理解当然可能会出错.

泛音列

拍音理论

假设两个正弦单音的频率分别是$\omega , \omega + \delta$,那么它们叠加后是:

$\begin{aligned} & \sin ( 2 \pi ( \omega + \delta ) t ) + \sin ( 2 \pi \omega t ) \\ = & 2 \sin \left ( 2 \pi ( \omega + \frac{ \delta }{ 2 } ) t \right ) \cos ( \pi \delta t ) \end{aligned}$

注意到这个声音受到$\cos ( \pi \delta t )$的控制.因此会以$\frac{ \delta }{ 2 }$的频率振动,由于$\delta$应该远小于$\omega$,这里就会产生$\delta = | \omega_1 - \omega_2 |$个拍音.

Mersenne定律

考虑弦乐的情况,将一根弦理想化后,可以只关注它的三个参数:

弦长$L$.
张力$T$.
线密度$\rho$.

对于弦的振动解微分方程,这里我不是很想解了啊!所以我们直接放结论,对于弦上一个点$u ( x , t )$,首先是一维振动方程:

$\frac{ \partial^2 u }{ \partial x^2 } = \frac{ \rho }{ T } \frac{ \partial^2 u }{ \partial t^2 }$

最终得到的会是一个无穷级数,这个无穷级数的每一项都形如:

$u_n ( x , t ) = c_n \sin ( \omega_n t + \theta_n ) \sin ( \frac{ n \pi }{ L } x )$

其中第$n$项的频率满足:

$f_n = \frac{ n }{ 2 L } \sqrt{ \frac{ T }{ \rho } }$

其中我们将$f_1$称为基频,相应的声音称为基音,而将剩下的频率对应的声音统称为泛音,其中$f_n , n \geq 2$对应的是第$n - 1$泛音.

特别地,如果我们干脆记$f = f_1$,上述结果告诉我们弦的振动产生的一列频率是:

$f , 2 f , 3 f , \cdots$

这个序列通常被称为泛音列.

特别地,上述的频率其实是固定了点来讨论的,实际上的泛音要更为复杂,会在一根弦上的不同位置处产生不同的加权.实际上对于不同的$n$,它们的泛音列长这个样子: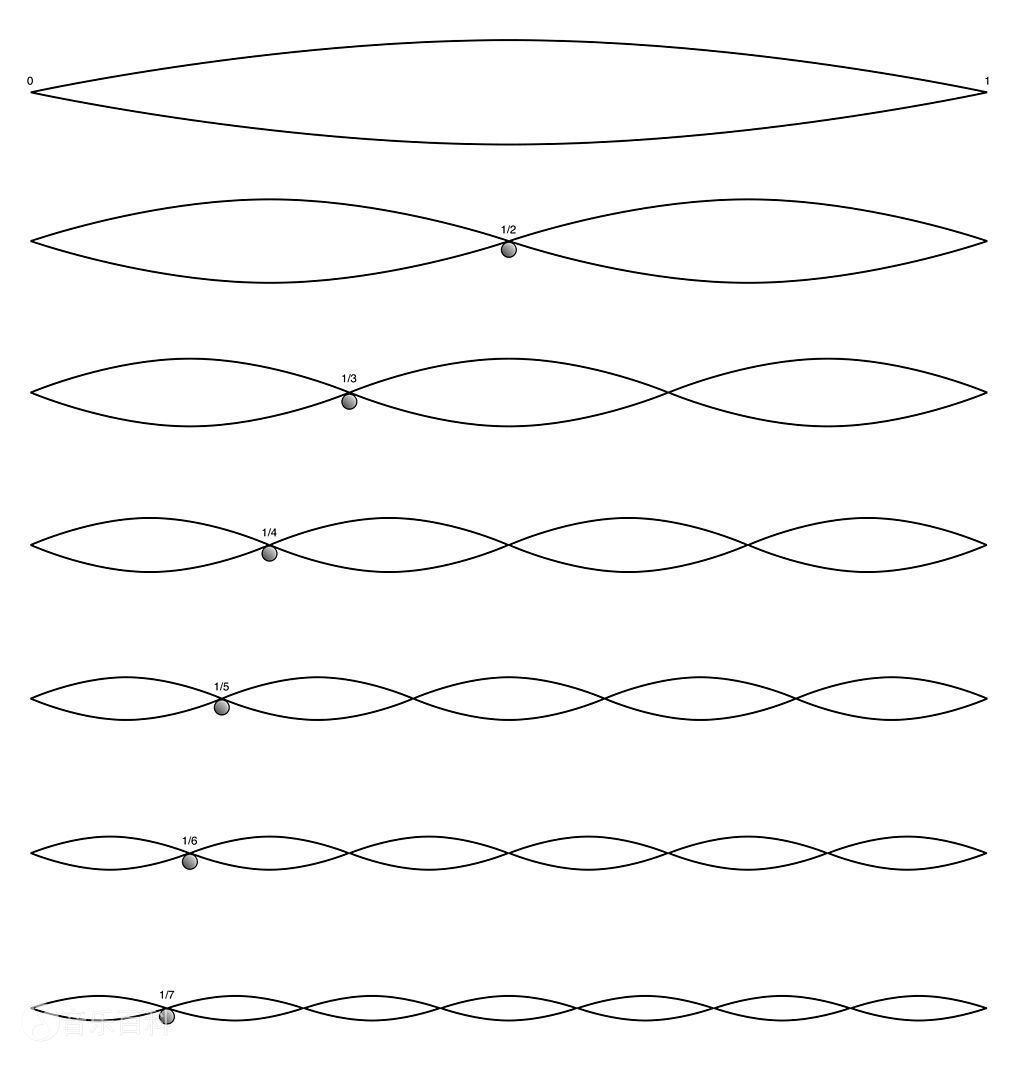

其中标注的点(波节)在振动中均是固定不变的.

这其实是某些弦乐演奏中一些按弦技巧的基础.例如这里,如果我用手轻触中间点,我就可以消灭掉所有的$f_{ 2 k + 1 }$,泛音列中只剩下$2 f , 4 f , \cdots$.我们后面会再提这个事,这意味着我弹出的音高了八度.那如果我按$\frac{ 1 }{ 3 }$处呢?那泛音列中就会只剩下$3 f , 6 f , 9 f , \cdots$,也就是先高一个纯八度,再高一个纯五度.

还有拨弦,如果我在中间拨弦会发生什么呢?由于我的拨动使得整个弦应该以中间为对称形成一个偶函数,中间的点一定在波动,因此泛音列中剩下的就会是$f , 3 f , 5 f , \cdots$.

管乐器

管乐器中振动的变为空气柱,不过吧空气柱这个东西振动的时候会略微超出管口,因此会有管口矫正这个事存在.

再就是,管乐器其实分为两种:开管(两面开口)和闭管(单面开口).而且不像琴弦的两端是固定的.一个自然的想法是,根据上面我们放的那张图,开口的那个位置一定要振动,而闭口的那个位置一定被卡住不动.这意味着开管和闭管的泛音列天然不同.具体来说:

开管的泛音列:

$f , 2 f , 3 f , 4 f , \cdots$

闭管的泛音列:

$f , 3 f , 5 f , 7 f$

另外,相同长度的管,开管的基音比闭管高了一个八度.

管乐器有一种演奏方式是超吹.简单来说,当你用力吹的时候,直觉上随着你用力越大,你吹出来的音的频率应该是连续的.但实际上听感更接近于离散的.这是因为从一开始整个泛音列就都是存在的,只是当气流加快的时候,后面的音在某种程度上被”加强”了,所以对于开管来说,你会先听到一个高八度的音,再听到一个高五度的音.

泛音列重合理论

既然如此,我们可以见到,当两个音的基频的比较为简单的时候,它们产生的泛音列重合程度就会较高.例如:

$\begin{gathered} f , 2 f , 3 f , 4 f , \cdots \\ 2 f , 4 f , 6 f , 8 f , \cdots \end{gathered}$

或是:

$\begin{gathered} f , 2 f , 3 f , 4 f , \cdots \\ \frac{ 3 }{ 2 } f , 3 f , \frac{ 9 }{ 2 } f , 6 f , \cdots \end{gathered}$

这从相当的程度解释了为什么理想的音程全都是简单整数比.

律制

要讲律制,首先要知道从经验上来讲,人耳对于音乐的听觉其实并非线性.换言之,当你听两个音的时候,你关注的可不是它们之间的频率差值,而可能更关注它们之间的频率比值.类似地,其实人听声压的时候靠的也是比值,例如分贝的定义是$L_p = 20 \log_{ 10 } ( \frac{ p }{ p_0 } )$,其中$p_0 = 20 \mu Pa$.

音程

我们称两个音级之间的距离为音程,其中高的音称为冠音,而低的音被称为根音,一个音程应该由两个参数决定:度数和半音数,简单来说,度数是跨越的音名数量,而半音数是跨越的半音数量.表格长这样:

| 度数 | 半音数 | 名称 |

| —— | ——— | ——— |

| 一 | 0 | 纯一度 |

| 二 | 1 | 小二度 |

| 二 | 2 | 大二度 |

| 三 | 3 | 小三度 |

| 三 | 4 | 大三度 |

| 四 | 5 | 纯四度 |

| 四 | 6 | 增四度 |

| 五 | 6 | 减五度 |

| 五 | 7 | 纯五度 |

| 六 | 8 | 小六度 |

| 六 | 9 | 大六度 |

| 七 | 10 | 小七度 |

| 七 | 11 | 大七度 |

| 八 | 12 | 纯八度 |

从这套理论出发,毕达哥拉斯说我们找一下最简整数比:注意到:

| 音程 | 频率比 |

| ——— | ——— |

| 纯八度 | $2 : 1$ |

| 纯五度 | $3 : 2$ |

| 纯四度 | $4 : 3$ |

| 大三度 | $5 : 4$ |

| 小三度 | $6 : 5$ |

看上去太漂亮了对吧!但是就是这个规定出了大锅.

五度相生律

中国的三分损益法和毕达哥拉斯的五度相生法其实是类似的东西,我们这里只考虑五度相生律.

毕达哥拉斯学派说,我们这么干,规定$C$的频率(当时其实不存在频率的概念,但我们这里就为了方便这么说了)为$1$,然后每次向上升一个纯五度,如果超出去了呢,那就降一个八度降回来.回忆到纯五度是七个半音,这相当于求$\{ 7 k \} \pmod{ 12 }$这个数列对吧,简单数论知识告诉我们它必然能遍历$12$种情况,具体而言:

$\begin{aligned} C \to & & G \to & & D \to & & A \to & & E \to & & B \to \\ 1 \to & & \frac{ 3 }{ 2 } \to & & \frac{ 3^2 }{ 2^3 } \to & & \frac{ 3^3 }{ 2^4 } \to & & \frac{ 3^4 }{ 2^6 } \to & & \frac{ 3^5 }{ 2^7 } \to \\ \\ \\ \# F \to & & \# C \to & & \# G \to & & \# D \to & & \# A \to & & \# E \\ \frac{ 3^6 }{ 2^9 } \to & & \frac{ 3^7 }{ 2^{ 11 } } \to & & \frac{ 3^8 }{ 2^{ 12 } } \to & & \frac{ 3^9 }{ 2^{ 14 } } \to & & \frac{ 3^{ 10 } }{ 2^{ 15 } } \to & & \frac{ 3^{ 11 } }{ 2^{ 17 } } \\ \end{aligned}$

我们是拿纯八度和纯五度生成的所有的音,因此纯五度肯定是准的,那么与之对应的纯四度肯定是准的.但是看三度音程就会发现问题,例如大三度$CE$的比是$\frac{ 81 }{ 64 } > \frac{ 80 }{ 64 } = \frac{ 5 }{ 4 }$.

更难过的是就算我们按照纯八度和纯五度生成的,这个纯八度也有点难绷.具体而言这里的$# E \ne F$,你对着这个$# E$往上再升一个音得到的理应是$C ‘ = \frac{ 3^{ 12 } }{ 2^{ 18 } } > 2$,具体来说$\frac{ 3^{ 12 } }{ 2^{ 19 } } \approx 1 . 013643$,这就出事了,这个东西转一圈并没有转到理想的纯八度音阶上,这个问题在中国古代的三分损益上也体现了,那里的名字叫旋宫不归,这里的话则是将这个略大于$1$的数叫做毕达哥拉斯音差.

仔细分析一下就会发现这个问题几乎是不可避免的,因为你上升$12$个纯五度,再下降$7$个纯八度理应回到原点,可是:

$( \frac{ 3 }{ 2 } )^{ 12 } \times ( \frac{ 1 }{ 2 } )^7 > 1$

这下这下了.

纯律

其实我们刚才就能见到真正完美符合简单整数比的律根本调不出来.但是能不能让一些常用的音程(比如纯八度,纯五度,纯四度,大三度)尽可能准呢.这就是纯律在干的事.

还是规定$C$的频率为$1$.接下来用正三和弦(一个大三度和一个小三度)$I : C - E - G$,$IV : F - A - C ‘$,$V : G - B - D ‘$的比例是$4 : 5 : 6$确定剩下的:

$\begin{aligned} C & & D & & E & & F & & G & & A & & B & & C ' & & D ' \\ 1 & & \frac{ 9 }{ 8 } & & \frac{ 5 }{ 4 } & & \frac{ 4 }{ 3 } & & \frac{ 3 }{ 2 } & & \frac{ 5 }{ 3 } & & \frac{ 15 }{ 8 } & & 2 & & \frac{ 9 }{ 4 } \end{aligned}$

所以现在大三度和小三度都准了.但问题又来了:

五度音程$D - A$不协和,比例为$\frac{ 80 }{ 54 } < \frac{ 81 }{ 54 } = \frac{ 3 }{ 2 }$.这直接导致了转调会出错.
有两种不同的大二度:音程$C - D , F - G , A - B$的比例是$\frac{ 9 }{ 8 }$而音程$D - E , G - A$的比例为$\frac{ 10 }{ 9 }$.
谐调音差:从$C$出发升高四个纯五度,降低两个八度和一个大三度后,得到的是:$( \frac{ 3 }{ 2 } )^4 \times ( \frac{ 1 }{ 2 } )^2 \times \frac{ 4 }{ 5 } = \frac{ 81 }{ 80 } = 1 . 0125 > 1$.

十二平均律

既然我们一开始就说了律是根据比值来定的,为什么不直接简单一点,干脆用$\sqrt[12]{ 2 }$来平均律制呢?于是将近五百年前就有了朱载堉这位手开十二次根号的神人.这也是所有律法中几乎最简单的一种了,以至于我到这里发现没啥可写的了.

但它的问题也是最一眼能看出来的,那就是除了纯八度,全都不准.

先在这里定义音分的概念,设两个声音的频率分别是$f_1 , f_2$,则它们的音分数定义为$1200 \log_2 ( \frac{ f_2 }{ f_1 } )$,容易见到十二平均律拿到的一个半音恰好是$100$音分.

用音分可以迅速确定一下,发现十二平均律这玩意准的离谱,虽然哪里都差一点,但哪里差的都不多.

调式

大小调

自然大调

就是我们最常用的$CDEFGABC ‘$,用大二度和小二度组织调式.具体而言,以一个大二度分开了两组四声音阶(均为大大小),按顺序分别为:

主音
上主音
中音
下属音
属音
下中音
导音

用五度相生,下属音$\rightarrow$主音$\rightarrow$属音.

自然小调

以一个大二度分开了两组四声音阶(分别为大小大和小大大)

以$ABCDEFG$用的调子,然而这里的问题是$G$作为导音却和$A ‘$差了个全音,导得不好.

和声小调

以一个大二度分开了两组四声音阶(分别为大小大和小增小)

将自然小调的导音升高一个半音.用$A , B , C , D , E , F , (^# G )$.

但是这样出了个增二度.

旋律小调

以一个大二度分开了两组四声音阶(分别为大小大和大大小)

把下中音也升上去,这样差的就小,用$A , B , C , D , E , (^# F ) , (^# G )$.

可以见到小调改音的主要目的是为了调导音的作用,这种作用只有在上行音阶的时候才是需要人为更改的,因此下行音阶不改音,与自然小调的下行音阶保持一致.

升降号调

以五度相生:

$C \to G \to D \to A \to E \to B \to (^\# F ) \to (^\# C )$

依次考虑它们为主调的自然大调音阶.

大调音阶的前后是对称的全全半+全+全全半结构,跳一个五度刚好能从前半部分跳到后半部分,因此从$C$开始每次往后跳一次都要在一个音阶上增一个升号.从$C$大调提升到$G$大调的时候就是将$C$的下属音(也就是$F$)升音.

对称地,反方向的五度相生:

$C \to F \to (^b B ) \to (^b E ) \to (^b A ) \to (^b D ) \to (^b G ) \to (^b C )$

那这个应该降什么呢?比如从$C$大调提升到$F$大调的时候就是将$F$的下属音$B$降一个音对吧.

所以最后的结果就是:

一个自然大调将主音向前挪小三度就得到了一个自然小调,它们称为一对关系大小调.

具有相同主音的大小调被称为平行大小调.其实也就是名字精确到大小写是一样的.

一个大调的下属音大调和属音大调以及对应的关系小调称为其近关系调.

和弦

三和弦

按照三度音程叠起来的三个音所构成的和弦被称为三和弦.其中最下面的音被称为根音,最上面的音被称为冠音或者五音,中间的被称为三音.

由于三度音程分大小,所以就有了四种不同的三和弦.

大三和弦:下面一个大三度,上面一个小三度,刚好形成$4 : 5 : 6$的频率关系.
小三和弦:下面一个小三度,上面一个大三度.
减三和弦:两个小三度.
增三和弦:两个大三度.

七和弦

按照三度音程叠四个音构成的和弦被称为七和弦.除去其中由三个大三度构成的(这样使得最上方的七音和最底下的根音形成了八度)以外,其余七种七和弦依照三和弦名称+七度音阶名称的原则命名,如下:

减减七和弦(减七和弦):小小小.
减小七和弦(半减七和弦):小小大.
小小七和弦(小七和弦):小大小.
小大七和弦:小大大.
大小七和弦(属七和弦):大小小.
大大七和弦(大七和弦):大小大.
增大七和弦:大大小.

很遗憾的是七和弦全部包含至少一个不协和音程,所以它们全都是不协和和弦.

和弦转位

以根音为低音的和弦为原位和弦,以三五七音为低音的则称为转位和弦.

对于三和弦来说:

以三音作为低音的称为第一转位,也称作六和弦.
以五音作为低音的称为第二转位,也称作四六和弦.

对于七和弦来说:

以三音作为低音的称为第一转位,也称作五六和弦.
以五音作为低音的称为第二转位,也称作三四和弦.
以七音作为低音的称为第三转位,也称作二和弦.

和弦的调性

在调式的主音,下属音,属音上的和弦分别被称为主和弦(I),下属和弦(IV),属和弦(V),它们被统称为正和弦,在C大调中体现为$C - E - G$,$F - A - C ‘$,$G - B - D ‘$.其中主和弦一般比较稳定,属和弦则比较飘渺,下属和弦往往则起到过度作用.

一定范围内的和弦连接被称为和声进行,下面是三种基本形式:

正格进行:$I \to V \to I$.
变格进行:$I \to IV \to I$.
复式进行:$I \to IV \to V \to I$.

对于大调来说,其不同的三和弦之间有更加复杂的关系.经验给出以下图表:

$\xymatrix{ & & & & I \\ & & IV \ar[r] \ar[d] \ar[dr] \ar[rru] & vii \degree \ar[ru] & \\ iii \ar[r] & vi \ar[r] \ar[ru] & ii \ar[r] \ar[ru] & V \ar[ruu] & }$

其中$I$较为特殊,可以走向全部的和弦,这里略去不画.

新黎曼理论

引入以下三种对三和弦的变换(均会使得大和弦变小和弦,小和弦变大和弦):

平行变换$P$:保持纯五度音阶不变,将三音切换.
关系变换$R$:保持大三度音阶不变,补上剩下的一个(等价于大小调转换).
导音变换$L$:保持小三度音阶不变,补上剩下的一个.

容易见到$R \circ ( L \circ R )^3 = P$.

随机算法

发表于 2025-06-23 更新于 2025-09-26 分类于大学课程 Waline：

随机化算法

基本分析

Union Bound

即:$Pr [ \bigcup_i X_i ] \leq \sum Pr [ X_i ]$,取等当且仅当所有$X_i$互斥.

Markov 不等式

若$X \geq 0$,则$Pr [ X \geq t \mathbb{ E } [ X ] ] \leq \frac{ 1 }{ t }$.

Example(Max-Cut算法)

一个无向无权图,将点集划分成两个部分,使得跨越这两部分的边尽可能多.

直接随机划分,容易见到每条边有$\frac{ 1 }{ 2 }$的概率是割边,因此期望自然是$\frac{ 1 }{ 2 } | E | \geq \frac{ 1 }{ 2 } | \text{ max - cut } |$.

由此立即见到,$Pr [ | ans | \leq ( \frac{ 1 }{ 2 } - \epsilon ) | E | ] = Pr [ | E | - | ans | \geq ( \frac{ 1 }{ 2 } + \epsilon ) | E | ] \leq \frac{ 1 }{ 1 + 2 \epsilon }$.

由于每次独立操作,因此如果有$P$的概率失败,那么运行$T$次后至少成功一次的概率应当为$1 - P^T$.从而$T = O ( \log_P{ \delta } ) = O ( \cfrac{ \ln \frac{ 1 }{ \delta } }{ \ln ( 1 +{ 2 \epsilon } ) } ) \approx O ( \cfrac{ \ln \frac{ 1 }{ \delta } }{ \epsilon } )$即可拿到$\delta$失败概率.

Chernoff Bound

设$X_1 , \cdots , X_n \in [ 0 , 1 ]$是独立,同期望(期望为$\mu \geq t$)的随机变量,令$X = \frac{ \sum_k X_k }{ n }$,对于任何失败概率$\delta \in ( 0 , 1 )$,应当有:

$Pr \left [ | X - \mu | \geq \sqrt{ \cfrac{ \log ( 1 / \delta ) }{ nt } } \mu \right ] \leq \delta$

Example(Median Trick)

现在有一个黑盒能够以$p > \frac{ 1 }{ 2 }$的概率正确回答Yes或者No,问重复$T$选多少次能拿到$1 - \delta$的成功概率.

考虑重复$T$次后应当有期望$pT$个正确答案,因此直接取中位数.称此算法为Median Trick.

Chernoff Bound 告诉我们$T = O ( \log \frac{ 1 }{ \delta } )$足够.

Hoeffding 不等式

设独立随机变量$x_1 , \cdots , x_m \in [ s , t ]$,令$X = \sum_i x_i$,则:

$Pr [ X - E [ X ] \geq z ] \leq 2 \exp \left ( - \cfrac{ 2 z^2 }{ m ( t - s )^2 } \right )$

编程中的随机性

一般采用伪随机,也即是给定初值$X_0$,通过某个确定性的函数来生成$X_{ n + 1 } = f ( X_n )$这样的.

数值概率算法

即通过随机选取元素从而求得在数值上的近似解.较之于传统算法,其运行速度更快,而且随着运行时间的增加,近似解的精度也会提高.在不可能或不必要求出问题的精确解时,可以使用其得到相当满意的近似解,如随机撒点法(近似求难以计算的图形面积).

Monte Carlo算法

总是能在确定的运行时间内出解,但是得到的解有一定概率是错的.通常出错的概率比较小,因此可以通过反复运行算法来得到可以接受的正确率.

求解最优化问题的Monte Carlo算法

事实上,大部分最优化问题都可以转化为判定性问题:也就是判定一个解是否是最优解,因此我们接下来基本都是讨论的求解判定性问题的Monte Carlo算法.

求解判定性问题的Monte Carlo算法

假倾向的Monte Carlo算法:当这类算法的返回值为假的时候,结果一定正确,但返回值为真的时候则有一定概率错误.
真倾向的Monte Carlo算法:当这类算法的返回值为真的时候,结果一定正确,但返回值为假的时候则有一定概率错误.
产生双侧错误的Monte Carlo算法:无论返回值为什么都有概率出错.基本不会使用.

以下讨论的Monte Carlo算法均为产生单侧错误的Monte Carlo算法.

正确率与复杂度

显然,如果我们有一个单词正确率为$p$,时间复杂度为$O ( f ( n ) )$的算法,我们运行其$k$次,则正确率为$1 - ( 1 - p )^k$,时间复杂度为$O ( kf ( n ) )$.

算法设计思路1

我们来总结一下通常的Monte Carlo算法的设计思路:

设计一个能解决问题的确定性算法

这个算法需要枚举一些元素.
设这个算法的复杂度为$O ( f ( n ) g ( n ) )$,其中$f ( n )$为枚举部分的复杂度,$g ( n )$为单词枚举中计算所需的复杂度.大部分情况下应保证$g ( n )$不会很大.

向算法引入随机化优化复杂度

随机化寻找元素来降低复杂度.
计算随机化情况下的正确率以及复杂度.

算法设计思路2

设计一个能解决问题的确定性算法

这个算法需要用到一个或多个传入的元素.
这个元素的值不应该依赖于输入数据.
我们可以通过check这个元素来得到与答案有关的信息.

向算法引入随机化优化复杂度

随机这个元素.
计算随机化情况下的正确率以及复杂度

Example

Example 1(Millar-Rabin算法)

略

Example2(CodeChef MSTONE)

平面上有$n$个互不重合的点,已知存在不超过$7$条直线可以覆盖全部的点,问在平面上作一条直线,最多能覆盖多少个点.$n \leq 10000$.

考虑一个朴素的暴力:枚举两个点,确定一条直线,然后判断多少个点在这条直线上.但是这样复杂度是$O ( n^3 )$的.

考虑加入随机化.我们不妨每次随机两个点,注意到存在七条直线覆盖全部的点,那覆盖点最多的直线覆盖的点数一定不少于$\lceil \frac{ n }{ 7 } \rceil$个点.换句话说,我们随机一个点,这个点在这条直线上的概率是$\frac{ 1 }{ 7 }$,因此随机两个点确定这条直线的概率为$\frac{ 1 }{ 49 }$.随机$1000$次,错误概率为$1 - ( \frac{ 48 }{ 49 } )^{ 1000 }$,是很小的.

Example3(CF364D Ghd)

给定一个长度为$n$的序列,要求找出一个长度大于等于$\frac{ n }{ 2 }$的子序列,使这个子序列中所有数的$\gcd$最大,求最大的$\gcd$.$n \leq 10^6$,$a_i \leq 10^{ 12 }$.

注意到我们随机一个数,这个数在最终答案中的概率是$\frac{ 1 }{ 2 }$.我们不妨直接随机这个数,然后枚举它的因子,判断每个因子在序列中的出现次数即可.但是这样单次复杂度$O ( n \sqrt{ a } )$,好像不太能过.

冷静一下,我们不妨将这$\sqrt{ a }$个质因子全都存下来,然后将$n$个数也全都存下来,做狄利克雷后缀和即可.不过直接做可能还需要离散化/map,我们考虑先把所有数与我们随机到的那个数取一个$\gcd$,这样所有数就都是这个数的因子,可以使用大小因子分别编号来实现.

Example4([POI2014]Couriers)

给定长度为$n$的序列$a$,有$m$次询问,每次给定一个区间$[ l , r ]$,问$a [ l , r ]$中是否存在出现次数严格大于其它所有数出现次数之和的数,如果存在请输出.$( n , m \leq 500000 , 1 \leq a_i \leq n )$.

先存下来每个位置的数是第几次出现,我们就可以利用二分快速找到一个区间内某个数出现次数.接下来只需要随机化找这个区间内某个数并判断是否满足条件即可.

Example5([NOI2013] 向量内积)

先考虑$k = 2$的情况:

首先,我们自然可以枚举一个向量$A$并判断它与其它向量的内积,这样复杂度为$O ( n^2 d )$.

冷静一下,这个过程其实就是一个矩阵乘法的过程:我们设$A = \begin{bmatrix}\vec{ a_1 } , \vec{ a_2 } , . . . , \vec{ a_n }\end{bmatrix}$,那我们要验证的无非是$B = AA^T$中是否存在一个不在主对角线上的元素$B_{ i , j }$在$\mod 2$意义下为$0$.

这咋做啊?我们冷静一下,构造一个矩阵$C$,其中$C$的主对角线元素与$B$相同,而其他元素全是$1$.接下来我们要做的无非是找到$B$和$C$不同的地方.

这咋办呢?我们考虑这么一点:如果$B = C$,那么对于任意一个$X_{ m \times n }$都应该满足$XB = XC$,取$m = 1$,我们的问题就转化为:是否能找到一个$X$,使得$XB \ne XC$?这显然可以随机化.计算前者的复杂度为$O ( nd )$,后者由于$C$很特殊,可以在$O ( n )$的时间内求出.这样我们就保证了算法复杂度上的合理性.

接下来,我们要证明其正确率上的合理性.这个算法显然是单侧错误的Monte Carlo算法.问题在于正确率:

令$D = B - C$,若返回相等但实际上不相等,则$D$中至少存在一个不为$0$的数字,假设$D_{ i , j } \ne 0$.我们令$E = X \times D$,那么只有当$E$是零向量时才会错误.而$E_j = \sum_{ k } X_k D_{ k , j }$,不难解得:$E_i = - \frac{ 1 }{ D_{ i , j } } \sum_{ k \ne i } X_k D_{ k , j }$,也就是说如果$X$的其它位置都确定了,那么$E$只有一种取值会返回错误.由于$k$一共就俩取值,所以正确率至少$\frac{ 1 }{ 2 }$.

至于找到答案:我们找到一个不为$0$的$E_i$,那么一定存在一组解包含了第$i$个向量,只需枚举另一个向量检验就行,复杂度$O ( nd )$.

$k = 3$的话,我们注意到$\mod 3$意义下,$1$和$2$的平方都是$1$.考虑$\sum_{ j } B_{ i , j }^2 X_j = \sum_{ j } B_{ i , j } X_j B_{ h , i }^T$,大概做做.

Las Vegas算法(Sherwood算法)

总是能返回正确的结果,但是其运行时间不确定.对于一些平均时间复杂度优秀,但是最坏情况下复杂度较高的确定性算法,通过引入随机函数,尝试减小最坏情况的可能性,以在期望意义下达到优秀的时间复杂度.

算法设计思路

设计一个能解决问题的确定性算法

这个算法需要枚举全排列.
通常,问题问的是要么只是可行解而不是最优解,要么最优方案特别多,总之要保证有用的排列个数不会太少

向算法引入随机化优化复杂度

随机化寻找排列来降低复杂度.
通常证明复杂度和正确率巨大麻烦,这里建议直接实践证明.

Example

快速排序算法

我们试图计算它的期望时间复杂度:

不妨设$T ( n )$表示对长度为$n$的序列运行快速排序算法所需的期望时间,我们有:

$\begin{aligned} T ( 0 ) & = 0 \\ T ( n ) & = n + \frac{ 1 }{ n } \sum_{ i = 0 }^{ n - 1 } ( T_i + T_{ n - i - 1 } ) \end{aligned}$

做放缩(可能有些地方需要$+ 1$或者$- 1$或者加取整,但是问题不大,反正是期望):

$\begin{aligned} T ( n ) & = n + \frac{ 1 }{ n } \sum_{ i = 0 }^{ n - 1 } ( T_i + T_{ n - i - 1 } ) \\ & = n + \frac{ 2 }{ n } \sum_{ i = \frac{ n }{ 2 } }^{ n - 1 } ( T_i + T_{ n - i - 1 } ) \\ & = n + \frac{ 2 }{ n } \sum_{ i = \frac{ n }{ 2 } }^{ \frac{ 3 n }{ 4 } } ( T ( i ) + T ( n - i - 1 ) ) + \frac{ 2 }{ n } \sum_{ i = \frac{ 3 n }{ 4 } }^{ n } ( T ( i ) + T ( n - i - 1 ) ) \end{aligned}$

由于$T ( n ) \geq n$,所以对于$\frac{ n }{ 2 } \leq i \leq j$,我们显然有:$T ( i ) + T ( n - i ) \leq T ( j ) + T ( n - j )$.

因此:

$\begin{aligned} T ( n ) & \leq n + \frac{ 2 }{ n } \sum_{ i = \frac{ n }{ 2 } }^{ \frac{ 3 n }{ 4 } } ( T ( \frac{ 3 n }{ 4 } ) + T ( \frac{ n }{ 4 } ) ) + \frac{ 2 }{ n } \sum_{ i = \frac{ 3 n }{ 4 } }^{ n } ( T ( n - 1 ) + T ( 0 ) ) \\ & \leq n + \frac{ 1 }{ 2 } ( T ( \frac{ 3 n }{ 4 } ) + T ( \frac{ n }{ 4 } ) + T ( n - 1 ) ) \end{aligned}$

我们要证明$\exists c$,$T ( n ) \leq cn \log n$,考虑使用数学归纳法,则:

$\begin{aligned} T ( n ) & \leq n + \frac{ 1 }{ 2 } ( \frac{ 3 cn }{ 4 } \log ( \frac{ 3 n }{ 4 } ) + \frac{ cn }{ 4 } \log ( \frac{ n }{ 4 } ) + c ( n - 1 ) \log ( n - 1 ) ) \\ & \leq n + c ( \frac{ 3 n }{ 8 } \log n - \frac{ 3 n }{ 8 } \log \frac{ 4 }{ 3 } + \frac{ n }{ 8 } \log n - \frac{ n }{ 4 } + \frac{ n }{ 2 } \log n ) \\ & = cn \log n + n ( 1 - \frac{ 3 c }{ 8 } \log ( \frac{ 4 }{ 3 } ) - \frac{ c }{ 4 } ) \end{aligned}$

于是显然存在,假设成立.

一类由Monte Carlo算法改造而成的算法

对于一类一定有解的构造性问题,假设我们有一个正确率为$p$,时间复杂度为$O ( f ( n ) )$的产生单侧错误的Monte Carlo算法,我们时图将其改造为Las Vegas算法,我们现在想知道它的期望复杂度.

设其期望运行$k$次,则:

$\begin{aligned} k & = \sum_{ i = 1 }^{ \infty } p ( 1 - p )^{ i - 1 } i \\ ( 1 - p ) k & = \sum_{ i = 1 }^{ \infty } p ( 1 - p )^i i \\ pk & = \sum_{ i = 2 }^{ \infty } p ( 1 - p )^{ i - 1 } = p \sum_{ i = 0 }^{ \infty } ( 1 - p )^i \\ k & = \frac{ 1 }{ p } \end{aligned}$

则期望复杂度为$O ( \frac{ f ( n ) }{ p } )$.

Example3(CF329C Graph Reconstruction)

Example4([Petrozavodsk Summer-2015. Moscow IPT Contest B]Game With A Fairy)

首先注意到一个问题:操作能得到的信息太少了,应该是没有什么确定性算法.因此考虑随机化,那就肯定要先将整个序列random_shuffle一下.

然后呢?我们考虑之后随机选取新序列的一个前缀询问,只要有大致的正确性/复杂性估计应该就是很正确的.

这里有一种方式:考虑这个前缀中第一个有宝藏的位置$x_1$和第二个位置$x_2$,显然只要问到$[ x_1 , x_2 )$是正确的.

考虑因为是随机,所以$x_1 \times 2 \leq x_2$的概率应当是不低的(事实上约为$\frac{ 1 }{ 2 }$),而此时的$[ x_1 , x_2 )$中必有一个位置是二的整数幂,因此我们查询一个等比数列:$1 , 2 , 4 , . . .$.每次random_shuffle后就查一次,就可以得到一个正确性较高的Las Vegas算法.

爬山与模拟退火

爬山

也就是随机一个起始的解,然后走向与其相邻的较大的解.

但是这样会卡在一个局部最优解上而得不到全局最优解.

于是我们就有了模拟退火算法.

模拟退火

简而言之,模拟退火就是以一定的概率跳到随机的不优秀的点,这样就避免卡在了局部最优解上.不妨设我们想找到最大解,如果要最小解那就稍微改改.

下面给出这个概率的公式:

$P = \begin{cases} 1 & E_{ t + 1 } > E_t \\ e^{ \frac{ E_{ t + 1 } - E_t }{ T } } & E_{ t + 1 } \leq E_t \end{cases}$

具体流程是,先设定一个初始温度$T_0$,降温速度$k \in ( 0 , 1 )$,以及终止温度$T_k$,每次操作后让$T = kT$,直到其小于终止温度.

数据随机下的性质

树

随机树树高为$\sqrt{ n }$.
点的度数期望为$\log n$.

数

数字的期望因数个数为$\log V$.

序列

随机序列的LIS长度期望为$O ( \sqrt{ n } )$.

概率与期望

发表于 2025-06-23 更新于 2025-12-27 分类于具体数学 Waline：

离散概率

基本定义

概率空间$\Omega$:在一个给定问题中可能发生的所有情况.

事件:$\Omega$的一个子集.

基本事件$\omega$:$\Omega$中的单个元素,也可以看作集合大小为$1$的事件.

概率:若$\omega \in \Omega$,我们称它发生的概率为$\Pr ( \omega )$,有$\Pr ( \omega ) \geq 0$且$\sum_{ \omega \in \Omega } \Pr ( \omega ) = 1$.

随机变量:在概率空间的基本事件上定义的函数.

联合分布:如果两个随机变量$X$和$Y$定义在同一个概率空间$\Omega$上,对于每一个在$X$取值范围内的$x$以及在$Y$取值范围内的$y$,我们称$\Pr ( X = x \land Y = y )$为它们的联合分布.

独立:如果对于每一个在$X$取值范围内的$x$以及在$Y$取值范围内的$y$,$\Pr ( X = x \land Y = y ) = \Pr ( X = x ) \times \Pr ( Y = y )$,我们称$X$和$Y$是独立的.

期望(均值)$E X$:我们设概率空间上的随机变量$X$的期望$EX = \sum_{ x \in X ( \Omega ) } x \times \Pr ( X = x ) = \sum_{ w \in \Omega } X ( \omega ) \Pr ( \omega )$.

中位数:我们设概率空间上的随机变量$X$的中位数为满足$\Pr ( X \leq x ) \geq 0 . 5 \land \Pr ( X \geq x ) \geq 0 . 5$的$x \in X ( \Omega )$所组成的集合.

众数:我们设概率空间上的随机变量$X$的众数为满足$\Pr ( X = x ) \geq \Pr ( X = x ‘ ) , \forall x ‘ \in X ( \Omega )$的$x \in X ( \Omega )$所组成的集合.

方差$VX$:我们设概率空间上的随机变量$X$的方差$VX = E ( ( X - EX )^2 )$.

标准差$\sigma$:我们设概率空间上的随机变量$X$的标准差$\sigma = \sqrt{ VX }$.

期望的简单运算

如果$X , Y$是定义在同一个概率空间上的两个随机变量,那么:

$E ( X + Y ) = EX + EY$.
$E ( \alpha X ) = \alpha EX$.
如果$X$和$Y$互相独立,那么$E ( XY ) = ( EX ) ( EY )$.

上述法则都可以通过期望的定义简单证明.

此外(3)的逆命题不成立.考虑取$X$分别以$\frac{1}{2}$的概率选取$-1$和$1$,取$Y=X^2$,则$E(X)=E(XY)=0$.

方差的简单运算

我们考虑方差的定义式:

$\begin{aligned} E ( ( X - EX )^2 ) & = E ( X^2 - 2 X ( EX ) + ( EX )^2 ) \\ & = E ( X^2 ) - 2 ( EX ) ( EX ) + ( EX )^2 \\ & = E ( X^2 ) - ( EX )^2 \end{aligned}$

也即:方差等于随机变量平方的均值减均值的平方.

当$X$和$Y$为独立的随机变量时,我们有:

$\begin{aligned} V ( X + Y ) & = E ( ( X + Y )^2 ) - ( EX + EY )^2 \\ & = E ( ( X + Y )^2 ) - ( EX )^2 - 2 ( EX ) ( EY ) - ( EY )^2 \end{aligned}$

而又有:

$\begin{aligned} E ( ( X + Y )^2 ) & = E ( X^2 + 2 XY + Y^2 ) \\ & = E ( X^2 ) + 2 ( EX ) ( EY ) + E ( Y^2 ) \end{aligned}$

则:

$\begin{aligned} V ( X + Y ) & = E ( X^2 ) + 2 ( EX ) ( EY ) + E ( Y^2 ) - ( EX )^2 - 2 ( EX ) ( EY ) - ( EY )^2 \\ & = VX + VY \end{aligned}$

即:独立随机变量之和的方差等于它们的方差之和.此外显然也有$\mathrm{Var}(X-Y)=\mathrm{Var}(X)+\mathrm{Var}(Y)$.

事实上,容易见到可以定义协方差$\mathrm{Cov}(X,Y)=E(XY)-E(X)E(Y)$.容易见到以下性质:

$\mathrm{Cov}(X,X)=\mathrm{Var}(X)$.
$\mathrm{Cov}(X,Y)=\mathrm{Cov}(Y,X)$.
$\mathrm{Cov}(aX,bY)=ab\mathrm{Cov}(X,Y)$.
$\mathrm{Cov}(X_1+X_2,Y)=\mathrm{Cov}(X_1,Y)+\mathrm{Cov}(X_2,Y)$.
若$X,Y$相互独立,则$\mathrm{Cov}(X,Y)=0$.然而逆命题不成立.
$\mathrm{Var}(\sum_{i}X_i)=\sum_{i}\sum_j\mathrm{Cov}(X_i,X_j)$.
$\mathrm{Var}(X+Y)=\mathrm{Var}(X)+\mathrm{Var}(Y)+2\mathrm{Cov}(X,Y)$.

随机抽样调查

如果我们随机取得了$n$个值$X_1 , X_2 , . . . , X_n$,那么我们可以通过这些值来估计概率空间的期望和方差.

$\hat EX = \cfrac{ \sum_{ i = 1 }^n X_i }{ n }$.

$\hat VX = \cfrac{ \sum_{ i = 1 }^n X_i^2 }{ n - 1 } - \cfrac{ ( \sum_{ i = 1 }^n X_i )^2 }{ n ( n - 1 ) }$.

这里的$\hat VX$似乎与定义不是那么相符.但是它拥有更好的性质:$E ( \hat VX ) = VX$.

证明如下:

$\begin{aligned} E ( \hat VX ) & = \cfrac{ 1 }{ n - 1 } E ( \sum_{ i = 1 }^n X_i^2 - \cfrac{ 1 }{ n } \sum_{ j = 1 }^n \sum_{ k = 1 }^n X_j X_k ) \\ & = \cfrac{ 1 }{ n - 1 } ( \sum_{ i = 1 }^n E ( X_i^2 ) - \cfrac{ 1 }{ n } \sum_{ i = 1 }^n \sum_{ j = 1 }^n E ( X_i X_j ) ) \\ & = \cfrac{ 1 }{ n - 1 } ( \sum_{ i = 1 }^n E ( X^2 ) - \cfrac{ 1 }{ n } \sum_{ i = 1 }^n \sum_{ j = 1 }^n ( ( EX )^2 [ j \ne k ] + E ( X^2 ) [ j = k ] ) ) \\ & = \cfrac{ 1 }{ n - 1 } ( nE ( X^2 ) - \cfrac{ 1 }{ n } ( nE ( X^2 ) + n ( n - 1 ) ( EX )^2 ) ) \\ & = E ( X^2 ) - ( EX )^2 \\ & = VX \end{aligned}$

条件概率

已知事件B发生时事件A发生的概率为$P ( A | B ) = \frac{ P ( AB ) }{ P ( B ) } \\$.

贝叶斯公式

贝叶斯公式:如果有$\{ B_i \}$是样本空间的一个划分,即$\forall i , j$,有$B_i \cap B_j = \emptyset$,并且有$\bigcup_{ i = 1 }^n B_i = \Omega$.则有$P ( B_i | A ) = \frac{ P ( AB_i ) }{ P ( A ) } = \frac{ P ( AB_i ) }{ P ( A ) \sum P ( B_j ) } = \frac{ P ( A B_i ) }{ \sum_{ j = 1 }^n P ( A B_j ) } = \frac{ P ( A | B_i ) P ( B_i ) }{ \sum_{ j = 1 }^n P ( A | B_j ) P ( B_j ) } \\$.

简化形式:$P ( B | A ) = \frac{ P ( A | B ) P ( B ) }{ P ( A ) } \\$.

另外,我们考虑设$O ( B ) = \cfrac{ P ( B ) }{ P ( \lnot B ) }$,称$\cfrac{ P ( B | E ) }{ P ( \lnot B | E ) }$为贝叶斯算子,则同理可得:

$O ( B | E ) = O ( B ) \cfrac{ P ( B | E ) }{ P ( \lnot B | E ) }$

这个公式更加精准地分开了先验概率和后验概率,也表现了贝叶斯算子对先验概率的改变.

概率生成函数

如果$X$是定义在概率空间$\Omega$上的随机变量,那么它的概率生成函数为$G_X ( z ) = \sum_{ k \geq 0 } \Pr ( X = k ) z^k = E ( z^X )$.

不难发现$G_X ( z )$需要满足的条件:所有系数都非负并且$G_X ( 1 ) = 1$.

我们发现,当我们定义了概率生成函数后,期望和方差都可以使用它来表示:

$\begin{aligned} EX & = G_X ' ( 1 ) \\ E ( X^2 ) & = G ' '_X ( 1 ) + G_X ' ( 1 ) \\ VX & = G_X ' ' ( 1 ) + G_X ' ( 1 ) - ( G_X ' ( 1 ) )^2 \end{aligned}$

通常,我们也可以将方差和均值的定义扩展到任意函数上,于是我们定义:

$\begin{aligned} Mean ( G ) & = G ' ( 1 ) \\ Var ( G ) & = G ' ' ( 1 ) + G ' ( 1 ) - ( G ' ( 1 ) )^2 \end{aligned}$

不过,求导的过程可能会有些麻烦,但我们可以直接使用泰勒定理:

$G ( 1 + t ) = \sum_{ i \geq 0 } \cfrac{ G^{ ( i ) } ( 1 ) }{ i ! } t^i$

另外,我们不难发现:$G_{ X + Y } ( z ) = G_X ( z ) G_Y ( z )$.

根据前面的推导,我们有:

$\begin{aligned} Mean ( G_{ X + Y } ) & = Mean ( G_X ) + Mean ( G_Y ) \\ Var ( G_{ X + Y } ) & = Var ( G_X ) + Var ( G_Y ) \end{aligned}$

换句话说,若$G_X ( 1 ) = 1 , G_Y ( 1 ) = 1$,那么这个式子与直接对$G_{ X + Y }$使用求导的那个公式是等价的.注意,这里并没有要求这些生成函数的系数是非负的.

于是我们有了另一个法则:

$\begin{aligned} Mean ( G_X ) & = Mean ( G_{ X + Y } ) - Mean ( G_Y ) \\ Var ( G_X ) & = Var ( G_{ X + Y } ) - Var ( G_Y ) \end{aligned}$

Example1

一枚硬币正面向上的概率为$p$,反面向上的概率为$q$,设硬币正面向上为H,反面向上为T,不断抛掷硬币直到抛掷出连续的THTTH为止,求期望次数.

考虑设$N$为所有不包含THTTH的硬币序列的生成函数,$S$为所有只有结尾为THTTH的硬币序列的生成函数,令$H = pz , T = qz$,$1$为空集,我们显然有:

$\begin{aligned} 1 + N \times ( H + T ) & = N + S \\ N \times THTTH & = S + S \times TTH \end{aligned}$

解方程即可.

另外不难发现,这种方法取决于字符串的所有border,显然是通用方法.

我们考虑扩展这个方法,设$A$是我们要找到的字符串,$m$是它的长度,令$A^{ ( k ) }$表示$A$字符串的前$k$个字符所组成的字符串,$A_{ ( k ) }$表示$A$字符串的后$k$个字符所组成的字符串.这样的形式与$k$阶导的形式可能会起冲突,但至少在接下来我们的式子中不会出现导数~~(好吧其实是因为《具体数学》上就这么写的我也懒得改了)~~.

我们的方程将会变为:

$\begin{aligned} 1 + N ( H + T ) & = N + S \\ N \times A & = S ( \sum_{ k = 0 }^{ m - 1 } A^{ ( k ) } [ A^{ ( m - k ) } = A_{ ( m - k ) } ] ) \end{aligned}$

如果我们设$\tilde{ A }$为将字符串$A$中的H替换成$\cfrac{ 1 }{ p } z$,T替换成$\cfrac{ 1 }{ q } z$之后的值,那么显然有:

$\begin{aligned} N \times A & = A \times S \times ( \sum_{ k = 1 }^{ m } \tilde{ A }_{ ( k ) } [ A^{ ( k ) } = A_{ ( k ) } ] ) \\ N & = S \times ( \sum_{ k = 1 }^{ m } \tilde{ A }_{ ( k ) } [ A^{ ( k ) } = A_{ ( k ) } ] ) \\ \cfrac{ S - 1 }{ H + T - 1 } & = S \times ( \sum_{ k = 1 }^{ m } \tilde{ A }_{ ( k ) } [ A^{ ( k ) } = A_{ ( k ) } ] ) \\ S \times ( 1 + ( 1 - H - T ) \times ( \sum_{ k = 1 }^{ m } \tilde{ A }_{ ( k ) } [ A^{ ( k ) } & = A_{ ( k ) } ] ) ) = 1 \end{aligned}$

这显然是一个卷积的形式.

令$w = \sum_{ k = 1 }^{ m } \tilde{ A }_{ ( k ) } [ A^{ ( k ) } = A_{ ( k ) } ]$.

令$H ( z ) = 1$,$F ( z ) = ( 1 + ( 1 - z ) \times w )$,$G ( z ) = S$.

那么我们显然可以直接求$G ( z )$的期望和方差,事实上:

$\begin{aligned} EX & = \sum_{ k = 1 }^{ m } \tilde{ A }_{ ( k ) } [ A^{ ( k ) } = A_{ ( k ) } ] \\ VX & = ( EX )^2 - \sum_{ k = 1 }^m ( 2 k - 1 ) \tilde{ A }_{ ( k ) } [ A^{ ( k ) } = A_{ ( k ) } ] \end{aligned}$

如果硬币是均匀的($p = q = \cfrac{ 1 }{ 2 }$)我们引入另一个符号:我们设$A : A = \sum_{ k = 1 }^m 2^{ k } [ A^{ ( k ) } = A_{ ( k ) } ]$.那么显然期望需要的抛硬币次数就是$( A : A )$.

Example2(Penney游戏)

一枚均匀硬币,设硬币正面向上为H,反面向上为T.不断扔硬币直到扔出连续的HHT或HTT为止,求最后以HHT结尾的概率.

我们设$S_A$为所有以HHT结尾的硬币序列的生成函数,设$S_B$为所有以HTT结尾的硬币序列的生成函数.$N$为其它的硬币序列的生成函数,令$H = T = 0 . 5 z$.

我们显然有:

$\begin{aligned} 1 + N ( H + T ) & = N + S_A + S_B \\ N \times HHT & = S_A \\ N \times HTT & = S_A \times T + S_B \end{aligned}$

解方程并带入$z = 1$,可以有得知以HHT结尾的概率为$\cfrac{ 2 }{ 3 }$.

事实上,我们使用类似Example1的方法,设这两个硬币序列分别为$A$和$B$,那么可以求出:

$\cfrac{ S_A }{ S_B } = \cfrac{ B : B - B : A }{ A : A - A : B }$

Example3([SDOI2017] 硬币游戏)

是Example2的超级加强版.

把上面的东西给形式化一下,不妨设$g_i$表示进行了$i$步还未结束的概率,$f_{ k , i }$为进行了$i$步恰好第$k$个人胜利的概率,$F , G$是它们的生成函数,我们自然有:

$1 + xG ( x ) = \sum_k F_k ( x ) + G ( x )$.
$( \frac{ 1 }{ 2 } x )^L G ( x ) = \sum_{ j = 1 }^n F_j ( x ) \sum_{ i = 0 }^{ L - 1 } ( \frac{ 1 }{ 2 } x )^i [ A_k^{ ( L - i ) } ={ A_j }_{ ( L - i ) } ]$.

第一个式子的用处在于带入$x = 1$,发现$\sum_{ k } F_k ( 1 ) = 1$.

把(2)化简一下,有:

$\begin{aligned} x^L G ( x ) & = \sum_{ j = 1 }^n F_j ( x ) \sum_{ i = 0 }^{ L - 1 } ( \frac{ 1 }{ 2 } x )^{ i - L } [ A_k^{ ( L - i ) } ={ A_j }_{ ( L - i ) } ] \\ x^L G ( x ) & = \sum_{ j = 1 }^n F_j ( x ) \sum_{ i = 1 }^{ L } ( \frac{ 1 }{ 2 } x )^{ - i } [ A_k^{ ( i ) } ={ A_j }_{ ( i ) } ] \end{aligned}$

带入$x = 1$,有:

$G ( 1 ) = \sum_{ j = 1 }^n F_j ( 1 ) \sum_{ i = 1 }^{ L } 2^i [ A_k^{ ( i ) } ={ A_j }_{ ( i ) } ]$

不难发现对于不同的$k$,(2)的右边不同,而左边一定相同,这样就给出了$n$个等式,算上(1)一共有$n + 1$个等式,可以算出$G ( 1 ) , F_{ 1 \cdots n } ( 1 )$这$n + 1$个未知数.

二项式分布

现在有一个大小为$n + 1$的概率空间,其中$\Pr ( \omega_k ) = \binom{ n }{ k } p^k q^{ n - k } \\$,我们把这样的概率序列称为二项式分布.

如果我们令$H ( z ) = q + pz$,不难发现二项式分布的生成函数为$H ( z )^n$.

不难发现,满足二项式分布的随机变量的均值是$np$,方差是$npq$.

与二项式分布相对应的还有负二项式分布,它的生成函数形如:$G ( z )^n = ( \cfrac{ p }{ 1 - qz } )^n = \sum_{ k } \binom{ n + k - 1 }{ k } p^n q^k z^k$.

我们考虑如何求$G ( z )$的方差和均值,不妨设$F ( z ) = \cfrac{ 1 - qz }{ p } = \cfrac{ 1 }{ p } - \cfrac{ q }{ p } z$,则$G ( z )^n = F ( z )^{ - n }$.

不难发现$F ( z )$满足二项式分布.也就是说,以$( n , p , q )$为参数的负二项式分布也就是以$( - n , - \cfrac{ q }{ p } , \cfrac{ 1 }{ p } )$为参数的二项式分布.

模型

树上随机游走

随机游走指每次从相邻的点中随机选一个走过去，重复这样的过程若干次.

Example1

给一棵所有边长都为$1$的$n$个点的树,问所有点对$( i , j ) ( 1 \leq i , j \leq n )$中,从$i$走到$j$的期望距离的最大值是多少.

由于树上简单路径唯一,我们考虑设$f_u$表示$u$随机走到它父亲的期望,$g_v$表示$v$的父亲(假设是$u$)走到$v$的期望.

对于$f_u$,我们有:

$\begin{aligned} f_u & = \cfrac{ \sum_{ u \rightarrow v } ( f_v + f_u ) }{ \deg_u } + 1 \\ f_u & = \deg_u + \sum_{ u \rightarrow v } f_v \end{aligned}$

对于$g_v$,我们有:

$\begin{aligned} g_v & = \cfrac{ g_u + g_v + \sum_{ u \rightarrow w , w \ne v } ( g_v + f_w ) }{ \deg_u } + 1 \\ g_v & = g_u + \sum_{ u \rightarrow w , w \ne v } f_w + \deg_u \end{aligned}$

Example2

给出一棵$n$个节点的树,每个点有可能是黑白两种颜色的一种.

现在从$1$号点开始随机游走(即走这个点的每条出边的概率是相同的),每到一个点,如果这个点是黑点,或者这是白点并且这个点第一次经过,那么答案$+ 1$.当走到度数为$1$的节点时游走停止.

注意到黑白点对答案的贡献是互相独立的,所以分开讨论:

如果只有黑点,那么显然答案就是路径的期望长度,我们设$f_u$表示以$u$为起点的路径的期望长度,不难注意到$f_{ leaf } = 1$且$f_u = 1 + \cfrac{ 1 }{ \deg_u } \sum_{ u \rightarrow v \lor v \rightarrow u } f_v$.这个dp转移显然是有后效性的,可以使用高斯消元做,但有一个经典做法:我们求得$f_u = k_u f_{ fa } + b_u$,然后就可以采取带入化简的方法做了.

如果只有白点,考虑每个点只会贡献一次,所以我们要求出的就是每个点被走到的概率.注意到一个点被走到一定是从它父亲走来的,于是我们需要求出$g_v$表示从$v$的父亲(假设是$u$)走到$v$的概率,再令$f_u$表示从$u$走到父亲的概率,类似Example1,我们有:

$\begin{aligned} f_u & = \cfrac{ 1 }{ \deg_u } ( 1 + \sum_{ u \rightarrow v } f_v f_u ) \\ g_v & = \cfrac{ 1 }{ \deg_u } ( 1 + g_v g_u + \sum_{ u \rightarrow w , w \ne v } f_w g_v ) \end{aligned}$

最后把两部分答案合起来就好.

计数与期望的转换

Example(CodeChef Secplayer)

冷静一下,如果我们直接计数的话会发现巨大难做,因为项太多了,直接乘起来也太麻烦了.

这启发我们:当我们注意到一个计数题的各种情况相乘很麻烦的时候,我们不妨只考虑一种情况并计算期望,然后拿期望和总数反推计数.注意到权值最小的人最危险,他不能和其他任何一个人匹配到,不然就死了.那不难求得此时他作为次大值存活的概率为$\frac{ 1 }{ \binom{ n }{ 2 } }$.

把所有人权值从大到小排序,设$f_i$表示只考虑前$i$个人的时候的期望,不难发现:$f_{ i } = \frac{ 1 }{ \binom{ i }{ 2 } } v_i + ( 1 - \frac{ 1 }{ \binom{ i }{ 2 } } ) f_{ i - 1 }$.

一些小技巧

Example1(CF865C)

首先写出转移式子,但是存在后效性.如果我们设$f_{ i , j }$表示过了$i$关,花费为$j$的期望,不难发现所有的$f$都需要与$f_{ 0 , 0 }$取$\min$,这咋办?

我们考虑二分这个$f_{ 0 , 0 }$,做的时候直接取$\min$,这样最后还会求出一个$f_{ 0 , 0 }$,比较一下大小然后继续做二分.

等一下,为撒子这样是收敛的呢?

首先,根据这个题,期望肯定是存在的.

我们注意到我们一开始二分的$f_{ 0 , 0 }$越大,最后的答案就越大,但是增长的一定会变慢.换句话说,最后的答案关于我们二分的值的关系应该是一个上凸的函数(增长的时候会被取$\min$的另一项限制住,但原本应该是没被限制的),于是这个时候得到的答案如果比二分的答案更小,那我们就应该调小一点.

换句话说,当我们二分答案的时候,应该判断函数凸性.wqs二分也是这个道理:二分答案并判断答案是否满足条件.

Example2(猎人杀)

先做一步转化:如果做期望的时候,会有一些操作变得不能做,那我们改为:先随便选,如果选到不合法的操作就跳过,概率和期望都不会变.

offline

Example3(AGC019F)

人类智慧题…

首先注意到策略显然是每次选剩下最多的答案.

我们画一张$n \times m$的图(假设$n \geq m$),其中格点$( a , b )$表示现在还剩$a$个Yes,$b$个No.我们再把我们的策略用图上的有向边表示.我们先考虑转化为计数问题,那答案显然就是所有从$( n , m )$走到$( 0 , 0 )$的路径与我们图上有向边的交的大小总和.

然后咧?

我们注意到这张图长得太规律了,换句话说,如果我们把图的左半部分沿着直线$y = x$翻折(路径也跟着翻折),注意到对着这张图做仍然是一样的!

所以呢?由于从$( n , m )$走到$( 0 , 0 )$一定会经过$n$条有向边,所以期望贡献一定要加上一个$n$.而如果我走到了直线$y = x$上,那接下来的贡献是$\frac{ 1 }{ 2 }$.我们只需要枚举一下走到了多少次即可.

一些不等式

Union Bound

即:$\mathbb{P} [ \bigcup_i X_i ] \leq \sum \mathbb P [ X_i ]$,取等当且仅当所有$X_i$互斥.

Markov 不等式

若$X \geq 0$,则$\mathbb{P} [ X \geq t \mathbb{ E } [ X ] ] \leq \frac{ 1 }{ t }$.

显然,多的太多的话就会超过$E$.

Chebyshev 不等式

当$\sigma(X)>0$时,有

$\mathbb{P}(|X-\mathbb{E}(X)|\geq c\sdot \sigma(X))\leq \frac{1}{c^2}$

证明的话直接考虑设$Y=(X-\mathbb E(X))^2$,用Markov不等式得到:

$\begin{aligned} \mathbb{P}(Y\geq c^2\mathbb E(Y))&\leq \frac{1}{c^2}\\ \mathbb{P}((X-\mathbb E(X))^2\geq c^2\sigma^2(X))&\leq \frac{1}{c^2}\\ \mathbb{P}|(X-\mathbb E(X)|\geq c\sigma(X))&\leq \frac{1}{c^2}\\ \end{aligned}$

一些离散分布

泊松分布

取二项分布的极限情况.设此时$n=\lambda m$,每个东西有$\frac{1}{m}$的概率选入,则对于一个固定的常数$k$,当$m\to \infty$的时候,$P(X=k)=\frac{1}{k!}\lambda^k e^{-\lambda}$,记作$X\sim \pi(\lambda)$.

欸,虽然我们这里只考虑了$k$某种程度上远小于$m$的存在,但好在大的部分也不会有什么太大影响,因此:

$\sum_k P(X=k)=1$

原因是$e^{\lambda}=\sum_k \frac{\lambda^k}{k!}$.

此时来看$\mathbb E(X)$,留神到无非是上面那个东西转移了一下子,因此$\mathbb{E}(X)=\lambda$.

来看$\mathbb{E}(X^2)$,自然有:

$\begin{aligned} &\sum_k \frac{1}{k!}\lambda^k e^{-\lambda}k^2\\ =&\sum_k \frac{1}{k!}\lambda^k e^{-\lambda}k(k-1)+\sum_k \frac{1}{k!}\lambda^k e^{-\lambda}k\\ =&\lambda^2+\lambda \end{aligned}$

所以$\sigma^2(X)=\mathbb{E}(X^2)-(\mathbb E(X))^2=\lambda$.

几何分布

伯努利试验中首次发生结果$A$的次数,记作$X\sim \text{G}(p)$.

显然$P(X=k)=p(1-p)^{k-1}$,此外$P(X>n)=(1-p)^n$.

设$f(p)=\sum_{k\geq 1}(1-p)^{k-1}$,则$f(p)=\frac{1}{p}$,$E(X)=-pf’(p)=\frac{1}{p}$,$\sigma^2(X)=\frac{1-p}{p^2}$.

很重要的一个性质是无记忆性.即$P(X>m+n|X>m)=P(X>n)$.

负二项分布

伯努利实验中结果$A$发生$r$次的重复次数.则$P(X=k)=\binom{k-1}{r-1}p^r(1-p)^{k-r}$,记作$X\sim \text{NB}(r,p)$.显然$\text{NB}(1,p)\sim \text{G}(p)$.必然有$E(X)=\frac{r}{p}$.

首先要验证:

$\begin{aligned} \sum_{k\geq r}P(X=k)&=\sum_{k\geq r}\binom{k-1}{r-1}p^r(1-p)^{k-r}\\ &=\sum_{l\geq 0}\binom{l+r-1}{r-1}p^r(1-p)^l\\ &=\sum_{l\geq 0}\binom{l+r-1}{l}p^r(1-p)^l \end{aligned}$

而:

$\begin{aligned} p^{-r}&=(1-(1-p))^{-r}\\ &=\sum_{l\geq 0}\binom{-r}{l}(-1)^l(1-p)^{l}\\ &=\sum_{l\geq 0}\binom{l+r-1}{l}(1-p)^l \end{aligned}$

连续随机变量

给定随机变量$X$和实数$x$,定义$F(x)=P(X\leq x)$为随机变量$X$的分布函数.

分布函数有如下性质:

有界性:$0\leq F(x)\leq 1$,而且$\lim_{x\to -\infty}F(x)=0,\lim_{x\to +\infty}F(x)=1$.
单调性:$F(x)$单调不减.
右连续:$F(x_0+0)=F(x_0)$.

如果存在一个$f(x)$,使得$F(x)=\int_{-\infty}^x f(x)\mathrm{d}x$,则称$X$是连续随机变量,而$f(x)$是其概率密度函数.它还应当满足以下性质:

非负性:$f(x)\geq 0$.
正则性:$\int_{-\infty}^{+\infty}f(t)\mathrm{d}t=1$.

对于连续随机变量.此时$F$还满足左连续$F(x_0-0)=F(x_0)$.

由此还可以得出连续随机变量在任何一点处取值必然为零,因为$P(a\leq X\leq a)=P(a<X<a)=0$.

由此可以定义期望:当$\int_{-\infty}^{+\infty}f(x)|x|\mathrm{d}x<\infty$,则定义$E(X)=\int_{-\infty}^{+\infty}xf(x)\mathrm{d}x$.注意这里要求的是绝对可积而不是可积.

现在我们来搞定:$P(X\leq E(X))>0$.

策略是反证:如果$P(X\leq E(X))=0$.此时任取一个$\epsilon>0$使得$P(X\leq E(X)+\epsilon)\leq \frac{1}{2}$.

此时$E(X)\geq P(X\geq E(X)+\epsilon)(E(X)+\epsilon)+P(X< E(X)+\epsilon)E(X)>E(X)$,这就矛盾了.

接下来来做Markov不等式,对于非负随机变量$X$,若$E(X)> 0,a>0$,则$P(X\geq aE(X))\leq \frac{1}{a}$.原因是:

$\begin{aligned} E(X)&=\int_{-\infty}^{+\infty}f(x)x\mathrm{d}x\\ &\geq \int_{aE(X)}^{+\infty}f(x)x\mathrm{d}x\\ &\geq \int_{aE(X)}^{+\infty}f(x)aE(X)\mathrm{d}x\\ &=aE(X)\int_{aE(X)}^{+\infty}f(x)\mathrm{d}x\\ &=aE(X)P(X\geq aE(X)) \end{aligned}$

此时还可以定义$\mathrm{Var}(X)=E((X-E(X))^2)=E(X^2)-E^2(X)$.

Chebyshev不等式的证明只依赖于Markov不等式,因此在这里也能用.

高斯分布

概率密度函数$f(x)=\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}$.

除了上述已经提到的性质,它还满足:

对称性:$f(x)=f(-x)$.
$f(x)_{\max}=f(0)$.
$\lim_{x\to -\infty}f(x)=\lim_{x\to +\infty}f(x)=0$.
$E(X)=\int_{-\infty}^{+\infty}f(x)x\mathrm{d}x=0$.
$E(X^2)=\int_{-\infty}^{+\infty}f(x)x^2\mathrm{d}x=1$.
$\mathrm{Var}(X)=1$.

其中(5)的证明见:

$\begin{aligned} \int_{-\infty}^{+\infty}f(x)x^2\mathrm{d}x&=\int_{-\infty}^{+\infty}\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}x^2\mathrm{d}x\\ &=\int_{-\infty}^{+\infty}\frac{1}{\sqrt{2\pi}}(-x)\mathrm{d}e^{-\frac{x^2}{2}}\\ &=\frac{1}{\sqrt{2\pi}}(-x)e^{-\frac{x^2}{2}}|_{-\infty}^{+\infty}+\int_{-\infty}^{+\infty}\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}\mathrm{d}x\\ &=1 \end{aligned}$

还可以对此进行推广,考虑$f(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}}$,记$X\sim N(\mu,\sigma^2)$.只需取$y=\frac{x-\mu}{\sigma}$,就可以转换回标准正态分布,并且此时$F_Y(y)=F_X(\sigma y+\mu)$.

指数分布

对于$\lambda>0$,定义概率密度函数$f(x)=\begin{cases}\lambda e^{-\lambda x}&x\geq 0\\0&x<0\end{cases}$,记作$x\sim \mathrm{exp}(\lambda)$.其分布函数$f(x)="\begin{cases}1-e^{-\lambda" x}&x>0\\0&X\leq 0\end{cases}$.

它同样也有无记忆性.考虑$P(X>t)=e^{-\lambda t}$,从而$P(X>s+t|X>s)=P(X>t)$.

伽马分布

对于$\alpha>0$,定义伽马函数$\Gamma(\alpha)=\int_0^{+\infty}x^{\alpha-1}e^{-x}\mathrm{d}x$.我们见过很多次这个东西了,请看:

$\Gamma(1)=1$.
$\Gamma(\frac{1}{2})=\sqrt{\pi}$.
$\Gamma(\alpha+1)=\alpha\Gamma(\alpha)$.
$\Gamma(n+1)=n!$.
$\Gamma(n+\frac{1}{2})=\frac{(2n)!}{4^nn!}\sqrt \pi$.

对于$\lambda,\alpha>0$,定义概率密度函数$f(x)=\begin{cases}\frac{\lambda^\alpha}{\Gamma(\alpha)}x^{\alpha-1}e^{-\lambda x}&x\geq 0\\0&x<0\end{cases}$,称此时$x$符合伽马分布,记作$X\sim \Gamma(\alpha,\lambda)$.

先把正则性验证了吧,令$y=\lambda x$,则$f(x)=\frac{\lambda}{\Gamma(\alpha)}y^{\alpha-1}e^{-y}$,则$f(x)\mathrm{d}x=\frac{1}{\Gamma(\alpha)}y^{\alpha-1}e^{-y}\mathrm{d}y$,于是搞定了.

然后是其期望:

$\begin{aligned} E(X)&=\int_{0}^{+\infty}xf(x)\mathrm{d}x\\&=\int_0^{+\infty}\frac{1}{\Gamma(\alpha)}y^{\alpha}e^{-y}\frac{\mathrm{d}y}{\lambda}\\ &=\frac{\Gamma(\alpha+1)}{\Gamma(\alpha)\lambda}\\ &=\frac{\alpha}{\lambda} \end{aligned}$

类似地,$\int_0^{+\infty}x^2f(x)\mathrm{d}x=\frac{\Gamma(\alpha+2)}{\Gamma(\alpha)\lambda^2}$,从而算出$\mathrm{Var}(X)=\frac{\alpha}{\lambda^2}$.显然当$X\sim \Gamma(\alpha,\lambda)$时，$Y=kX\sim \Gamma(\alpha,\frac{\lambda}{k})$.

当$\alpha=1$的时候,我们得到了指数分布$\Gamma(1,\lambda)\sim \mathrm{Exp}(\lambda)$.

另一个特例是,$\alpha=\frac{n}{2},\lambda=\frac{1}{2}$.此时我们称其为自由度为$n$的卡方$\chi^2$分布.记作$\chi^2(n)$,其数学期望为$n$,方差为$2n$.当$n=1$的时候,$f(x)=\sqrt \frac{1}{2\pi x}e^{-\frac{x}{2}}$.

多维离散随机变量

重期望公式

考虑把$E(X|Y)$视作一个$g(Y)$,则$E(E(X|Y))=E(X)$.原因是$E(E(X|Y))=\sum_j P(Y=y_j)E(X|Y=y_j)$.

多维连续随机变量

设$F(x,y)=P(X\leq x\land Y\leq y)$.应该有:

联合分布函数有如下性质:

有界性:$0\leq F(x,y)\leq 1$,而且$\lim_{x\to -\infty}F(x,y)=\lim_{y\to -\infty}F(x,y)=0,\lim_{x,y\to +\infty}F(x,y)=1$.
单调性:当$x_1\leq x_2$时,$F(x_1,y)\leq F(x_2,y)$;当$y_1\leq y_2$时,$F(x,y_1)\leq F(x,y_2)$.
右连续:$F(x_0+0,y)=F(x_0,y)$,$F(x,y_0+0)=F(x,y_0)$.
非负性:$P(a<X\leq b,c<Y\leq d)=F(b,d)-F(a,d)-F(b,c)+F(a,c)\geq 0$.

当$F$连续时,如果能找到函数$f\geq 0$满足$F(x,y)=\int_{-\infty}^x\int_{-\infty}^y f(u,v)\mathrm{d}v\mathrm{d}u$,称$f$为联合密度函数.

接下来来看条件分布函数和条件密度函数,当概率密度函数的确连续时,定义:

$\begin{aligned} P(X\leq x|Y=y)&=\lim_{\Delta\to +0}P(X\leq x|y\leq Y\leq y+\Delta)\\ &=\lim_{\Delta\to +0}\cfrac{\int_{-\infty}^x\int_{y}^{y+\Delta}f(u,v)\mathrm{d}v\mathrm{d}u}{\int_{y}^{y+\Delta}f_Y(v)\mathrm{d}v}\\ &=\lim_{\Delta\to +0}\cfrac{\int_{-\infty}^x(\frac{1}{\Delta}\int_{y}^{y+\Delta}f(u,v)\mathrm{d}v)\mathrm{d}u}{\frac{1}{\Delta}\int_{y}^{y+\Delta}f_Y(v)\mathrm{d}v}\\ &=\cfrac{\int_{-\infty}^xf(u,y)\mathrm{d}u}{f_Y(y)}\\ &=\int_{-\infty}^x\cfrac{f(u,y)}{f_Y(y)}\mathrm{d}u\\ \end{aligned}$

其中$f_Y(y)=\int_{-\infty}^{+\infty}f(u,y)\mathrm{d}u$.

当$\forall x,y$都有$f(x,y)=f_X(x)f_Y(y)$,则称$X,Y$相互独立.

容易检验$E(X+Y)=E(X)+E(Y)$,而且当$X,Y$相互独立的时候,$E(XY)=E(X)E(Y)$,于是自然也有$\mathrm{Var}(X\pm Y)=\mathrm{Var}(X)+\mathrm{Var}(Y)$.

二维正态分布

即:

$f(x,y)=\frac{\exp(-\frac{1}{2(1-\rho^2)}\left(\frac{(x-\mu_1)^2}{\sigma_1^2}+\frac{(y-\mu_2)^2}{\sigma_2^2}-\frac{2\rho(x-\mu_1)(y-\mu_2)}{\sigma_1\sigma_2}\right))}{2\pi \sigma_1\sigma_2\sqrt{1-\rho^2}}$

现在来验证正则性,取$u=\frac{\frac{x-\mu_1}{\sigma_1}-\rho \frac{y-\mu_2}{\sigma_2}}{\sqrt{1-\rho^2}},v=\frac{y-\mu_2}{\sigma_2}$.而$\left|\frac{\partial(u,v)}{\partial(x,y)}\right|=\sigma_1\sigma_2\sqrt{1-\rho^2}$.于是:

$\begin{aligned} &\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}f(x,y)\mathrm{d}x\mathrm{d}y\\ =&\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}\frac{1}{2\pi}\exp\left(-\frac{1}{2}(u^2+v^2)\right)\mathrm{d}u\mathrm{d}v\\ =&1 \end{aligned}$

此外请看:

$\begin{aligned} f_X(x)&=\int_{-\infty}^{+\infty}f(x,y)\mathrm{d}y\\ &=\sigma_2\sqrt{1-\rho^2}\int_{-\infty}^{+\infty}f(x,y)\mathrm{d}u\\ &=\frac{1}{\sigma_1\sqrt{2\pi}}\exp\left(-\frac{(x-\mu_1)^2}{2\sigma_1^2}\right) \end{aligned}$

于是当$X,Y\sim N(\mu_1,\mu_2,\sigma_1^2,\sigma_2^2,\rho)$,则$X\sim N(\mu_1,\sigma_1^2),Y\sim N(\mu_2,\sigma_2^2)$.

此外:

$\begin{aligned} f(x|y)&=\frac{f(x,y)}{f_Y(y)}\\ &=\frac{1}{\sigma_1\sqrt{2\pi}\sqrt{1-\rho^2}}\exp\left(-\frac{1}{2(1-\rho^2)}\left(\frac{x-\mu_1}{\sigma_1}-\rho\frac{y-\mu_2}{\sigma_2}\right)^2\right) \end{aligned}$

也就是说,当$Y=y$时,$X\sim N(\mu_1+\rho\frac{\sigma_1}{\sigma_2}(y-\mu_2),\sigma_1^2(1-\rho^2))$,容易见到相互独立当且仅当$\rho=0$.

Example1

设$n\times n$的矩阵$A$中每个元素独立服从$N(0,1)$.求$E(\det A),E(\mathrm{trace}(A)),E(\mathrm{trace}(A^2))$.

考虑$\det A=\sum_{\sigma}\mathrm{sgn}(\sigma)\prod A_{i,\sigma(i)}$.直接套期望就知道$E(\det A)=0$.

显然$E(\mathrm{trace}(A))=0$.

而$E(\mathrm{trace}(A^2))$中,每一个$(A^2)_{i,i}=\sum_{j}E(a_{i,j}a_{j,i})=1$,于是$E(\mathrm{trace}(A^2))=n$.

重期望公式

定义$E(X|Y=y)=\int_{-\infty}^{+\infty}f(x|y)x\mathrm{d}x$.则$E(E(X|Y))=E(X)$.

协方差

和离散时的基本全部一样.其实早该看出来协方差就是一种双线性形式.

Example1

证明二维正态分布的$\mathrm{Cov}(X,Y)=\sigma_1\sigma_2\rho$.

容易见到:

$\begin{aligned} \mathrm{Cov}(X,Y)&=\int\int f(x,y)(x-\mu_1)(y-\mu_2)\mathrm{d}x\mathrm{d}y\\ &=\int\int\frac{1}{2\pi}\exp\left(-\frac{1}{2}(u^2+v^2)\right)\sigma_1\sigma_2v(u\sqrt{1-\rho^2}+\rho v)\mathrm{d}u\mathrm{d}v \end{aligned}$

然而:

$\begin{aligned} \int\int\frac{1}{2\pi}\exp\left(-\frac{1}{2}(u^2+v^2)\right)uv\mathrm{d}u\mathrm{d}v&=0\\ \int\int\frac{1}{2\pi}\exp\left(-\frac{1}{2}(u^2+v^2)\right)v^2\mathrm{d}u\mathrm{d}v&=1\\ \end{aligned}$

带入得到结果.

协方差矩阵

设随机变量$X=(X_1,\cdots,X_n)$,定义$E(X)=(E(X_1),\cdots,E(X_n))$为其数学期望向量,而$\mathrm{Cov}(X)=E((X-E(X))(X-E(X))^t)$为$X$的协方差矩阵.也就是$\mathrm{Cov}(X)_{i,j}=\mathrm{Cov}(X_i,X_j)$.容易见到其半正定,原因是$\alpha^t\mathrm{Cov}(X)\alpha=E((\alpha^t(X-E(X)))^2)$.

事实上应该总有$\mathrm{Cov}(AX)=A\mathrm{Cov}(X)A^t$,原因是:

$\mathrm{Cov}(AX)=E((AX-E[AX])(AX-E[AX])^t)$

Example1

求二维正态分布的协方差矩阵.

显然为:

$B=\begin{bmatrix} \sigma_1^2&\rho\sigma_1\sigma_2\\ \rho\sigma_1\sigma_2&\sigma_2^2 \end{bmatrix}$

此外$\det(B)=(1-\rho^2)\sigma_1^2\sigma_2^2$.其逆矩阵$B^{-1}=\frac{1}{1-\rho^2}\begin{bmatrix}\frac{1}{\sigma_1^2}&-\frac{\rho}{\sigma_1\sigma_2}\-\frac{\rho}{\sigma_1\sigma_2}&\frac{1}{\sigma_2^2}\end{bmatrix}$.

此时见到:

$\begin{aligned} f(x_1,x_2)&=\frac{\exp(-\frac{1}{2(1-\rho^2)}\left(\frac{(x_1-\mu_1)^2}{\sigma_1^2}+\frac{(x_2-\mu_2)^2}{\sigma_2^2}-\frac{2\rho(x_1-\mu_1)(x_2-\mu_2)}{\sigma_1\sigma_2}\right))}{2\pi \sigma_1\sigma_2\sqrt{1-\rho^2}}\\ &=\frac{1}{2\pi\sqrt {\det B}}\exp\left(-\frac{1}{2}(\vec x-\vec \mu)^TB^{-1}(\vec x-\vec \mu)\right) \end{aligned}$

从而容易推广到任意多维,只需定义:

$\begin{aligned} f(\vec x) &=\frac{1}{(2\pi)^{\frac{n}{2}}\sqrt {\det B}}\exp\left(-\frac{1}{2}(\vec x-\vec \mu)^TB^{-1}(\vec x-\vec \mu)\right) \end{aligned}$

Example2

求证:当$\vec X\sim N(\vec \mu,B)$,则$\vec Y=A\vec X+\vec b\sim N(A\vec \mu+\vec b,ABA^t)$,其中$A$必须行满秩.

当$A$是方阵的时候,直接可逆,于是:

$\begin{aligned} f_Y(y)&=f_X(A^{-1}(y-b))|\frac{\partial x}{\partial y}|\\ &=f_X(A^{-1}(y-b))|\frac{\partial y}{\partial x}|^{-1}\\ &=f_X(A^{-1}(y-b))|\frac{1}{\det A}|\\ &=\frac{1}{(2\pi)^{\frac{n}{2}}\sqrt {\det ABA^{t}}}\exp\left(-\frac{1}{2}(A^{-1}(\vec y-\vec b)-\vec \mu)^TB^{-1}(A^{-1}(\vec y-\vec b)-\vec \mu)\right)\\ &=\frac{1}{(2\pi)^{\frac{n}{2}}\sqrt {\det ABA^{t}}}\exp\left(-\frac{1}{2}(\vec y-A\vec \mu-\vec b)^T(ABA^{T})^{-1}(A^{-1}(\vec y-A\vec \mu-\vec b)\right) \end{aligned}$

此外,一般的多为高斯分布可以看作独立同分布标准正态分布线性变换后的结果,原因是当$X\sim N(0,I),Y\sim N(\vec \mu,B)$,当然有$Y=B^{\frac{1}{2}}X+\vec \mu$.

特别地,把一个有一定信息关系的东西$Y$变成$X$也只需要$X=B^{-\frac{1}{2}}(X-\vec \mu )$,这个过程一般叫白化.因为信息被缩简单了.

然而,考虑如果$X\sim N(0,I)$,如果$Y=AX$,此时$Y$的结果似乎只和$AA^t$有关,而与$A$竟然无关.特别地,如果$A$是一个正交矩阵,则$Y$干脆和$X$服从同样的分布.

这揭示了正态分布其实更关注于模长,换言之,当$\vec \mu=0,B=I$的时候,$f(\vec y)$其实是只和$\vec y$的模长相关的.此时如果看它的等密度轮廓线其实是一圈又一圈的圆.而拉伸之后就成了某种一圈又一圈的椭圆(因为要拉伸呀).

卷积

若$X,Y$相互独立,考虑$Z=X+Y$,则$f_Z(z)=\int_{-\infty}^{+\infty}f_X(z-y)f_Y(y)\mathrm{d}y$.

熵

离散情况下将熵定义为$H[X]=E(\log \frac{1}{P(X)})=\sum_{i}P_i\log \frac{1}{P_i}$.如果设$|X|=|\{x|P(x)>0\}|$,则容易见到$0\leq H[X]\leq \log|X|$.

接下来我们想定义条件熵,直观的理解是”去掉$X$的信息后$Y$还剩多少信息”:

$\begin{aligned} H[Y|X]&=\sum_xH[Y|X=x]P[X=x]\\ &=\sum_x\sum_yP(Y=y|X=x)P[X=x]\lg\frac{1}{P(Y=y|X=x)}\\ &=\sum_{x,y}P(Y=y,X=x)\lg\frac{1}{P(Y=y|X=x)}\\ &=E(\lg\frac{1}{P(Y|X)}) \end{aligned}$

首先检验$f(x)=x\ln x$是下凸函数,原因是$f’(x)=1+\ln x$而$f’’(x)=\frac{1}{x}>0$.于是琴生不等式给出$f(\frac{a+b}{2})\leq \frac{f(a)+f(b)}{2}$,或说$E(f(X))\geq f(E(X))$.

另外一个很重要的工具是对数求和不等式,对于任何非负实数$a_1,\cdots,a_n$和正数$b_1,\cdots,b_n$,记$a=\sum_i a_i,b=\sum_i b_i$,则:

$\sum_i a_i\log\frac{a_i}{b_i}\geq a\log \frac{a}{b}$

一个重要的性质是证明其是上凸函数,对于任意分布$P,Q$和$\lambda\in (0,1)$,都有:

$H[\lambda P+(1-\lambda)Q]\geq \lambda H[P]+(1-\lambda)H[Q]$

原因是考虑:

$f(\lambda p_i+(1-\lambda)q_i)\leq \lambda f(p_i)+(1-\lambda)f(q_i)$

可以见到以下性质:

$H[X,Y]=H[X]+H[Y|X]$.
$H[X|Y]\leq H[X]$.
作为(2)的推论,互信息$I(X,Y)=H[X]+H[Y]-H[X,Y]=H[X]-H[X|Y]\geq 0$.
对于一个确定性函数$g$,$H[X]\geq H[g(X)]$.
$I(X;YZ)=I(X;Z)+I(X;Y|Z)$.
$I(X;Y\mid Z)\leq I(X;Y)+H(Z)$.
当$X,Y,Z$满足Markov规则,或者说$P_{X,Y,Z}=P_XP_{Y|X}P_{Z|Y}$,或说$P_{Z|Y}=P_{Z|XY}$,则$I(X;Y)=I(X;Z)+I(X;Y|Z)$.这自然推出$I(X;Y)\geq I(X;Z)$,也即这个过程中信息不会增多.

(1)是上述的一个显然推论.

(2)的话考虑:

$\begin{aligned} &H[X]-H[X|Y]\\ =&\sum_x\left(P(X=x)\lg \frac{1}{P(X=x)}-\sum_y P(X=x,Y=y)\lg \frac{1}{P(X=x|Y=y)}\right)\\ =&\sum_x\left(\sum_y P(X=x,Y=y)\lg \frac{P(X=x|Y=y)}{P(X=x)}\right)\\ =&\sum_x\sum_y P(X=x,Y=y)\lg \frac{P(X=x,Y=y)}{P(X=x)P(Y=y)}\\ \end{aligned}$

不妨令$a_i=P(X=x,Y=y),b_i=P(X=x)P(Y=y)$.容易见到$a=\sum_i a_i=1,b=\sum_i b_i=1$.于是上式变为:

$\begin{aligned} &H[X]-H[X|Y]\\ =&\sum_i a_i\lg \frac{a_i}{b_i}\\ =&-\sum_i a_i\lg \frac{b_i}{a_i}\\ \geq &-\sum_i a_i (\frac{b_i}{a_i}-1)\\ =&-\sum_i (b_i-a_i)\\ =&0 \end{aligned}$

对于(4),轻易地:

$\begin{aligned} H[X,g(X)]&=H[g(X)]+H[X|g(X)]\\ H[X]&=H[g(X)]+H[X|g(X)] \end{aligned}$

然而后者非负,于是显然.特别地,当$g$是一个单射的时候,$H[X]=H[g(X)]$.

对于(5),留神到$H[X]=I(X;Z)+H[X|Z]$,考虑:

$\begin{aligned} I(X;YZ)&=H[X]-H[X|YZ]\\ &=I(X;Z)+H[X|Z]-H[X|YZ] \end{aligned}$

然而$I(X;Y\mid Z)=H[X| Z]-H[(X|Y)|Z]=H[X|Z]-H[X|YZ]$.

对于(6),考虑:

$\begin{aligned} I(X;YZ)&=I(X;Z)+I(X;Y\mid Z)\\ &=I(X;Y)+I(X;Z\mid Y)\\ I(X;Y\mid Z)&=I(X;Y)+I(X;Z\mid Y)-I(X;Z)\\ \end{aligned}$

然而$I(X;Z\mid Y)=H[Z|Y]-H[X|YZ]\leq H[Z]$,而$I(X;Z)\geq 0$,于是显然.

对于(7),考虑:

$\begin{aligned} I(X;YZ)&=I(X;Y)+I(X;Z\mid Y)\\ I(X;YZ)&=I(X;Z)+I(X;Y\mid Z)\\ \end{aligned}$

此外:

$\begin{aligned} I(X;Y)+I(X;Z\mid Y)&=H[X]-H[X|Y]+H[Z|Y]-H[Z|YX]\\ &=H[X]-H[X|Y]+H[Z|Y]-H[Z|Y]\\ &=I(X;Y) \end{aligned}$

于是$I(X;Z\mid Y)=0$,这就证毕.

KL散度

定义$D(P||Q)=\sum_x P(x)\lg \frac{P(x)}{Q(x)}$.其中如果$P(x)\ne 0$而$Q(x)=0$的情况出现,我们就说此时其为$+\infty$.我们想要证明:$D(P||Q)\geq 0$.考虑:

$\begin{aligned} D(P||Q)&=E_{x\sim Q}(\frac{P(X)}{Q(X)}\lg \frac{P(X)}{Q(X)})\\ &\geq f\left(E_{x\sim Q}(\frac{P(X)}{Q(X)})\right)\\ &=f(1)\\ &=0 \end{aligned}$

从而这的确是某种衡量偏离程度的算子.

此外还应当定义条件KL散度.考察:

$\begin{aligned} D(P_{X,Z}||Q_{X,Z})&=\sum_{(x,z)} P_{X,Z}(x,z)\log \frac{P_{X,Z}(x,z)}{Q_{X,Z}(x,z)}\\ &=\sum_{(x,z)} P_{Z|X}(z|x)P_{X}(x)\log \frac{P_{Z|X}(z|x)P_{X}(x)}{Q_{Z|X}(z|x)Q_{X}(x)}\\ &=D(P_X||Q_X)+\sum_{(x,z)} P_{Z|X}(z|x)P_{X}(x)\log \frac{P_{Z|X}(z|x)}{Q_{Z|X}(z|x)}\\ \end{aligned}$

将后面的部分定义为$D(P_{Y|X}||Q_{Y|X}\mid P_X)$.顺便应该有$D(P_{X,Z}||Q_{X,Z})\geq D(P_X||Q_X)$.

此外还应当证明KL散度凸性.对于概率分布对$(P_1,Q_1),(P_2,Q_2)$,以及任意$\theta\in [0,1]$,令$P=\theta P_1+(1-\theta)P_2,Q=\theta Q_1+(1-\theta)Q_2$.下面我们证明下凸:

$D(P||Q)\leq \theta D(P_1||Q_1)+(1-\theta)D(P_2||Q_2)$

此外,有趣的性质是证明$I(X;Y)=D(P_{XY}||P_XP_Y)$,不过这个只需简单转化即可.

另外,对任意$P_X,Q_X$和kernel$P_{Y|X}$,令$P_Y=P_X\circ P_{Y|X}$,$Q_Y=Q_X\circ P_{Y|X}$. 散度的data-processing不等式给出:$D(P_X||Q_X)\geq D(P_Y||Q_Y)$.

Example1

求证$d(p||q)=D(\mathrm{Bern}(p)||\mathrm{Bern}(q))\geq (2\log e)(p-q)^2$.

具体来说,$d(p||q)=p\log \frac{p}{q}+(1-p)\log \frac{1-p}{1-q }$.

编码

一般无损编码

考虑一个编码-解码过程,要求编码器Encode是一个到$\{0,1\}^*$的单射,从而存在其的一个左逆Decode满足$\text{Decode}(\text{Encode}(x))=x $.

对于编码,我们非常在意的是它的长度.考虑设$L(X)=\text{len}(\text{Encode}(X))$,我们下面将会估计$E(L(X))$的大小.

首先证明其下界,我们断言:

$H(X)-H(L)\leq E[L(X)]$

由于$H(X)-H(L)=H(X|L)$,因此其实只需要证明$H(X|L)\leq E[L]$.由于该编码无损,不妨设$n(l)$为满足$L(x)=l$的数量,容易见到$n(l)\leq 2^l$,立刻有$H(X|L=l)=\log_2 n(l)\leq l$.于是:

$H(X|L)=\sum_l P(L=l)H(X|L=l)\leq \sum_{l}P(L=l)l=E[L]$

此外我们还想要估计$H(L)$具体有多大,事实上:

$H(L)\leq \log_2(e(1+E[L]))$

下面来看一种比较优秀的编码方式.不妨假设$P(x_1)\geq P(x_2)\geq \cdots$,于是自然有$P(x_i)\geq \frac{1}{i}$.取码长$L(x_i)=\lfloor \log_2i\rfloor$.其实就是按照出现的频率用小码,则:

$\begin{aligned} E[L(X)]&=\sum_i P(x_i)\lfloor \log_2 i\rfloor\\ &\leq \sum_i P(x_i)\log_2 i\\ &\leq \sum_i P(x_i)\log_2 \frac{1}{P(x_i)}\\ &=H(X) \end{aligned}$

前缀码

一个更合适的例子是前缀码,对于一个$L(X)$函数,我们声称存在前缀码$f$使得$|f(x_i)|=L(x_i)$,当且仅当$\sum_{x\in A}2^{-L(x)}\leq 1$,原因是在二叉树上表示一下.

众所周知Huffman编码是最优编码,现在我们来看它为什么优秀,我们说其满足$H(X)\leq E[L(X)]\leq H(X)+1$,下面我们来证明这个结论.

先证上界,由于Huffman编码是最优编码,我们只要选取任意一个编码,使得它的界$\leq H(X)+1$即可.根据上面的引理,我们直接将$x$映射到一个长度为$\lceil \log \frac{1}{P(x)}\rceil$的前缀编码.此时:

$\begin{aligned} E(L(X))&=\sum_{x}P(x)\lceil \log \frac{1}{P(x)}\rceil\\ &\leq \sum_{x}P(x)\left(\log \frac{1}{P(x)}+1\right)\\ &=H(X)+1 \end{aligned}$

再来看下界.来证明任意前缀编码都会被这个下界控制住.

对于一个前缀编码,实际上是把$X$映射到了另一个$Y$处.由于这是一个单射,所以有$H(X)=H(Y)$.然而:

$\begin{aligned} H(Y)&=\sum_{t}H(Y_t|Y_{1}\cdots Y_{t-1})\\ \end{aligned}$

来看一个特定的$H(Y_t|Y_1\cdots Y_{t-1}=y_1\cdots y_{t-1})$,如果此时$y_1\cdots y_{t-1}$已经能解码了,那$Y_t$就一定是空白,因此此时熵为$0$;反之,则$Y_t$要么是$0$要么是$1$,伯努利分布的最大值只有$\log_2 2=1$.因此我们可以发现,对于一个特定的$x$和对应的$y_1\cdots y_k$,一定有$H(Y_t|Y_1\cdots Y_{t-1}=y_1\cdots y_{t-1})\leq Pr[L(x)\geq t]$.

所以实际上$H(Y)\leq \sum_t Pr[L(X)\geq t]=E(L)$.

几乎无损压缩

对于独立同分布$X^n$,如果满足:

$Pr[\text{Decode}(\text{Encode}(X^n))=X^n]\geq 1-\epsilon,\epsilon\to 0$

则称其为几乎无损压缩.不妨记录$\vec X\sim X^n$.

现在我们来看做到几乎无损压缩需要怎么办.我们将说明几乎就一定需要$nH(X)$左右的信息长度才足够.事实上:

$\forall \delta>0$,存在编码方案使得$L\leq n(H(X)+\delta)$,并且错误概率趋近于$0$.
$\forall \delta>0$,如果$L<n(H(X)-\delta)$,则无论怎么编码,错误概率趋近于$1$.

先来证明(1),考虑直接取$L=n(H(X)+\delta)$,并且编码出现概率最大的前$2^L$个元素,剩下的扔掉.不妨可以发现我们只会扔掉所有$P(\vec X)\leq 2^{-n(H(X)+\delta)}$的,原因是比这个阈值大的不可能超过$2^L$个.然而留意到$P(\vec X=(x_1,\cdots,x_n))=\prod_i P(X=x_i)$:

$\begin{aligned} Pr[P(\vec X)\leq 2^{-n(H(X)+\delta)}]&=Pr[-\log_2P(\vec X)\geq n(H(X)+\delta)]\\ &=Pr[-\sum_i\log_2P(X_i)\geq n(H(X)+\delta)]\\ \end{aligned}$

可是$\sum_i -\log_2 P(X_i)$的期望恰好为$H(X)$,因此根据Chernoff-Hoeffding Bound,这个错误概率$\leq e^{-O(n\delta^2)}$.

那么反过来的界怎么证明呢?此时最多可编码$2^{n(H(X)-\delta)}$个元素.仍然用Chernoff Bound就可以搞定了.

通用压缩

我们上面的所有讨论都基于已知分布的情况.如果我们不知道分布,又能做到多好的编码呢?

当编码的时候不知道分布,但解码的时候知道分布的时候,事实上可以做到:$\varlimsup_{n\to \infty}\frac{1}{n}E[L_n(X^n)]\leq H(X)+\epsilon$,其中$\epsilon$可以任意小.

这个怎么做呢?考虑一个暴力方法,我先随便将信息映射到$\{0,1\}^L$.此时的Encode并非单射.解码的时候直接最大似然估计找最好的那个解码.

假设$x_i\to c_i$,并且$P(x_1)\geq P(x_2)\geq \cdots$,取一个阈值$M=2^{n(H(X)+\delta)}$,以及$L=n(H(X)+2\delta)$现在来看失败概率也就是:

$\begin{aligned} &\sum_{i} P(x_i)Pr[c_i\in \{c_1,\cdots,c_{i-1}\}]\\ =&\sum_{i=1}^M P(x_i)Pr[c_i\in \{c_1,\cdots,c_{i-1}\}]+\sum_{i\geq M} P(x_i)Pr[c_i\in \{c_1,\cdots,c_{i-1}\}]\\ \leq &\sum_{i=1}^M P(x_i)\frac{M}{2^L}+2^{-O(n\delta^2)}\\ \leq &2^{-O(n\delta)}+2^{-O(n\delta^2)}\\ \end{aligned}$

这个错误概率就很小了.

信道编码

定义信道为某种会”污染”信息的东西,或者干脆写称条件概率分布$P_{Y|X}$.此外定义信道容量$C=\max_{P_X}I(X;Y)$,其中$(X,Y)\sim P_XP_{Y|X}$.

现在我们考虑一个一般的信道编码,取$W\to \vec X\in \mathcal{X}^L\to \vec Y\in \mathcal{Y}^L\to \hat W$.

现在我们来证明以下性质:

$I(\vec X;\vec Y)\leq L\sdot C$
data-processing不等式:$I(W;\hat W)\leq I(\vec X;\vec Y)$

对于(1),由于$Y_i$独立地依赖于$X_i$,考虑:

$\begin{aligned} I(\vec X;\vec Y)&=\sum_i I(\vec X;Y_i\mid Y_1\cdots Y_{i-1})\\ &=\sum_i I(X_i;Y_i)\\ &\leq L\sdot C \end{aligned}$

至于(2),实际上是互信息的data-processing不等式.

接下来我们要搞定传送速率的问题.不妨设$n=H(W)$,现在我们将要证明:

$n\leq\frac{LC+H(\epsilon)}{1-\epsilon}$

其中$\epsilon$是可接受的最大错误概率,定义为$\epsilon=\max_w Pr[\hat W\ne W|W=w]$.

怎么证明呢?考虑取一个指示变量$Z$,当$\hat W\ne W$的时候$Z=1$,否则$Z=0$.不妨直接让$Z$多错一点,到达$Pr[Z=1|W=w]\equiv \epsilon$以方便我们下面的分析.这样的话$Z$和$W$就独立了.此时立刻见到:

$(1-\epsilon)I(W;\hat W\mid Z=0)\leq I(W;\hat W\mid Z)\leq I(W;\hat W)+H(Z)$

而$I(W;\hat W\mid Z=0)=I(W;W)=H(W)=n$.

极限的情况

尾不等式

留神到如果事件在$n$次中发生了$n_a$次,其实是不能说$\lim_{n\to \infty}\frac{n_a}{n}=P$的.因为后面总是会有微小的扰动.但似乎总能刻画这些微小扰动的代价.

设$f_n(A)=\frac{n_a}{n}$.如果我们能求出$P(|f_n-p|\geq \epsilon)=P(|n_a-E(n_a)|\geq n\epsilon)$的上界,看上去就会非常优秀.进一步地:

尾不等式:给出$P(X\geq k)$的上界.
集中不等式:给出$P(|X-E(X)|\geq k)$的上界.

Example1

对二项分布用Chebyshev不等式,轻易有:

$P(|n_A-E(n_A)|\geq n\epsilon)\leq \frac{p(1-p)}{n\epsilon^2}$

这个估计有点菜,右侧是$O(\frac{1}{n})$的,这个趋近也太慢了.

考虑一下它为什么菜,问题在于Chebyshev不等式只用到了”两两独立”这件事,但是实际上二项分布更强一点,它其实是”互相独立”的.

矩

定义$E(X^k)$为$X$的$k$阶原点矩,而将$E((X-E(X))^k)$称为$X$的$k$阶中心距.则期望是其一阶原点矩而方差是二阶中心矩.

对于随机变量$X$,定义$M_X(t)=E(e^{tX})$为$X$的矩生成函数.考虑:

$\begin{aligned} E(e^{Xt})&=\sum_{k=0}^ne^{kt}P(X=k)\\ &=\sum_{k=0}^nP(X=k)\left(\sum_{j=0}^{+\infty}\frac{(kt)^j}{j!}\right)\\ &=\sum_{j=0}^{\infty}\frac{t^j}{j!}\sum_{k=0}^nP(X=k)k^j\\ &=\sum_{j=0}^\infty \frac{t^j}{j!}E(X^j) \end{aligned}$

Example2

对$X\sim B(n,p)$,求$E((X-E(X))^4)$.

考虑其矩生成函数:

$\begin{aligned} E(e^{Xt})&=\sum_{k=0}^ne^{kt}P(X=k)\\ &=\sum_{k=0}^ne^{kt}\binom{n}{k}p^k(1-p)^{n-k}\\ &=\sum_{k=0}^n\binom{n}{k}(pe^{t})^k(1-p)^{n-k}\\ &=(pe^t+(1-p))^n\\ &=(1+p(e^t-1))^n \end{aligned}$

令$Y=X-E(X)$,则$E(e^{Yt})=E(e^{Xt})e^{-tpn}$,现在我们可以对其求四次导数得到:

$E((X-E(X))^4)=np(1-p)^4+n(1-p)p^4+3n(n-1)p^2(1-p^2)$

那这个有什么用呢?考虑对其用Markov不等式:

$P((X-E(X))^4\geq (n\epsilon)^4)\leq \frac{O(n^2)}{(n\epsilon)^4}=O(\frac{1}{n^2\epsilon^4})$

这的确给出了一个更好的估计.

但是再做六阶矩好像也很痛苦,而且这只能给出一个多项式估计,但看着这个逼近速度就不太可能是多项式估计,那怎么办呢?

Chernoff Bound

考虑直接对$e^{tX}$用Markov不等式:

当$t>0$的时候,有$P(X\geq k)\leq M_X(t)e^{-tk}$.
当$t<0$的时候,有$P(X\leq k)\leq M_X(t)e^{-tk}$.

左侧没有$t$而右侧有,那看上去只要找到能使右侧取到最小值的$t$就万事大吉了.

Example1

当$X\sim \pi(\lambda)$的时候,求$P(X\geq x)$的上界.其中$x>\lambda$.

先求此时的矩生成函数:

$\begin{aligned} E(e^{Xt})&=e^{-\lambda}\sum_{k\geq 0}\frac{\lambda^k}{k!}e^{kt}\\ &=e^{-\lambda}\sum_{k\geq 0}\frac{(\lambda e^t)^k}{k!}\\ &=e^{\lambda (e^t-1)} \end{aligned}$

当$t>0$的时候,我们想要优化$e^{\lambda(e^t-1)-tx}$的最小值,直接对$t$求导,发现当$t=\ln\frac{x}{\lambda}$时最小.

此时:

$P(X\geq x)\leq \frac{e^{-\lambda}(e\lambda)^x}{x^x}$

Example2

当$X\sim N(\mu,\sigma^2)$,求$P(X-E(X)\geq k\sigma)$的上界.

还是求矩生成函数,考虑:

$E(e^{tX})=\int_{-\infty}^{+\infty}\frac{1}{\sqrt {2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}+tx}=e^{\mu t+\frac{\sigma^2t^2}{2}}$

从而:

$P(X\geq k\sigma+\mu)\leq e^{\mu t+\frac{\sigma^2t^2}{2}}e^{-t(\mu+k\sigma)}=e^{\frac{\sigma^2t^2}{2}-k\sigma t}$

当$t=\frac{k}{\sigma}$的时候取最小值,从而最后的界是$e^{-\frac{k^2}{2}}$.

Example3

当$X\sim B(n,p)$,求$P(X-E(X)\geq n\epsilon)$的上界.

考虑$M_X(t)=(1-p+pe^t)^n$.

然后需要一个Lemma,我们说$(1-p)e^{-tp}+pe^{t(1-p)}\leq e^{\frac{t^2}{8}}$,这个会在后面的Hoeffding引理证明.

直接带入,右侧为:

$\begin{aligned} M_X(t)e^{-t(E(X)+n\epsilon)}&=e^{-tn\epsilon}\left((1-p)e^{-tp}+pe^{t(1-p)}\right)^n\\ &\leq e^{-tn\epsilon+\frac{nt^2}{8}} \end{aligned}$

取$t=4\epsilon$得到$e^{-2n\epsilon^2}$的上界.

此外取$t=-4\epsilon$得到$P(X-E(X)\leq -n\epsilon)$的上界为$e^{-2n\epsilon^2}$.

于是我们有$P(|X-E(X)|\geq n\epsilon)\leq 2e^{-2n\epsilon^2}$.

Hoeffding引理

若实数随机变量$a\leq X\leq b$,则$M_{X-E(X)}(t)=E(e^{t(X-E(X))})\leq e^{\frac{t^2(b-a)^2}{8}}$.

Example1(Chernoff-Hoeffding不等式)

若$X=\sum_{i=1}^n X_i$,其中$X_i$相互独立且$a\leq X_i\leq b$.则($k> 0$):

$P(X\geq E(X)+k)\leq e^{-\frac{2k^2}{n(b-a)^2}}$.
$P(X\leq E(X)-k)\leq e^{-\frac{2k^2}{n(b-a)^2}}$.

怎么证明呢,考虑$P(X\geq E(X)+k)\leq M_{X-E(X)}(t)e^{-tk}$.

然而:

$\begin{aligned} M_{X-E(X)}(t)&=E(e^{t(X-E(X))})\\ &=E(\prod_i e^{t(X_i-E(X_i))})\\ &=\prod_i E(e^{t(X_i-E(X_i))})\\ &=\prod_i M_{X_i-E(X_i)}(t)\\ &\leq e^{n\frac{t^2(b-a)^2}{8}} \end{aligned}$

接下来对后面那个东西最优化,可以发现$t=\frac{4k}{n(b-a)^2}$的时候足够优秀,这就证明了上面的不等式.

Sanov Bound

回忆到斯特林公式$n!\sim \sqrt{2\pi n}(\frac{n}{e})^n$.

先来看一个在二项分布上的版本,不妨设$X_1,\cdots,X_n\sim \mathrm{Bern}(p)$,而$q>p$,我们断言:

$\frac{1}{n+1}\exp(-nd(q||p))\leq Pr[\sum_i^n X_i\geq qn]\leq (n(1-q)+1)\exp(-nd(q||p))$

为此留神到$Pr[\sum_i^n X_i\geq qn]=\sum_{t=qn}^n\binom{n}{t}p^t(1-p)^{n-t}$,容易证明当$q>p$的时候,$\binom{n}{t}p^t(1-p)^{n-t}$单调下降.

此时来看$\binom{n}{qn}$的取值:

$\begin{aligned} 1&\geq \binom{n}{qn}q^{qn}(1-q)^{n-qn}\\ \binom{n}{qn}&\leq \frac{1}{q^{qn}(1-q)^{n-qn}}\\ &=\left((\frac{1}{q})^q(\frac{1}{1-q})^{1-q}\right)^n\\ &=\left(\exp(q\ln \frac{1}{q}+(1-q)\ln \frac{1}{1-q})\right)^n\\ &=\exp(nh(q)) \end{aligned}$

此外,我们知道$\binom{n}{t}q^{t}(1-q)^{n-t}$在$t=qn$处取最大值,从而$ \binom{n}{qn}q^{qn}(1-q)^{n-qn}\geq \frac{1}{n+1}$,于是给出$\exp(nh(q))\geq \frac{1}{n+1}\exp(nh(q))$.

此时观察:

$\begin{aligned} \exp(nh(q))p^{qn}(1-p)^{n-qn}&=\exp(nh(q))\exp(n(q\ln p+(1-q)\ln (1-p)))\\ &=\exp(n(q\ln \frac{p}{q}+(1-q)\ln \frac{1-p}{1-q}))\\ &=\exp(-nd(q||p)) \end{aligned}$

从而给出了上面的答案.

现在来看一个一般的版本.对于一个可能的空间$\Omega=\{v_1,\cdots v_L\}$,现在有一个分布$P:\Omega\to [0,1]$,记录$p_i=P(v_i)$.

现在从$P$中独立取样$x_1,\cdots,x_n$.考虑对于一个特定的可重集合$S$,求$Pr[\{x_1,\cdots ,x_n\}=S]$.回忆到可重集的定义为$S:\Omega\to\mathbb{N}$,不妨干脆记录$s_i=S(v_i)$.容易发现$Pr[\{x_1,\cdots ,x_n\}=S]=\binom{n}{s_1,\cdots,s_L}p_1^{s_1}\cdots p_L^{s_L}$.

现在考虑一个新的分布$Q:\Omega\to [0,1]$,其中$q_i=\frac{s_i}{n}$,此时如果采样$y_1,\cdots,y_n\sim Q$的时候,先来看看$Pr[\{y_1,\cdots,y_n\}=S]$.

容易见到$|\Omega\to \mathbb N|\leq \frac{1}{(n+1)^{L-1}}$,从而见到以下简单估计(需要证明当前的情况的概率是所有情况中最大的):

$\begin{gathered} \frac{1}{(n+1)^{L-1}}\leq Pr[\{y_1,\cdots,y_n\}=S]\leq 1\\ \frac{1}{(n+1)^{L-1}}\leq \binom{n}{s_1,\cdots,s_L}\leq \left((\frac{1}{q_1})^{q_1}\cdots (\frac{1}{q_L})^{q_L}\right)^n\\ \frac{\exp(nH(Q))}{(n+1)^{L-1}}\leq \binom{n}{s_1,\cdots,s_L}\leq \exp(nH(Q))\\ \end{gathered}$

这给出了$\binom{n}{s_1,\cdots,s_L}$的一个上下界.然而天然有:

$p_1^{s_1}\cdots p_L^{s_L}=\exp(n\sum_i q_i\log p_i)=\exp(-nD(Q||P)-nH(Q))$

从而:

$\frac{\exp(-nD(Q||P))}{(n+1)^{L-1}}\leq Pr[\{x_1,\cdots ,x_n\}=S] \leq \exp(-nD(Q||P))\\$

如果这里把$\{x_1,\cdots ,x_n\}=S$弱化到$\{x_1,\cdots ,x_n\}\in A$,则右边当然要补一个$|A|$,当然显然$|A|\leq (n+1)^{L-1}$.也可以写:

$\frac{\max_{S\in A}\exp(-nD(Q_S||P))}{(n+1)^{L-1}}\leq Pr[\{x_1,\cdots ,x_n\}\in A] \leq |A|\max_{S\in A}\exp(-nD(Q_S||P))\\$

Example1

考虑$X_1,\cdots,X_n,Y_1,\cdots,Y_n$是$2n$个独立地随机变量.其中$X_i\sim \mathrm{Bern}(p),Y_i\sim \mathrm{Bern}(q)$,有$p>q$,求最小的不依赖于$n$的常数$c$使得:

$Pr[\sum_i^n X_i\leq \sum_i^n Y_i]\leq O(c^n)$

考虑令$Z_i=X_i-Y_i$,得知$P(Z_i=1)=p(1-q),P(Z_i=-1)=(1-p)q$.

现在考虑一个均匀一点的分布$W$满足$E(W)=0$.我们的目的是求出$\max_{E(W)=0}D(W||Z)$.

不妨设$P(W=1)=c\leq \frac{1}{2}$,则:

$\begin{align} D(W||Z)=c\log \frac{c}{p(1-q)}+c\log\frac{c}{q(1-p)}+(1-2c)\log\frac{1-2c}{1-p(1-q)-q(1-p)} \end{align}$

好吧我投降了,我们来带入数值吧,$p=\frac{4}{5},q=\frac{1}{2}$,于是:

$\begin{align} D(W||Z)&=2c\log (5c)+(1-2c)\log(2-4c)\\ \frac{\mathrm{d}D(W||Z)}{\mathrm{d}c}&=(2\log e)(\ln\frac{5c}{2-4c}) \end{align}$

所以$C=\frac{9}{10}$最优.

大数定律

对于随机变量$\{X_i\}$,对于任意$\epsilon>0$,如果:

$\lim_{n\to \infty} P(|\frac{1}{n}\sum_i^n X_i-\frac{1}{n}\sum_i^n E(X_i)|<\epsilon)=1$

则称它们满足大数定律.

一般而言,对于一列随机变量$\{Y_i\}$和一个随机变量$Y$,如果$\forall \epsilon>0$,$\lim_{n\to \infty}P(|Y_n-Y|<\epsilon)=1$,则称其依概率收敛.

Markov大数定律

若$\mathrm{Var}(\sum X_i)\sim o(n^2)$,则$\{X_n\}$符合大数定律.

策略是考虑$\mathrm{Var}(\frac{\sum X_i}{n})=\frac{1}{n^2}\mathrm{Var}(\sum X_i)$.用Chebyshev不等式碾一下就好了.

Khinchin大数定律(弱大数定律)

设$\{X_i\}$独立同分布,且数学期望$\mu=E(X_i)$存在,则$\{X_i\}$满足大数定律.

特征函数

对于随机变量$X$,设$\phi_X(t)=E(e^{itX})$为其特征函数.容易见到$\phi_X(-it)=E(e^{tX})$.一些常见的特征函数:

$X\sim \pi(\lambda),M_X(t)=e^{\lambda(e^t-1)},\phi_X(t)=e^{\lambda(e^{it}-1)}$.
$X\sim N(\mu,\sigma^2),M_X(t)=e^{\mu t+\frac{\sigma^2t^2}{2}},\phi_X(t)=e^{i\mu t-\frac{\sigma^2t^2}{2}}$.
$X\sim B(n,p),M_X(t)=(1-p+pe^t)^n,\phi_X(t)=(1-p+pe^{it})^n$.
$X$服从柯西分布,$f(x)=\frac{1}{\pi(x^2+1)}$,则$\phi_X(t)=e^{-|t|}$.

随机变量的分布函数由其特征函数唯一确定.此外,依分布收敛等价于特征函数逐点收敛.

依照上面的结论,就可以拿到$X_n\sim \pi(n)$推出$\frac{X_n-n}{\sqrt n}\to N(0,1)$,原因正是上面的依分布收敛的性质.

中心极限定理

先来看Lindeberg-Levy版本:

设$\{X_n\}$独立同分布,而且$E(X_n)=\mu,\mathrm{Var}(X_n)=\sigma^2$,设$Y_n=\sum_i^n X_i$,而$\tilde{Y}_n=\frac{Y_n-E(Y_n)}{\sigma(Y_n)}=\frac{\sum_i^n (X_i-\mu)}{\sqrt n\sigma}$.

我们断言$\tilde Y_n$一定依分布收敛于$Z$,其中$Z\sim N(0,1)$.

为什么呢?用泰勒展开考虑$\Re \phi_{X_n-\mu}(t)=1-\frac{\sigma^2}{2}t^2+o(t^2)$.此时$\Re \phi_{\tilde Y_n}(t)=(1-\frac{t^2}{2n}+o(\frac{t^2}{n}))^n\to e^{-\frac{t^2}{2}}$.

现在来看一个强的版本:

Berry-Esseen定理:在上述版本的基础上,如果$E(|X_n-\mu|^3)$有限,则收敛速度有:

$|P(\tilde Y_n\leq x)-P(Z\leq x)|\leq O(1)\frac{E(|X_n-\mu|^3)}{\sigma^3\sqrt{n}}$

概率方法

Example1

求证拉姆齐数$R(k,k)>2^{\frac{k-1}{2}}$.

考虑一个随机图,任何两个点之间以$\frac{1}{2}$概率连边,现在取点集的一个大小为$k$的子集,它是一个完全图或者或独立集的概率都是$2^{-\frac{k(k-1)}{2}}$,立刻见到这个图所有的期望大小为$k$的完全图或独立集的期望为$\binom{n}{k}2^{1-\frac{k(k-1)}{2}}$,如果这个东西$<1$,就证明总有一个图二者皆不存在.于是取$n=2^{\frac{k-1}{2}}$,则:

$\begin{aligned} \binom{n}{k}2^{1-\frac{k(k-1)}{2}}&< \frac{n^k}{k!}2^{1-\frac{k(k-1)}{2}}\\ &=\frac{2}{k!} \end{aligned}$

Example2

考虑一个大小为$n$的集合$X$的若干大小为$k$的子集所组成的集合$\Omega$,并且要求$\forall S,T\in \Omega,S\cap T\ne \emptyset$.求证:$|\Omega|\leq \binom{n-1}{k-1}$.

这个上界显然是容易达到的,只需要让所有子集都包含同一个元素即可.

现在考虑随机一个置换$\sigma$,选定$A_i=[i,k+i-1]$,考虑$Pr[\sigma(S)=A_i]=\frac{1}{\binom{n}{k}}$于是$Pr[\sigma(S)\in \{A_0,\cdots,A_{n-1}\}]=\frac{n}{\binom{n}{k}}$.从而$E(\sum_{S\in \Omega}[\sigma(S)\in \{A_0,\cdots,A_{n-1}\}])=\frac{n}{\binom{n}{k}}|\Omega|$.然而这个数必定小于等于$k$,因为置换不会改变相交性,而如果要从$\{A_0,\cdots,A_{n-1}\}$中选出若干个两两相交的,最多只能选出$k$个.

Example3

取若干个集合$A_1,\cdots,A_n$,$B_1,\cdots,B_n$,要求$|A_i|=k,|B_j|=l$,此外要求$A_i\cap B_i=\emptyset$,而且当$i\ne j$时,要求$A_i\cap B_j\ne\emptyset$.求证$n\leq \binom{k+l}{k}$.

考虑取$X=\bigcup_i(A_i\cup B_i)$,考虑在$X$上随机一个序关系,并设事件$E_i$为:$A_i$中的所有元素都$\leq $$B_i$中的所有元素.但这个事不能发生两次,因为如果$E_i$和$E_j$都成立,如果$A_i\cap B_j\ne \emptyset$,则$A_j\cap B_i=\emptyset$,这就完蛋了.所以$Pr[E_i]\leq \frac{1}{n}$.然而$Pr[E_i]=\frac{1}{\binom{l+k}{k}}$,这就搞定了.

Example4

求证$\forall k\geq 2$和$\forall n$,总存在矩阵$M\in \{0,1\}^{n\times n}$,使得:

$M$中$1$的数量约为$\Omega(n^{2-\frac{2}{k+1}})$.
不存在$k\times k$的全$1$子矩阵.

考虑每一位置按照$B(1,p)$随机,则全$1$的$k\times k$的子矩阵的期望个数为$p^{k^2}\binom{n}{k}^2$.对于这些问题,我们强行删它们中的一个$1$,在做完这些操作后,剩下的$1$的个数的期望就会$\geq pn^2-p^{k^2}\binom{n}{k}^2$,最终选定$p=(\frac{n^2}{k^2n^{2k}})^{\frac{1}{k^2-1}}$.

Example5

求证:对于$\forall k,l$,存在一个图,它的环的长度均$\geq l$,但它的最小染色数$\geq k$.

考虑一个两个点之间以$p$概率连边的随即图,存在一个长度为$i$的环的概率为$\frac{n^{\underline{i}}}{i}p^i\leq n^ip^i$.

考虑每个染色都是一个独立集,因此必定有$\chi(G)\alpha(G)\geq n$,其中$\chi(G)$是染色数,$\alpha(G)$是最大独立集大小.从而只需要让$\alpha(G)$足够小就行.

现在考虑$Pr[\alpha(G)\geq a]\geq \binom{n}{a}(1-p)^{\frac{a(a-1)}{2}}$.然后倒腾倒腾吧,取$p=n^{\frac{1}{2l}-1}$,懒得算了.

Example6

考虑一个有限集合$B\subseteq \mathbb{Z}\setminus\{0\}$,求证存在一个$A\subseteq B$,使得$|A|\geq \frac{|B|}{3}$,并且满足$\forall a_1,a_2\in A,a_1+a_2\notin A$.

假如我们在一个环上做这件事,比如$\mathbb{Z}_p$.当$B=\mathbb{Z}_p\setminus\{0\}$,其中$p=3k+2$的时候,此时可以选取$[k+1,2k+1]$中的元素,容易见到这占据了$\geq \frac{|B|}{3}$.而如果不然,我们可以随机一个$r$,使得$B\to \mathbb{Z}_p\setminus\{0\},b\mapsto br$.此时落在$[k+1,2k+1]$的期望就已经$\geq \frac{|B|}{3}$.$p$取足够大能包住$B$即可.

Example7

求证:存在一个竞赛图,其中的哈密顿路的数量$\geq \frac{n!}{2^{n-1}}$.

这个好像非常平凡,随机图上随机一个排列然后它是哈密顿路的概率就是$2^{n-1}$.

Example8

我们称竞赛图的$S_k$性质是,任何$k$个点组成的子集,都存在一个点赢过了这$k$个点.问是否总存在一个竞赛图满足$S_k$性质.

随机一个竞赛图,考虑其任何一个大小为$k$的子集.对于外面一个点$u$胜过了这$k$个点的概率是$2^{-k}$.外面一个点都没赢的概率是$(1-2^{-k})^{n-k}$.于是用Union Bound,存在一个问题的概率$\leq \binom{n}{k}(1-2^{-k})^{n-k}$.显然$n\to \infty$的时候这玩意趋近于$0$,所以肯定能找到满足条件的.

Example9

考虑一系列向量$\vec v_1,\cdots \vec v_n\in \{-1,1\}^l$,求证:

$\exists a_1,\cdots,a_n\in \{-1,1\}$,使得$\Vert\sum a_i\vec l_i\Vert^2\geq nl$.
$\exists a_1,\cdots,a_n\in \{-1,1\}$,使得$\Vert\sum a_i\vec l_i\Vert^2\leq nl$.

只要证明这玩意期望就是$nl$即可,随机$\{a_i\}$,容易见到$E(a_i)=0,E(a_i^2)=1,E(a_ia_j)=E(a_i)E(a_j)=0$.带进去算一下.

Example10

求证:随机一个$x\in[1,n]$,使得$P(|v(x)-\ln\ln n|>\lambda \sqrt{\ln\ln n})\leq \lambda^{-2}$.

拆贡献用Chebyshev不等式硬估,懒得抄过程了.

Example11

考虑一个随机图$G(n,m)$,也就是从$\frac{n(n-1)}{2}$中随机$m$条边留下.这上面可能有若干随着$m$单调的性质,比如连通性之类的.我们下面证明:对于一个单调性质$P$,存在一个函数$m^*(n)$,使得:

当$m(n)=\omega(m^*(n))$时,总有$\lim_{n\to \infty}Pr_{G\sim G(n,m(n))}(G\in P)=1$.
当$m(n)=o(m^*(n))$时,总有$\lim_{n\to \infty}Pr_{G\sim G(n,m(n))}(G\in P)=0$.

下面简单记$Pr_{G\sim G(n,m)}(G\in P)=Pr_{n,m}$.

现在考虑$Pr_{n,mk}$,显然我们可以随机$k$次,然后再把它们拼起来(虽然有重边,但是单调性质可以不管这个),从而$1-Pr_{n,mk}\leq (1-Pr_{n,m})^k$.

直接选取$m^(n)$为使得$Pr_{n,m^(n)}\geq \frac{1}{2}$的最小的解.则立刻就可以控制住.

不过,部分的单调性质有更强的性质,即$\forall \epsilon>0$,当$m(n)\geq(1+\epsilon)m^(n)$的时候就可以控制住,当$m(n)\leq (1-\epsilon)m^(n)$也可以控制住.甚至更强地,对于有的性质,这个$\epsilon$还可以换成$\epsilon(n)=o(1)$.

Example12

现在来看连通性的性质,假设以$\frac{\log n-\alpha(n)}{n}$的概率随机每条边,那么一个点成为孤点的概率就是$(1-\frac{\log n-\alpha(n)}{n})^{n-1}\approx \frac{1}{n}e^{\alpha(n)}$.从而孤立点个数(设为$W$)的期望就是$e^{\alpha(n)}$.

接下来算$\mathrm{Var}(W)$,拆开硬算算,得到$\mathrm{Var}(W)=e^{\alpha(n)}+O(1)$.

然而$W$非负,从而:

$\begin{aligned} Pr[W=0]&\leq Pr[|W-E|\geq E]\\ &\leq \frac{\mathrm{Var}(W)}{E^2(W)}\\ &\approx \frac{e^{\alpha(n)}+O(1)}{e^{2\alpha(n)}} \end{aligned}$

于是只要$\alpha(n)\to\infty$就完蛋了,这个图甚至会出现孤点.

现在假设以$\frac{\log n+\alpha(n)}{n}$的概率随机每条边,和上面一样,由于期望足够小,用Markov不等式,我们可以证明此时孤立点消失了.

然后需要把剩下的部分处理一下,存在一个大小为$k\in [2,\frac{n}{2}]$的块与外界不连通的概率是$\binom{n}{k}(1-p)^{k(n-k)}$,考虑$1-p\leq e^{-p}$和$\binom{n}{k}\leq (\frac{ne}{k})^k$,于是这个概率被$(\frac{ne}{k}e^{-p(n-k)})^k$限制住了.

当$k\in [2,\epsilon n]$的时候$n-k=O(n)$,从而这个概率立刻被限制住.反之当$k\in [\epsilon n,\frac{n}{2}]$的时候$k(n-k)=O(n^2)$,但是组合数被压到了$(\frac{e}{\epsilon})^{O(n)}$,这就足够跑赢了.

统计

点估计

将只依赖于样本,不依赖于任何位置参数的函数称作统计量.例如:

样本均值$\bar X=\frac{1}{n}\sum_{i=1}^n X_i$.
样本方差$S^2=\frac{1}{n-1}\sum_{i=1}^n(X_i-\bar X)^2$.
样本$k$阶矩$A_k=\frac{1}{n}\sum_{i=1}^n X_i^k$.
样本$k$阶中心矩$B_k=\frac{1}{n}\sum_{i=1}^n(X_i-\bar X)^k$.

对于$\theta$的估计量$\hat \theta$,定义偏差$\mathrm{Bias}(\hat \theta)=E(\hat \theta)-\theta$.如果其等于$0$,则称其是无偏的.如果$\lim_{n\to \infty}\mathrm{Bias}(\hat \theta)=\theta$,则称$\hat\theta$是渐进无偏的.

此外定义$\mathrm{MSE}(\hat \theta)=E\left((\hat\theta-\theta)^2\right)$.容易见到:

$\begin{aligned} \mathrm{MSE}(\hat\theta)&=E\left((\hat\theta-\theta)^2\right)\\ &=E\left((\hat\theta-E(\hat\theta)+E(\hat\theta)-\theta)^2\right)\\ &=E\left((\hat\theta-E(\hat\theta))^2\right)+\left(E(\hat\theta)-\theta\right)^2\\ &=\mathrm{Var}(\hat \theta)+\left(\mathrm{Bias}(\hat\theta)\right)^2 \end{aligned}$

因此对于无偏估计的$\mathrm{MSE}(\hat\theta)=\mathrm{Var}(\hat\theta)$.

此外,如果估计量依概率收敛,或言$\forall \epsilon>0$,$\lim_{n\to \infty}P\left(|\hat\theta_n-\theta|\geq \epsilon\right)=0$,则称$\hat\theta_n$是一致估计量.

我们有性质:如果$\lim_{n\to \infty}\mathrm{MSE}(\hat\theta_n)\to 0$,则$\hat\theta_n$为一致估计量.原因是:

$\begin{aligned} &P\left(|\hat\theta_n-\theta|\geq \epsilon\right)\\ =&P\left((\hat\theta_n-\theta)^2\geq \epsilon^2\right)\\ \leq &\frac{\mathrm{MSE}(\hat\theta_n)}{\epsilon^2} \end{aligned}$

Example1

假设$E(X)$和$\mathrm{Var}(X)$均存在,独立随机的样本序列$X_1,\cdots,X_n$,现在考虑$\hat\theta_A=\bar X$,$\hat \theta_B=X_1$.

显然它们都是$E(X)$的无偏估计.然而$\mathrm{MSE}(\hat\theta_A)=\frac{\mathrm{Var}(X)}{n}$,而$\mathrm{MSE}(\hat\theta_B)=\mathrm{Var}(X)$.

Example2

假设已知$X\sim U(0,\theta)$.考虑$\hat\theta_A=2\bar X$和$\hat\theta_B=\max_k\{X_k\}$.

容易见到$\hat\theta_A$无偏.现在来看$\hat\theta_B$,自然地:

$\begin{aligned} F_{\hat\theta_B}(x)&=(F_X(x))^n\\&=(\frac{x}{\theta})^n\\ E(\hat\theta_B)&=\int_0^{+\infty}(1-F_{\hat\theta_B}(x))\mathrm{d}x\\ &=\int_0^\theta(1-(\frac{x}{\theta})^n)\mathrm{d}x\\ &=\frac{n}{n+1}\theta \end{aligned}$

但至少$\hat\theta_C=\frac{n+1}{n}\hat\theta_B$无偏.

现在来看,容易见到$\mathrm{MSE}(\hat\theta)=\frac{\theta^2}{3n}$.留神到:

$\begin{aligned} E(\hat\theta_B^2)&=\int_0^{\theta^2}\left(1-\frac{x^{\frac{n}{2}}}{\theta^n}\right)\mathrm{d}x\\ &=\theta^2-\frac{2}{n+2}\theta^2\\ &=\frac{n}{n+2}\theta^2 \end{aligned}$

于是$\mathrm{Var}(\hat\theta_C^2)=(\frac{n+1}{n})^2\mathrm{Var}(\hat\theta_B^2)=\frac{\theta^2}{n(n+2)}$.

Example3

考虑$B_2$对$\mathrm{Var}(X)$的估计,显然有$B_2=\frac{1}{n}\sum_k X_k^2-(\bar X)^2$.也就是说$E(B_2)=E(X^2)-E(\bar X^2)$.看上去欣欣向荣,然而:

$\begin{aligned} E(\bar X^2)&=E((\bar X-E(\bar X)+E(\bar X))^2)\\ &=E((\bar X-E(\bar X))^2)+(E(\bar X))^2\\ &=(E(\bar X))^2+\frac{\mathrm{Var}(X)}{n} \end{aligned}$

这就出事了.

Example4(正态分布)

考虑估计一个正态分布$X\sim N(\mu,\sigma^2)$.取$\bar X$和$S^2$作为其期望和方差的估计量.现在我们将展示一个非常厉害的结论,那就是$\bar X$和$S^2$实际上是独立的.

考虑一个正交矩阵$U$,其第一行每个元素限定为$\frac{1}{\sqrt n}$,其余行任取.由于其正交性,这必然意味着其余行所有元素之和为$0$.现在来取$\vec Y=U\vec X$.从前的结论告知我们$\vec Y$服从$n$维高斯分布.而且:

$E(\vec Y)=(\sqrt n\mu,0,\cdots,0)$.
$\mathrm{Cov}(\vec Y)=\sigma^2I$.
$\sum_k Y_k^2=\sum_k X_k^2$.

其中(1)是由于除第一行外,每一行的所有元素和为$0$.(2)是因为原本的$\vec X$的各个分量独立.(3)是因为正交变换保模长.

此时必定有$\bar X=\frac{Y_1}{\sqrt n}$,事实上还有:

$\begin{aligned} (n-1)S^2&=\sum_{i=1}^n(X_i-\bar X)^2\\ &=(\sum_k X_k^2)-n\bar X^2\\ &=\sum_{k=1}^nY_k^2-Y_1^2\\ &=\sum_{k=2}^nY_k^2 \end{aligned}$

于是二者独立.还能得知$\bar X\sim N(\mu,\frac{\sigma^2}{n})$,以及$\frac{(n-1)S^2}{\sigma^2}\sim\chi^2(n-1)$.

矩法

显然$k$阶矩的估计总是无偏的.因此一个想法是将我们想要估计的量写成矩的函数,再分别估计矩(注意,这样做在该函数并非一次的时候当然未必无偏).

最大似然估计

尝试选择参数$\theta$,使得$L(\theta)=P(X_1=x_1,\cdots,X_n=x_n|\theta)$最大.

如果样本干脆是均匀随机的,那就只需要最大化对数似然函数$\ln L(\theta)=\sum_{i=1}^n \ln P(X_i=x_i|\theta)$.

这样做当然不可能是无偏的.

Example1

考虑一个均匀分布$U(0,\theta)$,对其进行最大似然估计的结果是$\hat\theta=\max\{x_1,\cdots,x_n\}$.

Example2

考虑一个分类函数$f:X\to Y$.现在我们已经有其采样的一些结果$(x_i,y_i)$,想要去估计一个函数$f_\theta$.根据上面说的,我们需要最小化$\sum_{i=1}^n-\ln f_\theta(y_i|x_i)$.

现在考虑一个标签分布$g(y|x_i)=[y=y_i]$.我们来看交叉熵:

$\begin{aligned} H(g,f_\theta)&=-\sum_{y}g(y|x_i)\ln f_\theta(y|x_i)\\ &=-\ln f_\theta(y_i|x_i) \end{aligned}$

区间估计

我们想要更进一步,对于一个想要估计量$\theta$,以及两个统计量$\hat\theta_L$和$\hat\theta_R$,如果必有$P(\hat\theta_L\leq \theta\leq \hat\theta_U)\geq 1-\alpha$,则称$[\hat\theta_L,\hat\theta_R]$为$\theta$的置信水平为$1-\alpha$的置信区间.类似还可以定义单侧置信下限和单侧置信上限.

Example1

对于一个$X\sim N(\mu,\sigma^2)$,假设$\sigma^2$已知,设计一个对$\mu$的置信水平为$1-\alpha$的估计.

考虑$\bar X\sim N(\mu,\frac{\sigma^2}{n})$.此时必定有$\frac{\bar X-\mu}{\frac{\sigma}{\sqrt{n}}}\sim N(0,1)$.只需要取一组$c,d$,使得$P(c\leq \frac{\bar X-\mu}{\frac{\sigma}{\sqrt{n}}}\leq d)=1-\alpha$即可.

现在取$\Phi(x)=\int_{-\infty}^x\frac{1}{\sqrt{2\pi}}e^{-\frac{t^2}{2}}\mathrm{d}t$为其分布函数,取$c=\Phi^{-1}(\frac{\alpha}{2}),d=\Phi^{-1}(1-\frac{\alpha}{2})$.留神到$c+d=0$.化简就有:

$P(\bar X-\frac{\Phi^{-1}(1-\frac{\alpha}{2})\sigma}{\sqrt n}\leq \mu\leq \bar X+\frac{\Phi^{-1}(1-\frac{\alpha}{2})\sigma}{\sqrt n})=1-\alpha$

不过这个估计因为要算$\Phi^{-1}$,可能意义不是特别大.回忆到Chernoff Bound给出:

$P(X-E(X)\geq k\sigma)\leq e^{-\frac{k^2}{2}}$

于是立刻有$P(|\bar X-\mu|\geq \frac{k\sigma}{\sqrt n})\leq 2e^{-\frac{k^2}{2}}$.

从而:

$P(\bar X-\frac{\sigma\sqrt{2\ln(\frac{2}{\alpha})}}{\sqrt n}\leq \mu\leq \bar X+\frac{\sigma\sqrt{2\ln(\frac{2}{\alpha})}}{\sqrt n})\geq 1-\alpha$

现在我们来干另一件事,众所周知,中心极限定理说大部分估计最后都会趋于一个正态分布.那么在此时,能否估计出$P(\mu=\bar X)=O(\frac{1}{\sqrt n})$呢?

考虑取$\alpha=1-O(\frac{1}{\sqrt n})$,就可以发现这个时候的$\mu$已经落在$\bar X\pm O(1)$的区间内了.

Example2

考虑对$X\sim B(1,p)$.设计$p$的置信水平$1-\alpha$的置信区间.

直接考虑Chernoff Bound,给出$P(|\bar X-p|>\epsilon)\leq 2e^{-2n\epsilon^2}$.取$\epsilon=\sqrt{\frac{\ln\frac{2}{\alpha}}{2n}}$,于是:

$P(\bar X-\sqrt{\frac{\ln(\frac{2}{\alpha})}{2n}}\leq p\leq \bar X+\sqrt{\frac{\ln(\frac{2}{\alpha})}{2n}})\geq 1-\alpha$

回归分析

考虑一个随机取样,满足$y=\alpha+\beta x+\epsilon$,其中$\epsilon$是随机误差,满足$E(\epsilon)=0,\mathrm{Var}(\epsilon)=\sigma^2<\infty$,而且若干次取样的误差互相独立.

我们的目标是给定数据$(x_1,y_1),(x_2,y_2),\cdots,(x_n,y_n)$,去估计出$\hat \alpha$和$\hat \beta$.这里有若干种估计策略:

最小二乘估计

一元

最小化$Q(\alpha,\beta)=\sum_i^n(y_i-\beta x_i-\alpha)^2$.

最简单的最优化方式当然是直接求偏导,留神到:

$\begin{align} \frac{\partial Q}{\partial \beta}&=-2\sum_i x_i(y_i-\beta x_i-\alpha)\\ \frac{\partial Q}{\partial \alpha}&=-2\sum_i(y_i-\beta x_i-\alpha) \end{align}$

让上述均为$0$,可以解出:

$\begin{align} \hat\beta &=\frac{\sum x_i y_i-\frac{1}{n}(\sum x_i)(\sum y_i)}{\sum x_i^2-\frac{1}{n}(\sum x_i)^2}\\ \hat \alpha &=\frac{1}{n}\sum y_i-\hat \beta \frac{1}{n}\sum x_i \end{align}$

如果我们为了方便,记$s_{xx}=\sum (x_i-\bar x)(x_i-\bar x)$以及$s_{xy}=\sum (x_i-\bar x)(y_i-\bar y)$,则:

$\begin{align} \hat\beta &=\frac{s_{xy}}{s_{xx}}\\ \hat \alpha &=\bar y-\hat \beta \bar x \end{align}$

现在来看这个估计有多准,容易见到:

$\begin{align} s_{xy}&=\sum(x_i-\bar x)(y_i-\bar y)\\ &=\sum(x_i-\bar x)(\alpha+\beta x_i+\epsilon_i-\bar y)\\ &=\sum (x_i-\bar x)(\beta x_i+\epsilon_i)\\ s_{xx}&=\sum(x_i-\bar x)(x_i-\bar x)\\ &=\sum x_i(x_i-\bar x) \end{align}$

从而见到:

$\begin{align} \hat \beta&=\frac{s_{xy}}{s_{xx}}\\ &=\beta+\frac{\sum (x_i-\bar x)\epsilon_i}{s_{xx}}\\ \hat \alpha&=\bar y-\hat \beta \bar x\\ &=\frac{\sum (\alpha+(\beta -\hat \beta)x_i+\epsilon_i)}{n}\\ &=\alpha+\frac{1}{n}(\sum \epsilon_i-\frac{(\sum x_i)(\sum(x_i-\bar x)\epsilon_i)}{s_{xx}})\\ &=\alpha+\sum \epsilon_i(\frac{1}{n}-\frac{(x_i-\bar x)\bar x}{s_{xx}}) \end{align}$

容易见到如果$E(\epsilon_i)=0$,那上述两个估计都是无偏的.现在来看他们的方差吧.

$\begin{align} \mathrm{MSE}(\hat\beta)=\mathrm{Var}(\hat\beta)&=\sum \mathrm{Var}(\epsilon_i)(\frac{x_i-\bar x}{s_{xx}})^2\\ &=\frac{\sigma^2}{s_{xx}}\\ \mathrm{MSE}(\hat \alpha)=\mathrm{Var}(\hat \alpha)&=\sigma^2\sum\left(\frac{1}{n}-\frac{(x_i-\bar x)\bar x}{s_{xx}}\right)^2\\ &=\sigma^2\sum\left(\frac{1}{n^2}-\frac{2}{n}\frac{(x_i-\bar x)\bar x}{s_{xx}}+(\frac{(x_i-\bar x)\bar x}{s_{xx}})^2\right)\\ &=\sigma^2\left(\frac{1}{n}+\frac{\bar x^2}{s_{xx}}\right) \end{align}$

而它们的协方差:

$\begin{align} \mathrm{Cov}(\hat\alpha,\hat\beta)&=E\left(\sum \epsilon_i^2(\frac{1}{n}-\frac{(x_i-\bar x)\bar x}{s_{xx}})(\frac{ (x_i-\bar x)}{s_{xx}})\right)\\ &=E\left(\sum_i \epsilon_i^2\frac{1}{n}\frac{x_i-\bar x}{s_{xx}}\right)-E\left(\sum_i \epsilon_i^2\bar x(\frac{x_i-\bar x}{s_{xx}})^2\right)\\ &=\sum_i \frac{1}{n}\frac{x_i-\bar x}{s_{xx}}\sigma^2-\sum_i \sigma^2\bar x(\frac{x_i-\bar x}{s_{xx}})^2\\ &=-\sigma^2\frac{\bar x}{s_{xx}} \end{align}$

于是我们现在可以估计$\hat y_i=\hat \alpha+\hat\beta x_i$的情况,容易见到$E(\hat y_i)=y_i$,但是:

$\begin{align} \mathrm{Var}(\hat y_i)&=\mathrm{Var}(\hat \alpha+\hat\beta x_i)\\ &=\mathrm{Var}(\hat \alpha)+x_i^2\mathrm{Var}(\hat\beta)+2x_i\mathrm{Cov}(\hat \alpha,\hat \beta)\\ &=\sigma^2\left(\frac{1}{n}+\frac{\bar x^2}{s_{xx}}\right)+x_i^2\frac{\sigma^2}{s_{xx}}-2x_i\sigma^2\frac{\bar x}{s_{xx}}\\ &=\sigma^2\left(\frac{1}{n}+\frac{(\bar x-x_i)^2}{s_{xx}}\right) \end{align}$

现在来看:

$\begin{align} \mathrm{Var}(\hat y_i-y_i)&=\mathrm{Var}(\hat y_i)+\mathrm{Var}(y_i)-2\mathrm{Cov}(\hat y_i,y_i)\\ &=\mathrm{Var}(\hat y_i)+\mathrm{Var}(y_i)-2\mathrm{Cov}(\hat \alpha+\hat\beta x_i,\alpha+\beta x_i+\epsilon_i)\\ &=\mathrm{Var}(\hat y_i)+ \sigma^2-2\mathrm{Cov}(\hat \alpha+\hat\beta x_i,\epsilon_i)\\ &=\sigma^2\left(\frac{1}{n}+\frac{(\bar x-x_i)^2}{s_{xx}}\right)+\sigma^2-2\sigma^2(\frac{1}{n}-\frac{(x_i-\bar x)\bar x}{s_{xx}})-2\sigma^2\frac{x_i-\bar x}{s_{xx}}x_i\\ &=\frac{n-1}{n}\sigma^2-\frac{(\bar x-x_i)^2}{s_{xx}}\sigma^2 \end{align}$

从而:

$\begin{align} E(\sum (\hat y_i-y_i)^2)&=\sum \mathrm{Var}(\hat y_i-y_i)\\ &=(n-1)\sigma^2-\frac{s_{xx}}{s_{xx}}\sigma^2\\ &=(n-2)\sigma^2 \end{align}$

总结一下我们上面做的事情,我们搞定了:

$\hat \alpha$和$\hat \beta$是$\alpha$和$\beta$的无偏估计.
$s^2=\frac{1}{n-2}\sum (\hat y_i-y_i)^2$是$\sigma^2$的无偏估计.

此外,简单验证可以说明当$\epsilon_i\sim N(0,\sigma^2)$时,最小二乘估计出的$\hat \alpha$和$\hat \beta$就是最大似然估计,而且因为它们都是$\epsilon_i$的线性组合,它们实际上是一个二维高斯分布.

多元

考虑一个$y=\beta_0+\cdots +\beta_k x_k+\epsilon$,其中$E(\epsilon)=0,\mathrm{Var}(\epsilon)=\sigma^2$,并且每次独立误差.

现在考虑能否用若干组数据去估计$\hat \beta_0,\cdots,\hat \beta_k$.

造$\vec x_i=[1,x_{i,1},\cdots,x_{i,k}]^t\in \mathbb{R}^{k+1}$,以及$\vec \beta=[\beta_0,\cdots,\beta_k]\in \mathbb{R}^{k+1}$.并设$X\in \mathbb{R}^{n\times (k+1)}$,其中$X^t=[\vec x_1,\cdots,\vec x_n]$,也就是说$X$第$i$行是$\vec x_i^t$.当然有$\vec y=X\vec\beta+\vec \epsilon$,此外$E(\vec y)=X\vec \beta$,$\mathrm{Cov}(\vec y)=\sigma^2 I_n$.

现在我们仍然用最小二乘估计,设$Q(\vec \beta)=\sum_i (y_i-\vec x_i^t\vec \beta)^2=|\vec y-X\vec \beta|^2$.

来看一下如何让这个东西最小,lww告诉我们需要让$X\vec \beta$正好打向$\vec y$向$\mathrm{im} X$的投影.回忆到$(\mathrm{im}X)^\bot=\ker X^t$,于是只需要$X^tX\vec\beta=X^t\vec y$即可.

当$X$列满秩的时候,根据奇异值分解有$X^tX$可逆,这个时候就有$\hat \beta=(X^tX)^{-1}X^t(X\vec \beta+\vec \epsilon)=\vec \beta+(X^tX)^{-1}X^t\vec \epsilon$,从而必然有$E(\hat \beta)=\vec \beta$.此外回忆到$\mathrm{Cov}(AX)=A\mathrm{Cov}(X)A^t$,于是:

$\begin{align} \mathrm{Cov}(\hat \beta)&=\sigma^2(X^tX)^{-1}X^t((X^tX)^{-1}X^t)^t\\ &=\sigma^2(X^tX)^{-1}X^tX(X^tX)^{-1}\\ &=\sigma^2(X^tX)^{-1} \end{align}$

另外,我们的估计是$\hat y=X\hat \beta=X(X^tX)^{-1}X^t\vec y$,下面我们设$H=X(X^tX)^{-1}X^t$,这个矩阵看上去性质就很好.它事实上显然有如下的性质:

$\mathrm{trace}(H)=k+1$.
$H^2=H$.
$H^t=H$.
$H$的特征值只有$1$和$0$.
$H$半正定.
$HX=X$.
$(I-H)^2=I-H$.

那么就有:

$\begin{align} \hat y-\vec y&=(H-I)\vec y\\ &=(H-I)(X\vec \beta+\vec \epsilon)\\ &=(H-I)\vec \epsilon\\ \mathrm{Cov}(\hat y-\vec y)&=\sigma^2(H-I)^2\\&=\sigma^2(I-H)\\ E(|\hat y-\vec y|^2)&=\mathrm{trace}(\mathrm{Cov}(\hat y-\vec y))\\ &=\sigma^2\mathrm{trace}(I-H)\\ &=\sigma^2(n-k-1) \end{align}$

这就给出了$s^2=\frac{1}{n-k-1}|\hat y-\vec y|^2$是$\sigma^2$的无偏估计量.

这个估计有多准呢?来看$\epsilon_i\sim N(0,\sigma^2)$的情况,此时回忆到$\hat \beta=\vec \beta+(X^tX)^{-1}X^t\vec \epsilon$服从一个多维高斯分布$N(\vec \beta,\sigma^2(X^tX)^{-1})$.考虑正交对角化给出$I-H=Q^t\Lambda Q$,由于旋转不变性,$\frac{(I-H)\vec \epsilon}{\sigma}$实际上就是$n-k-1$个独立同分布服从标准正态分布的随机变量,于是$\frac{|\hat y-\vec y|^2}{\sigma^2}\sim \chi^2(n-k-1)$.顺便一提,这里可以看出$s^2$和$\hat \beta$实际上依赖的东西是正交的.它们事实上互相独立.

最后,当我们拿到一个新的向量$\vec x_0$的时候,观察此时的估计值$\vec y_0=\vec x_0^t\hat \beta$,显然有$E(\vec x_0^t\hat \beta)=\vec x_0^t\vec \beta$以及$\mathrm{Cov}(\vec x_0^t\hat \beta)=\sigma^2\vec x_0^t(X^tX)^{-1}\vec x_0$.

不过上面这些分析都没太给出定性的结果.现在让我们来看$r^2=1-\frac{\sum(y_i-\hat y_i)^2}{\sum(y_i-\bar y)^2}=\frac{\sum(\hat y_i-\bar y)^2}{\sum (y_i-\bar y)^2}$.它实际上解释了总平方和中,回归平方和所占的比例.

岭回归

考虑最小化$Q_\lambda(\vec \beta)=\sum (y_i-\vec x_i^t\vec \beta)^2+\lambda |\vec \beta|^2$.

TODO

Lasso回归

最小化$Q_\lambda(\vec \beta)=\sum (y_i-\vec x_i^t\vec \beta)^2+\lambda \Vert\vec \beta\Vert_1$.

数论相关

发表于 2025-06-23 更新于 2025-08-15 分类于具体数学 Waline：

Here's something encrypted, password is required to continue reading.

阅读全文 »

数据结构相关

发表于 2025-06-23 分类于 OI Waline：

数据结构理论

维度

B维正交范围

对于一个$B$维的点$x$,满足$\forall 1 \leq i \leq B , l_i \leq x_i \leq r_i$,称所有这样的点组成的集合为一个$B$维正交范围.

一维正交范围就是区间,二维正交范围是矩形,三维正交范围是立方体.

另外,如果$l , r$有若干个是自动满足的(所有点都满足),那么我们称它为无用限制,如果一个$B$维正交范围有$k$个有用限制,称它为$k - side$的.

例如,找到区间$[ l , r ]$中$< x$的元素,这个矩形是$3 - side$的.找到区间$[ 1 , l ]$中$< x$的元素,这个矩形是$2 - side$的.有些矩形虽然是高side的,但可能因为某些维度满足可减性,因此可能等价于一个低side的问题.

(lxl:我建议大家遇到题都要把能差分的东西差分到不能差分为止)

矩阵乘法归约

矩阵乘法

做$n \times n$的矩阵乘法目前得到的最优秀复杂度也是$O ( n^{ 2 . 373 } )$.

另外可以归约:$01$矩阵和整数矩阵在去除$\log n$后的复杂度相同.

Example

Example1(链颜色数问题)

考虑构造一棵树:他有$\sqrt{ n }$个叉,每个叉上有$\sqrt{ n }$个点.我们将这些叉编号为$[ 1 , \sqrt{ n } ]$.然后我们考虑询问两个叉所组成的链的答案,设$f_{ i , j }$表示数字$j$是否在$i$的叉上出现过,不难发现它们合并的时候要对$f$做或运算,$01$矩阵乘法相当于且运算,显然这两个运算等价,证毕.

Example2(区间逆序对)

考虑对序列和值域同时分块,考虑序列中第$L$到第$R$个块的答案,设为$f ( L , R )$,这两块间的答案设为$g ( L , R )$,显然$f ( L , R ) = f ( L + 1 , R ) + f ( L , R - 1 ) - f ( L + 1 , R - 1 ) + g ( L , R )$,而由于对值域分块,$g ( L , R ) = \sum a \times b$的形式.根据这个形式构造即可.当然这个只是简化了好多,你会发现这个东西只能处理矩阵某一行递增的情况.lxl:真正的归约是很复杂的.

Example3

平面上有若干点,两个操作:每次将横坐标小于等于$A$的点加上$v$,或者查询纵坐标小于等于$B$的点的点权和.

这玩意显然能加上扫描线归约区间逆序对.

数据结构

分块

Example1(luoguP8527 [Ynoi2003] 樋口円香)

首先将$a$分块,这样对于一次修改就分成了整块和散块.散块暴力做,整块的话显然是一个位移的形式,可以直接卷积,比较简单.

不过我们先考虑个事:这么顺溜就出来了,为啥会需要分块啊?

首先看到题面的位移的形式,自然想到卷积.但问题在于有个区间,所以需要把区间处理掉.注意到每个区间是需要记录一下不同的$L$的,这使得这个问题只能使用分块解决.

最后还没完,这题要平衡复杂度.

设块长为$B$,暴力处理散块的复杂度是$O ( Bm )$,处理整块的复杂度是$O ( \frac{ n }{ B } ( m + n \log n ) )$.取$B^2 = \frac{ n }{ m } ( m + n \log n ) = 500$最优.

但事实上FFT肯定是很慢的,所以我开到了$B = 2048$.

即使这样,笔者还是被卡常了(哭).

Example2(luogu[Ynoi2079] riapq)

首先对于这种区间内部贡献,而且每个点由前面点的贡献,先看有没有可差分性(区间逆序对也是一个套路).

注意到是有的,这样我们就把问题转化为了$[ 1 , l - 1 ]$对$[ l , r ]$的贡献.

先序列分块.然后$[ 1 , l - 1 ]$中的整块对$[ l , r ]$的贡献是简单的:我们对每个整块开一个区间加单点查的树状数组,每次将$[ 1 , l - 1 ]$中的整块的树状数组进行一个$[ l , r ]$的区间加,查询的时候查一下每个整块对当前单点的贡献,这里需要对整块内部提前处理一下小于等于某个数的数量,自然可以做到$O ( Bq \log n )$的时间复杂度和$O ( Bn )$的空间复杂度.

问题在于$[ 1 , l - 1 ]$中的散块咋办.首先$[ 1 , l - 1 ]$中的散块对$[ l , r ]$中的散块的贡献是好处理的,因为总共就$O ( \frac{ n }{ B } )$个数字,直接全部存下来排序做归并就可以统计,时间复杂度$O ( Bq \log n )$.

现在的问题在于$[ 1 , l - 1 ]$中的散块对$[ l , r ]$中的整块如何贡献.能不能把$[ l , r ]$的信息统计在$[ 1 , l - 1 ]$的散块中呢?似乎不太行.因为散块的总数太多了.所以我们考虑把散块的信息记录在整块里.但是好像不太好记,因为你查询一个整块内的点的时候是需要判断记录的这些信息是否比它要小的,只有比它小的才能贡献.自然想到值域分块.不过还有一个问题,就是散块一共有$\frac{ n }{ B }$个,整块一共有$B$个,是不能一一对应着贡献的,这咋办呢?

其实挺好办的,因为散块要对一个区间有贡献,所以拿树状数组+差分统计一下就行.

最终复杂度为$O ( n \sqrt{ n } \log n )$,需要进行一个极致卡常.

如果你写完代码测一下会发现,跑的最慢的是散块对散块的贡献,你把sort改成基数排序就行.事实上实测了一下基数排序还不如直接换成树状数组.

但即使这样,笔者现在也没过这个题(哭).

Example3([CTS2022] 普罗霍洛夫卡)

比较复杂的分块题.

放弃了,太难了.

Example4(Walking Plan HDU 6331)

类似BSGS一样分块处理即可,最后需要枚举中继点,询问部分复杂度$O ( nq )$.

Example5(P5063 [Ynoi2014] 置身天上之森)

考虑如果$n = 2^k$,很好做,因为每一层的点大小是相等的.我们对每一层分开处理,显然区间加操作也就等价于每一层的节点区间加上若干倍的$a$(开头结尾可能有两个需要特殊判断),用分块求区间rank的技巧就行.

但是$n$不一定是$2^k$,也简单,每一层最多有两种不一样大小的点,这是经典结论.

Example6(第二分块:[Ynoi2018]五彩斑斓的世界)

大概是对于每个块处理出它的值域范围:一开始是$[ 1 , n ]$,然后每次操作都会将整个块分为两部分:$[ 1 , x )$和$[ x , maxn ]$,讨论一下$maxn$和$2 x$的大小,就可以用$\min ( x , maxn - x )$的复杂度使得$maxn$变成$maxn - x$,复杂度均摊掉了.

二次离线

Example1(luoguP5047 [Ynoi2019 模拟赛] Yuno loves sqrt technology II)

简单来说就是区间逆序对数.

首先想到莫队,然后配一个树状数组就可以做到$O ( n \sqrt{ n } \log n )$.

那我们怎么改这个东西呢?

我们注意到:我们莫队在实现的无非是俩事:一个是移动左端点的时候判断左端点对右边的贡献,一个是移动右端点的时候,由于这俩是对称的,我们只讨论左端点不动移动右端点.

考虑这个过程的答案实际上是可差分的,因为$[ l , r ]$对$r$的贡献实际上就是$[ 1 , r ]$对$r$的贡献减去$[ 1 , l - 1 ]$对$r$的贡献,前者可以直接算,而后者呢?

我们考虑对后者再进行一次离线操作,我们把这$O ( n \sqrt{ n } )$次贡献查询全都记下来,然后扫描线处理一下.注意到我们只需要插入$O ( n )$次但是需要查询$O ( n \sqrt{ n } )$次,所以需要使用一下值域分块平衡一下复杂度.

做到这里其实要做完了,但还没完,这里空间复杂度达到了$O ( n \sqrt{ n } )$,有点大.咋办呢?我们发现右端点移动的时候左端点不动,并且右端点移动的是一个区间,所以我们把所有不动的左端点上记录一下右端点移动的区间即可,由于不动的左端点只有可能是查询区间的左端点,所以这里空间复杂度降到$O ( n )$.

注意到我们求出的是两个查询的答案的差分,最后还需要做一下前缀和求答案.

二维分块

我们现在有一个需要维护的$n \times n$的平面,我们现在对其进行分块:

将平面分成$n^{ \frac{ 1 }{ 2 } }$个$n^{ \frac{ 3 }{ 4 } } \times n^{ \frac{ 3 }{ 4 } }$的$A$块,以$A$块为单位做二维前缀和.
每个$A$块内部分成$n^{ \frac{ 1 }{ 2 } }$个$n^{ \frac{ 1 }{ 2 } } \times n^{ \frac{ 1 }{ 2 } }$的$B$块,在$A$块内部以$B$块为单位做二维前缀和.
将整个平面横着分别分成一个个$n \times n^{ \frac{ 3 }{ 4 } }$的$C$块.(竖着也要分成一个个$n^{ \frac{ 3 }{ 4 } } \times n$的块,是类似的,略去)
每个$C$块内部分成$\sqrt{ n }$个$n^{ \frac{ 3 }{ 4 } } \times n^{ \frac{ 1 }{ 2 } }$个$D$块,在$C$块内部以$D$块为单位做二位前缀和.

注意到修改一个点的时候,需要更新三次二位前缀和,每次复杂度$O ( \sqrt{ n } )$.同时注意到空间复杂度是$O ( n )$的.

查询显然是分四种情况讨论:$A , B , D$块都可以快速求得答案,接下来只需要做一下散块就行.

那散块怎么做呢?我们考虑一个特殊情况:修改点的纵坐标以及横坐标两两不同,或至少一个坐标只对应$O ( 1 )$个点.

如果查询的时候,也仍然是满足查询的一个$l$对应$O ( 1 )$个$r$,我们就可以枚举一个点被哪些查询查到了散块,显然只有可能有$O ( \sqrt{ n } )$个查询,记录一下即可.这样就做到了$O ( \sqrt{ n } )$单点改,$O ( 1 )$查询.

如果我们一开始不做二维前缀和,就可以实现$O ( 1 )$单点改,那这种情况下如何实现$O ( \sqrt{ n } )$求和呢?首先还是可以$O ( \sqrt{ n } )$求出整块的和.

横着和竖着的散块相同,只讨论横着的.由于横着的散块高度$< n^{ \frac{ 1 }{ 2 } }$,我们就可以在每次查询的时候用$\sqrt{ n }$的复杂度枚举一遍横纵坐标在这个区间的点然后暴力判断即可,也可以$O ( \sqrt{ n } )$求散块.

Example1(luoguP7448 [Ynoi2007] rdiq)

首先注意到这个问题严格难于区间逆序对,想到二次离线莫队.

开始做二次离线,发现问题在于我们需要求出右端点移动的时候,找到新增了多少个本质不同的逆序对.设上一个和$a_r$颜色相同的点是$r ‘$,则显然新增的逆序对只可能出现在$[ r ‘ , r ]$中.

由于我们现在在保证左端点不动,于是我们考虑对于每种颜色,找到其在这个左端点后第一次出现的位置,并且只在这个位置贡献答案.这里其实已经可以扫描线了,套一下二次离线,把点扔到二位坐标系上.

现在问题在于,我们需要从$n \rightarrow 1$扫左端点,总共做$O ( n )$次单点修改,做$O ( n \sqrt{ n } )$次矩阵查询.

现在我们要查询的也就是左下角为$( r ‘ + 1 , a_r )$,右上角是$( r , \infty )$的矩阵.

这个东西其实已经可以做高维前缀和了.为了使答案更显然,我们令$rev ( x ) = n - x + 1$.然后将所有点的纵坐标$rev$掉,现在我们要查询的也就是左下角为$( r ‘ + 1 , 1 )$,右上角是$( r , rev ( a_r ) )$的矩阵,这玩意可以拆前缀和拆成形如左下角是$( 1 , 1 )$,右上角是$( i , rev ( a_i ) )$的矩阵.也就是说我们的$O ( n \sqrt{ n } )$次矩阵查询本质上只有$O ( n )$种.

拆到这里发现其实到这一步$a_r$和$a_{ r ‘ }$是否相等已经不重要了,可以用一下基数排序让他俩有一定的差异.

然后上二维分块.

Example2(luoguP8530 [Ynoi2003] 博丽灵梦)

首先自然的想法是拿莫队扫掉$[ l_1 , r_1 ]$这一维.

这样我们的问题转化为:每次插入/删除一个点,求一个类似区间颜色数的东西.

那么这个东西咋做呢?

首先我们考虑插入/删除的本质,把第二维$[ l_2 , r_2 ]$扔到二维平面上,那本质也就是需要寻找前驱后继,然后对一个矩形做加法,查询的时候单点查询,可以配个树套树解决这个问题.

有没有什么好办法?先考虑对矩形做加法然后单点查询这个操作看上去很蛋疼.我们考虑把它转化为单点加法矩形查询.这个做法比较显然:如果没有相同的只贡献一次的限制,我们就可以直接对于每个点$( a , a )$上加上一个相应的$b$,然后每次查询矩阵即可.但是有了限制怎么办呢?我们考虑在每两个相邻的点$A ( x_1 , x_1 )$和$B ( x_2 , x_2 )$之间的$( x_1 , x_2 )$上加上一个$- b$,不难发现这样就满足了条件.

分析一下我们现在需要做的东西:

莫队时查询一个点的前驱后继,这个操作就需要$O ( 1 )$完成.
$n \sqrt{ n }$次单点修改,这个操作需要$O ( 1 )$完成.
$n$次矩阵求和,这个操作需要在小于$O ( \sqrt{ n } )$的时间完成.

对于第一个问题,我们可能会想到用链表来解决.但问题在于链表难以支持插入操作.不过问题不大,我们有回滚莫队.这样就可以实现只删除不插入,解决了问题.

而后半部分是一个经典的二维分块.

简单来说,我们首先需要猜出时间复杂度为$O ( n \sqrt{ n } )$,然后用到莫队,然后用二维平面表示这个问题,发现直接做不太能做,想到一步转化,转化后的问题的一半可以直接套二维分快.最后想到前半部分可以用回滚莫队+链表解决.

trie树

Example1([2019zrtg十连测day1]set)

首先反应是扔到trie上然后异或就是打个tag,但是$+ 1$很难处理,因为它形如在trie上找到所有长度连续为$1$到叶子的链并且全部翻转,不过打一下tag应该也能做.

更简单的做法是,我们考虑从小到大插入数字.这样异或几乎没有影响,但是$+ 1$的话就相当于反转一条从根开始均为$1$的链,这个东西更为好做.

线段树

普通线段树

Example1(luoguP6780 [Ynoi2009] pmrllcsrms)

感觉这题比较厉害.

先扔做法:对$c$分块,这样答案就是块内和块间的最大值.对于每个块都可以用线段树维护最大值,然后最后再求$\max$.而对于块间如何做呢?

我们设$suf_i$为前一个块的后$i$个数之和,$pre_i$为后一个块的前$i$个数之和.注意到我们要求的就是$\max \{ suf_i + pre_j | i + j \leq c \}$.这个咋做呢?

你注意到这个$i + j \leq c$的限制非常的奇怪,我们如果想处理两个东西,自然想让这两个东西联系越紧密越好,但是这个联系就特别奇怪.但没关系,我们注意到如果用$j \rightarrow c - j + 1$的话,这个限制就转化为了$i + c - j + 1 \leq c$,也就是$i < j$,这个限制就可以放到线段树上维护了.

仔细思考这个过程:线段树只可以维护有大于小于的限制的两个数,而不能维护和区间长度有关的条件.但如果一个限制和区间长度有关,可能可以通过翻转之类的操作取消掉区间长度.

这个问题解决了,我们再回到一开始:为啥要对$c$分块?

一方面,题目中的$c$是给定的.另一方面,我们注意到我们需要维护一个和$c$有关的东西,而如果没有$c$,或者说$c = n$的时候,这个东西是好维护的:一般的区间最大子段和其实暗含了$c = n$的条件.考虑到这一点,对$c$分块就合情合理了.换句话说,分块其实有两种用途:一种是平衡暴力的复杂度:它可以让一些和块长有关的暴力复杂度降低.另一种用途是保证某个东西的合法性.

一个需要注意的事是,由于我们最后查询的是一个区间,所以对于块间的处理是需要处理区间的.不过我选择将$a [ l - 1 ]$和$a [ r + 1 ]$都加上一个极大值.

但是啊,但是.我们发现我们一开始是需要把块间做线段树的那个$maxn$设成$- \infty$的.如果这两个东西设成等大的$- \infty$,就会出现错误,为啥呢?

因为一开始这样会使得运算过程中有可能出现比$- \infty$还要小的数字,最底层的$maxn$有可能覆盖掉上面的.

线段树分治

大概就是用到了线段树结构进行操作,通常用来处理存在区间的问题.

之所以说它是线段树分治而不是一般的分治,是因为有的时候我们还可以利用线段树的结构.

Example1([2022qbxt国庆Day1]dottlebot)

注意到每个点其实只需要找到$[ i - r_i , i - 1 ]$和$[ i + 1 , i + r_i ]$这两段的最大值,设为$x$,则最后的答案就是$\max \{ a_i + x \}$.

思考这个过程,我们将$[ i - r_i , i - 1 ]$和$[ i + 1 , i + r_i ]$这两条线段以$a_i$的权值放到线段树上.具体地,我们在线段树的每个节点都开一个堆存储覆盖了这个节点区间的线段的权值.然后利用线段树求出每个区间的$a_i$的最大值,在节点处和堆中元素一起更新答案即可.

线段树上二分

Example1([2022qbxt国庆Day3]analysis)

考虑全局的和是$sum$,则我们要在这些数中找到一个分界点,使得左边的和大于等于$sum$,然后再考虑能不能将右边移动一个过去.

先把数据离散化,那么这就是一个值域线段树上二分的过程.

另外值得一提的是,考虑树状数组的形态也即线段树删去所有的右儿子,因此树状数组上也是可以二分的.

Example2

给定$a_i , b_i$,选定至多$k$个位置使这里的值为$a_i - b_i$,其它位置的值是$a_i$,最小化最大子段和.

考虑先二分再贪心:二分一个值,然后看如果需要使得答案小于等于这个值,最少需要用多少次操作.这个咋做呢?一个想法是,我先从左到右去扫一遍,然后每次如果当前最大后缀和大于二分的$mid$,我们就需要找一个位置使得把这个位置改掉后,最大后缀和最小.

首先来看这个为什么是正确的.考虑后面的最大后缀和是会继承前面的最大后缀和的,因此让当前局面最小一定更优秀,并且每个位置选中的代价是相等的,那自然要选择贡献最高的那个.

显然,如果选择一个改掉的话,我们需要求出$\min_{ k = 1 }^r \{ \max ( \max_{ i = k + 1 }^n \{ sum_{ i } \} , - b_k + \max_{ i = 1 }^k \{ sum_i \} ) \}$.注意改掉一个位置后要把它的$b$变成$0$.

那么什么样的$b$有可能是我们要选中的呢?显然可能被选中的$b$一定是一个单调下降的序列中的某个,因为同等大小,选后面一定更优秀.上面那个式子我们是难以快速维护的,但如果我把它改成:$\min_{ k = 1 }^r \{ \max ( \max_{ i = k + 1 }^n \{ sum_{ i } \} , - \max_{ i = k }^n \{ b_i \} + \max_{ i = 1 }^k \{ sum_i \} ) \}$,你会发现前者是一个单调不升的序列,后者是一个单调不降的序列,现在我们想要让它们的$\max$尽量小,这玩意显然可以做线段树二分.

上面那个东西也就是:

$\begin{aligned} & \min_{ k = 1 }^r \{ \max ( sufmax ( sum )_{ k + 1 } , - sufmax ( b )_k + premax ( sum )_k \} \\ = & \min_{ k = 1 }^r \{ \max ( sufmax ( sum )_{ k + 1 } , - \max ( sufmax ( b )_{ k + 1 } , b_k ) + premax ( sum )_k \} \\ \end{aligned}$

这样就可以在交界点更新答案.

另外,我们实际上更新答案会用到实际上找到的最小的$k$后面最大的$b$,这是为啥呢?首先这样的确是更优秀的解,而且我们发现,我们的确有可能找到更靠前的位置,如果往前的挪动不影响$sufmax ( b )$的话.那有没有可能跳出了这一段,来到了更靠后的地方呢?这显然也不会,因为我们只找到最后面第一个处于当前分段函数的$b$,这个$b$必然存在.如果它所在的sufmax和premax不一样,那么会是一个更优秀的解,压根不可能找到前面.

线段树合并

线段树维护矩阵乘法

吉司机线段树

李超线段树

珂朵莉树

Example1(luoguP8512 [Ynoi Easy Round 2021] TEST_152)

首先有经典套路:赋值操作有用的只有最后一次.

所以考虑扫描线,扫右端点的时候直接用珂朵莉树做.这样就剩下左端点的问题,因为有珂朵莉树,所以再开以时间为下标的数据结构就能处理.

猫树

KD-Tree

处理$K$维正交范围(给定$n$个有意义的点)在线修改查询的数据结构,是一棵二叉树.单次复杂度$O ( n^{ 1 - \frac{ 1 }{ k } } + \log n )$.(单调修改复杂度只是$O ( \log n )$)

离线情况下通常可以用cdq分治代替.

如果要支持动态插点,可以使用复杂度不正确的替罪羊树重构+kdtree.

1D-Tree

也就是线段树.

2D-Tree

建树的时候,对于每一维轮流考虑,每次考虑将这一维上的坐标的中位数的点(基准点)找到,左右分治下去(下一层要考虑另一维)处理.查询和修改都是类似的.

struct KD_tree{
int son[2];
int x,y;
int siz;
int f;
int l,r,u,d;
}tr[qwq<<1|1];
int cur[qwq<<1|1];
int clen;
struct P{
int x,y;
}p[qwq<<1|1];
bool cmpx(P a,P b){
return a.x<b.x;
}
bool cmpy(P a,P b){
return a.y<b.y;
}
ll mabs(ll x){
if(x>0)return x;
return -x;
}
void pushup(int cnt){
tr[cnt].l=tr[cnt].r=tr[cnt].x;
tr[cnt].d=tr[cnt].u=tr[cnt].y;
tr[cnt].siz=1;
if(tr[cnt].son[0]){
tr[cnt].l=std::min(tr[cnt].l,tr[tr[cnt].son[0]].l);
tr[cnt].r=std::max(tr[cnt].r,tr[tr[cnt].son[0]].r);
tr[cnt].d=std::min(tr[cnt].d,tr[tr[cnt].son[0]].d);
tr[cnt].u=std::max(tr[cnt].u,tr[tr[cnt].son[0]].u);
tr[cnt].siz+=tr[tr[cnt].son[0]].siz;
}
if(tr[cnt].son[1]){
tr[cnt].l=std::min(tr[cnt].l,tr[tr[cnt].son[1]].l);
tr[cnt].r=std::max(tr[cnt].r,tr[tr[cnt].son[1]].r);
tr[cnt].d=std::min(tr[cnt].d,tr[tr[cnt].son[1]].d);
tr[cnt].u=std::max(tr[cnt].u,tr[tr[cnt].son[1]].u);
tr[cnt].siz+=tr[tr[cnt].son[1]].siz;
}
return ;
}
inline ll dispp(int pa,int pb){
return 1ll*mabs(tr[pa].x-tr[pb].x)+1ll*mabs(tr[pa].y-tr[pb].y);
}
inline ll dispm(int po,int mat){
if(!mat)return 320051113;
ll d=0;
if(tr[po].x<tr[mat].l)d+=tr[mat].l-tr[po].x;
if(tr[po].x>tr[mat].r)d+=tr[po].x-tr[mat].r;
if(tr[po].y<tr[mat].d)d+=tr[mat].d-tr[po].y;
if(tr[po].y>tr[mat].u)d+=tr[po].y-tr[mat].u;
return d;
}
bool get_var(int l,int r){
double avx=0,avy=0;
for(int i=l;i<=r;++i){
avx+=p[i].x;avy+=p[i].y;
}
avx/=(r-l+1);avy/=(r-l+1);
double varx=0,vary=0;
for(int i=l;i<=r;++i){
varx+=1ll*(avx-p[i].x)*(avx-p[i].x);
vary+=1ll*(avy-p[i].y)*(avy-p[i].y);
}
return varx<vary;
}
int build(int l,int r){
if(l>r)return 0;
int mid=(l+r)>>1;
int cnt=cur[mid];
tr[cnt].f=get_var(l,r);
if(tr[cnt].f)std::nth_element(p+l,p+mid,p+r+1,cmpy);
else std::nth_element(p+l,p+mid,p+r+1,cmpx);
tr[cnt].x=p[mid].x;tr[cnt].y=p[mid].y;tr[cnt].siz=1;
tr[cnt].son[0]=build(l,mid-1);
tr[cnt].son[1]=build(mid+1,r);
pushup(cnt);
return cnt;
}

笛卡尔树

Example1([CFgym101613]Factor-free tree)

首先有一个自然的想法是随便找一个和整个区间都互质的数,然后把序列分成左右两端向下递归.对于一棵构造出来的二叉树,它的复杂度就是$\sum dep_u$,是可以被卡成$O ( n^2 )$的.

但我们考虑类似dsu on tree的做法,我们每次找到一个点,它将一个区间劈成了两部分,我们把小的那部分的贡献删去,然后做大的那部分.在递归过程中把大的那部分的贡献逐渐消磨掉.最后再做小的那部分,这样就类似于启发式合并的过程,复杂度就正确了.

Example2(23省选第一轮集训day5C)

注意到最小值的条件是容易满足的.

考虑枚举以每个点为最大值转移的区间,假设为$[ l , r ]$,这样会有:$[ l - 1 , i - 1 ] \rightarrow [ i , r ]$.注意到我们可以选择其中较短的区间来更新零一个区间或被另一个区间更新.

单调队列

Example(loj3151)

首先自然地,我们设$f_{ i , j }$表示前$i$个测试点已经分成了$j$段的方案数,然后做转移,复杂度$O ( T^2 S )$.

接下来咋优化咧?~~决策单调性!~~

嘶这题好像不满足决策单调性(这个故事也告诉我们不要看到$k$最短路就想决策单调性).

冷静一下,首先如果我把$[ l , r ]$分到一段里,那这一段的答案和啥有关?显然只和有多少个人在这段区间中没挂分有关.对于一个右端点$r$,我们不妨枚举有多少个人会在它所在的子任务挂分.显然,在左端点在一个区间内的时候,这个子任务会有一定的人挂分.而且随着现在右端点的移动,这个区间的左右端点都是单调不降的.那我们对于每种人数做单调队列维护即可.

树套树

解决矩阵修改+单点查询或单点修改+矩阵查询问题.

Example1

维护一个序列支持把$x$位置的值改为$y$或查询一个区间中小于$y$的数个数.

用树状数组维护平衡树,每次在树状数组上对应的节点修改即可.

Example2(Luogu4054 [JSOI2009]计数问题)

乍一看是动态三维问题.

相等维度是特殊的,我们开$100$个二维数据结构处理值不同的情况,这样就是二维.

数据结构常见套路

分开考虑

Example1(P6105 [Ynoi2010] y-fast trie)

考虑只有两种可能:

$x + y < C$,取$x + y$作为答案.
$x + y \geq C$,取$x + y - C$作为答案.

后者只需要取出最大的两个数即可,至于前者,考虑将所有数字分成两个集合,一个集合只在$[ 0 , \lceil \frac{ C }{ 2 } \rceil )$中,一个集合包含剩下的数字.对于第一个集合,我们只需要取出其中最大的两个数字就行.接下来的问题是怎么处理跨越两个集合的答案.考虑将每个点对应的答案配对,显然每个点能影响到的点是一段区间,删除时暴力修改.

另外,$x + y < C$也就是$x < C - y$,我们把第二个集合中的元素全部变成$C - y$后插入,只需最小化$C - x - y$,这个只需要维护最大的$x$和最小的$C - y$就行.

合并信息

lxl:这种问题主要需要解决三件事:标记对标记可合并,标记对值可合并,值与值可合并.

Example1([HNOI2011]括号修复 / [JSOI2011]括号序列)

注意到只要知道区间的最小前缀和以及区间的和,这个题就做完了.我们只需要维护这两件事.区间的和显然是好维护的,难以维护的是最小前缀和,我们来分开看每个操作:

替换:简单的.翻转:不太好做,尝试维护一下最小后缀和.反转:需要维护最大前缀和,进一步需要维护最大后缀和.

这样就可以更新答案了.

Example2(P4198 楼房重建)

左右维护单调栈合并,但这样复杂度肯定不对.

怎么办呢?我们可以用$O ( \log n )$的单次pushup操作,也就是维护一下每个节点所代表的区间的答案和最大值,不断递归右子树(或左子树)判断.

Example3(CF1017G)

设$w_i$为从上往下延伸到$i$这个点后,还能多往下延伸多少,一开始$w$都是$- 1$,每次操作会让$w + = 1$.树链剖分维护子段最大非空后缀和.

去除冗余信息

Example1(luoguP6617)

自然的想法是考虑找到每个点前面第一个和它之和为$w$的数字,但这样就炸了,因为每修改一个点可能要影响$O ( n )$个点的答案.

我们注意到一个事实:我们也可以找到每个点后面第一个和它之和为$w$的数字,而显然只有两个数互相匹配才可行.如果$i < j < k , ( i , j ) , ( i , k )$分别配对,那么显然$( i , k )$没有用.这样每个点只有$O ( 1 )$个匹配了.

set维护颜色

Example1(luoguP5278 算术天才⑨与等差数列)

首先考虑$k = 1$怎么做,显然找一下区间最大值和区间最小值,然后就只需要判断区间内有没有重复元素,经典套路:set维护颜色,这样可以处理出每个点上一个和它相同颜色的点,拿线段树维护它的最大值.

$k \ne 1$怎么办呢?考虑这只是相当于要判断一下这个区间内的数字是否在$\bmod k$意义下全部相等,维护差分数组的区间$\gcd$就行.

复杂度均摊

Example1(CF702F T-Shirts)

看到这个感觉很奇怪,想想好像也没有什么快速tag算法.

我们考虑对人建平衡树,然后按照顺序买衣服,每次找到所有能买这件衣服的人,显然是平衡树的某棵子树.但是,这棵子树在买完衣服后可能就不满足顺序了,那怎么办呢?能不能暴力重构一波?

事实上是可以的,对于一件价格为$q$的衣服,$[ 0 , q )$的人肯定买不了,$[ q , 2 q - 1 ]$的人买完后,手上的钱至少减半,我们暴力处理,至于$[ 2 q , + \infty )$,显然买完后不会对其形态有什么影响,打个tag.

Example2(uoj228)

一个自然的想法是暴力开根号,它会迅速缩短两个数之间的差.但可能也不能缩到$0$,那怎么办呢?当我们发现这个区间的最大值和最小值开根号后的差不变了,我们就把开根操作改成区间减法就行了.

loj6029是等价做法.

Example3(Luogu 4690 [Ynoi2016]镜中的昆虫)

维护每个点的颜色相同的前驱,单点修改的话就是简单树套树.

然后区间推平可以用颜色块均摊(同一个颜色块内只需要改开头元素,剩下的都是$pre [ i ] = i - 1$).

根号分治

Example1(luoguP7722 [Ynoi2007] tmpq)

这个题告诉我们一个故事:有的时候,有的条件可能真的没用.

直接把题目改成:每次修改$a , b , c$中的某个数,求.

Example2

对于一个数字$x$,每次随机在$[ 1 , x ]$中一个数$y$并令$x \leftarrow x \bmod y$,初始值为$n$,求期望几次能变成$0$.

注意到如果$y$很小就直接做,$y$很大的话$\lfloor \frac{ x }{ y } \rfloor$很小,暴力做数论分块.

Example3

给定一棵树,每次修改树上某个点的权值,或询问某个点周围的点的权值和.

度数大的点在修改的时候改,度数小的在询问的时候做.

Example4

给定序列,每次询问给出两个数字$x , y$,求最小的$| i - j |$满足$a_i = x , a_j = y$.

对于出现次数大的,处理出它和所有数字的答案.

如果$x , y$出现次数都少,就在做的时候直接归并.

Example5(SHOI2006 Homework)

首先对于$Y$很小的情况直接预处理就行,每次插入的时候更新答案.

对于$Y$很大的情况,$\frac{ n }{ Y }$一定很小,我们不断查询大于等于$kY$的最小元素即可,这个可以值域分块来根号平衡做到$O ( 1 )$查询,$O ( \sqrt{ n } )$单点修改.具体地,我们对每个块处理出大于等于这个块的最小的$X$,以及块内每个点后面最小的$X$(必须在块内),然后定位到$kY$的块.

Example6

给定$n , m$,以及序列$a$和长度为$n$的排列$y$,你需要回答$m$个询问.对每个询问,给定$l , r$,查询:

$\sum_{ i = 1 }^n \sum_{ j = i + 1 }^n [ a_i = a_j ] \prod_{ k = i }^j [ l \leq y_k \leq r ]$

注意到$y_i = i$的时候,这题等价于小Z的袜子.因此这题不会低于根号复杂度.轮流猜算法,猜到根号分治.

首先有一个性质:对于一对点$( x , y ) , a_x = a_y , \nexists x < z < y , a_z = a_x$,对于$( x , y )$这个区间内部的点,它们其实是可以缩起来的!(比赛的时候没想到呜呜)具体来说,我们只需要保留它们中最大的那个和最小的那个就行.

接下来,对于出现次数大于$\sqrt{ n }$的数字,它们最多只有$\sqrt{ n }$个,考虑莫队复杂度$O ( n \sqrt{ m } + m )$,因此我们可以对每个分别做莫队,总复杂度$O ( n \sqrt{ m } + m \sqrt{ n } )$,注意用基数排序,甚至不能用桶排.

对于出现次数小于$\sqrt{ n }$的数字,这些数字一共最多有$n$个,每个点暴力配对就有$O ( n \sqrt{ n } )$个点对,然后$O ( m )$次询问,用根号平衡做扫描线,这里复杂度$O ( n \sqrt{ n } + m \sqrt{ n } )$.

重链分治

Example1(Luogu5314 [Ynoi2011]ODT)

其实不是根号分治,但是差不多,扔这里了.

给一棵树,边权为$1$,支持把一条链上所有点加上$k$,或者查询距离一个点$< = 1$的所有点的点权$kth$.$n \leq 2 \times 10^5$.

每个点周围的点一共有三种可能:父亲,重儿子,轻儿子,特判重儿子和父亲,然后处理出所有轻儿子的情况,这个怎么做都能做(大不了把所有轻儿子全扔平衡树里),然后重链剖分的时候只会改$O ( \log n )$个轻儿子.

扫描线

一维扫描线

最经典的应用是对于一个$B$维的静态问题,我们可能可以用扫描线扫掉一维,让它变成一个$B - 1$维的动态问题.不过扫描线处理的时候可能需要是低$side$的问题,具体情况具体分析.

主席树通常就是解决强制在线不能处理扫描线的问题.

另外,通常认为时间也是一维,也就是即使是动态问题也一般是等价于对时间跑了扫描线.

二维扫描线

也就是莫队.

Example

Example1(CF1609F Interesting Sections)

首先枚举每个数的$popcount$,相当于每次将一些点标记为关键点,然后查询有多少个区间满足区间最大值和最小值都是关键点.

可以求出每个点$x$作为最大值的影响区间$[ l , r ]$,也就是如果一个区间左端点在$[ l , x ]$,右端点在$[ x , r ]$即可满足条件.我们考虑放入一个左下角坐标为$( l , x )$,右上角坐标为$( x , r )$的矩阵.最小值也是同理的,最后也就是求所有最大值矩阵和所有最小值矩阵的交.注意到如果两个点相同,我们规定一下在前面的更小,那么最大值矩阵两两不交,最小值矩阵也两两不交,就是一个最简单的扫描线问题了.

Example2(CF833E)

离散化,设$S = \{ l \} \cup \{ r \}$,考虑用$len_i$表示$i$节点及以前最多能有多少阳光.我们考虑用$len_{ i - 1 }$更新$len_i$,如果$[ i - 1 , i ]$没被覆盖,显然直接加上这段的长度.如果$[ i - 1 , i ]$被覆盖大于两次,那显然直接继承$len_{ i - 1 }$.

先考虑$[ i - 1 , i ]$被两朵云覆盖了怎么办,我们考虑用$h_{ j , k }$表示当前被且只被$j$和$k$共同覆盖的区间长度,不难发现$h_{ j , k }$有值的地方很少,用map.然后还要加上它们各自的贡献,用$g_j$表示当前被且只被$j$覆盖的区间长度,这样就可以计算答案.而这两个辅助数组也可以在判断$[ i - 1 , i ]$是被一朵云还是被两朵云覆盖的时候更新掉.

如果$[ i - 1 , i ]$被一朵云覆盖了怎么办呢?我们考虑把这朵云杀了,但我们还可能杀掉前面的某一朵云,假设为$k$,那么就有两种情况:要么这两朵云有交,要么无交.

先考虑无交的情况,这个时候答案显然是$g_j + g_k$,用线段树处理出当前代价和小于等于$C$的$k$的$g_k$的最大值就行.

再考虑有交的情况,答案应该为$g_j + g_k + h_{ j , k }$,我们在每次遇到$( j , k )$的时候都在对方那里打个tag就好,也就是对于每个$j$,处理出和它有交的云中$g_j + g_k + h_{ j , k }$的最大值.虽然这些值都会变,但是只会变大,因此可以处理.

那么怎么判断两朵云有交呢?我们不用判断两朵云是否有交,因为前者一定没有后者优秀.不过需要判断两朵云不能是同一朵,这个存一下次大值就可以解决.

这样就转移完了这个题,挺厉害的.

Example3(loj3489)

时间也是一维,扫序列维护时间,线段树二分就可以解决.

具体地,我们需要对每个询问找到这个询问前最近的队列为空的时刻,然后这个时刻后面的答案就可以直接拿前缀max二分,问题在于怎么求这个时刻.

这个时刻也是好求的,它一定是前缀的最小值(这个点一定清空了,这个点后面的数比它小,因此这个点变成$0$后那些数一定没清空).

Example4(luoguP7709 「Wdsr-2.7」八云蓝自动机 Ⅱ)

如果初始序列全为$0$:

倒着扫操作序列,维护当前还没有得到答案的询问,每次找到一个操作一定将整个区间的询问全部得知了答案.

不然不会做.

Example5(luogu3863)

仍然是个数据结构维护时间维,扫描线扫序列维的东西.

Example6(qoj6304)

考虑横纵坐标是对称的,因此我们只需要考虑两横一竖的情况和三条横的情况.

先做三条横,枚举中间的那个横的位置,剩了一段前缀和一段后缀需要覆盖,这个可以前后缀预处理.

然后是两横一竖,扫竖线,问题转化为动态加入删除区间,求当前用两个点覆盖所有区间的方案数,不妨设这两个点是$L < R$,自然有$L \leq \min \{ r_i \} , R \geq \max \{ l_i \}$,那么当我们确定$L$后,我们有$R \in [ \max \{ l_i \} , f ( L ) ]$.接下来我们考虑如何计算$f ( L )$.

注意到$L < l_i \Rightarrow R \leq r_i$,我们考虑将$l_i$这个点的权值设成$r_i$,那么我们要做的就是一个后缀最小值求和,用楼房重建.

莫队

回滚莫队

带修莫队

也就是维护三维的扫描线,根据KDT不难发现复杂度是$O ( nm^{ \frac{ 2 }{ 3 } } )$,$B = n^{ \frac{ 2 }{ 3 } }$,排序原则是$( ls , rs , t )$,复杂度算一算就知道是对的.

树上莫队

二次离线莫队

这个直接拿区间逆序对当例子记笔记好了.

如果我们用正常的莫队做区间逆序对,我们会得到带个$\log n$的复杂度:也就是每次扩展一个数,计算它对答案的贡献,这个是必须带$\log n$的,而且查询次数等价于移动次数,我们甚至不能用根号平衡.

那么怎么解决这个问题呢?我们现在无非是有$n \sqrt{ n }$次询问,每次询问$f ( l , r , r + 1 )$表示区间$[ l , r ]$对$r + 1$的逆序对贡献.考虑差分成$f ( 1 , r , r + 1 ) - f ( 1 , l - 1 , r + 1 )$,前者显然可以迅速求出.而后者的右端点需要移动$n$次,需要查询总共$n \sqrt{ n }$次,zhe’ge

Example

Example1([Ynoi2016]这是我自己的发明)

dfn将子树转序列,注意到换根无非是把一个序列拆成了两个序列,这是好做的.不过这玩意都$4 - side$了,但是有可减性,减成$2 - side$就能莫队了.

Example2([HNOI2016]大数)

区间子区间问题对于莫队是有一个套路的:即转化为二元组计数问题.

具体怎么做呢?首先这个题我们特判掉$p = 2$和$p = 5$的情况,这个只需要判断个位数就可以.然后我们考虑求每个点后缀代表的数字$\bmod p$的值,设为$suf_i$,假设存在两个点$l , r$满足$p | ( suf_l - suf_{ r + 1 } )$,那么$[ l , r ]$就是合法的,这是自然的,也就等价于$suf_l = suf_{ r + 1 }$,相当于要对满足$suf_l = suf_{ r + 1 }$的二元组$( l , r )$计数,这个是可以用莫队维护的.

Example3(luoguP3604 美好的每一天)

类似上面那个题,用哈希(其实就是将26个字母表示成26个二的幂次)然后异或起来,和上面的题就完全一样了,做二元组计数.

区间子区间问题

求有多少个子区间满足条件.

上二维平面,子区间所代表的$( l , r )$的点一定是在一条角平分线上的一个等腰直角三角形.

Example1(CF997E)

考虑转化为二维平面,$a_{ l , r } = maxn - minn - ( r - l )$,显然只需要找到为$0$的操作就行,这四个数可以转化为四个矩形加法,做扫描线.

另外这里的矩阵加法有$3 - side$的,但是可差分成$2 - side$.

时间倒流

Example1([2022qbxt国庆Day6]sgtbeats)

首先考虑:如果一个点被清空了多次,那么只有最后一次有意义.

删除操作很难做,考虑变成插入,然后就可以拿数据结构维护操作序列的后缀max,存一下每个点最后被清空的时间,然后处理即可.

Example2([WC2006]水管局长)

时间倒流,删边变加边,LCT做一下.

数据结构维护分段函数

Example1(CF1540D Inverse Inversions)

考虑对于一个数列怎么构造:假设只考虑前$k$个数,它们的取值是$[ 1 , k ]$,现在加入第$k + 1$个数,由于我们知道它是前缀第几小,所以我们可以直接将它设成这个值,然后将前面所有大于等于这个值的点全都$+ 1$,不难发现这一定是唯一构造.

那么我们现在要知道$p_i$是多少,根据上面的构造过程,首先将$p_i = a_i$,然后不断向后遍历,每遇到一个$a_j$,如果$a_j \leq p_i$,则把$p_i + = 1$.

我们将数列分块,设块长为$B$,那一个值经过一个块的时候最多加块长个$1$.也就是经过整块的时候是一个$B$段的分段函数.

考虑暴力求出这个分段函数,每次询问的时候直接二分,修改的时候考虑每个块维护一个线段树,线段树的区间表示这个区间对应的分段函数.这样单点修改复杂度是$\sum{ \cfrac{ B }{ 2^i } } = B$的,

于是最后复杂度为$O ( T ( B + \cfrac{ n }{ B } \log n ) )$,取$B = \sqrt{ n \log n }$即可.

根号平衡

根号平衡主要用到下面四个东西:

$O ( 1 )$单点加,$O ( \sqrt{ n } )$区间和:维护块内的和即可.
$O ( \sqrt{ n } )$单点加,$O ( 1 )$区间和:维护块内和块间的前缀和即可.
$O ( \sqrt{ n } )$区间加,$O ( 1 )$单点和:差分转化为$( 2 )$.当然打标记也是可以的.
$O ( 1 )$区间加,$O ( \sqrt{ n } )$单点和:差分转化为$( 1 )$.当然打标记也是可以的.

还有一些拓展的东西:

维护值域$O ( n )$的集合,支持$O ( 1 )$插入,$O ( \sqrt{ n } )$查询第$k$小:值域分块就可以.
维护值域$O ( n )$的集合,支持$O ( \sqrt{ n } )$插入,$O ( 1 )$查询第$k$小:值域分块,然后暴力改变每个点所属的块就行.

Example

Example1(区间众数)

首先分块,处理出$f_{ l , r }$表示块$[ l , r ]$的答案.这样每次只需要加入散块中的每个数并判断答案即可,由于判断每个数在区间出现次数是$\log n$的,因此复杂度$O ( n \sqrt{ n \log n } )$.

但是可以优化,我们设$mx$表示当前众数出现次数,注意到我们判断一个数字在区间中出现次数是否大于$mx$可以$O ( 1 )$判断(处理出这个数所有的出现位置),而如果遇到两个数需要对冲,显然$mx$增加总次数也不会超过$O ( \sqrt{ n } )$,因此做到$O ( n \sqrt{ n } )$.

不删除莫队也能做.

当然,如果只要求区间众数的出现次数,可以直接莫队.

Example2(CodeChef Chef and Churu)

首先发现函数是不会被修改的,因此考虑对函数分块,对于那些散着的函数肯定可以用一个$O ( 1 )$查询区间和,$O ( \sqrt{ n } )$单点修改的进行根号平衡.

而怎么快速处理整块呢?发现函数可差分,差分后就可以算出每一个位置对这个块内的总贡献,这样就可以更新了.

Example3([Ahoi2013]作业)

莫队,发现有$m$次查询,$n \sqrt{ m }$次移动,于是根号平衡.

Example4(Bzoj4241历史研究)

~~回滚莫队板子.~~

事实上考虑可能的答案只有$O ( n )$种,用值域分块就可以平衡复杂度.